Quantum dot cellular automaton
Encyclopedia
Quantum Dot Cellular Automata (sometimes referred to simply as quantum cellular automata
, or QCA) are proposed models of quantum computation, which have been devised in analogy to conventional models of cellular automata introduced by von Neumann.
, the latter implying the former. This means that such a device must have barriers that make it possible to distinguish between states, and that it must have the ability to control these barriers to perform conditional
change of state. For example, in a digital electronic system, transistors play the role of such controllable energy barriers, making it extremely practical to perform computing with them.
(CA) is a finite state machine
consisting of a uniform (finite or infinite) grid of cells. Each one of these cells can only be in one of a finite number of states at a discrete time. The state of each cell in this grid is determined by the state of its adjacent cells, also called the cell's "neighborhood." The most popular example of a cellular automaton was presented by John Horton Conway
in 1970, which he named "The Game of Life
."
cells. The automaton quickly gained popularity and it was first fabricated in 1997. Lent combined the discrete nature of both cellular automata and quantum mechanics
, to create nano-scale devices capable of performing computation at very high switching speeds and consuming extremely small amounts of electrical power.
QCA cell design considers the distance between quantum dot
s to be about 20 nm, and a distance between cells of about 60 nm. Just like any CA, Quantum (-dot) Cellular Automata are based on the simple interaction rules between cells placed on a grid. A QCA cell is constructed from four quantum dots arranged in a square pattern. These quantum dots are sites electrons can occupy by tunneling
to them.
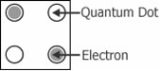
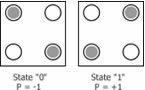Figure 2 shows a simplified diagram of a quantum-dot cell. If the cell is charged with two electrons, each free to tunnel to any site in the cell, these electrons will try to occupy the furthest possible site with respect to each other due to mutual electrostatic repulsion
. Therefore, two distinguishable cell states exist. Figure 3 shows the two possible minimum energy states
of a quantum-dot cell. The state of a QCA represents its polarization
, denoted as P. Although arbitrary in meaning, using cell polarization P = -1 to represent logic “0” and P = +1 to represent logic “1” has become standard practice.
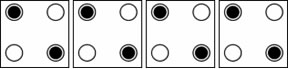Grid arrangements of quantum-dot cells behave in a ways that allow for computation. The simplest practical cell arrangement is given by placing quantum-dot cells in series
, to the side of each other. Figure 4 shows such an arrangement of four quantum-dot cells. The bounding boxes in the figure do not represent physical implementation, but are shown as means to identify individual cells.
If the polarization of any of the cells in the arrangement shown in figure 4 were to be controllable (driver cell), the rest of the cells would immediately synchronize to its polarization due to Coulombic interactions
between them; much like an instantaneous chain reaction. In this way, a wire of quantum-dot cells is realizable. Although the ability to realize conductive wires does not alone provide the means to perform computation, a complete set of universal logic gates can be constructed using the same principle.
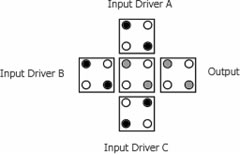The fundamental logic gate
in QCA is the majority gate. Figure 5 shows a majority gate with three inputs and one output. Assuming inputs A and B exist in a “binary 0” state and input C exists in a “binary 1” state, the output will exist in a “binary 0” state as the conjunct electrical field effect of inputs A and B is greater than the one of input C. In other words, the majority gate drives the output cell’s state to be equal to that of the majority of the inputs. Now, if the polarization of input C were to be fixed to say, binary 0, the only way the output’s state becomes binary 1, is if input A and B are also 1. Otherwise, the output cell will exhibit a binary 0 state.
. Similarly, an OR gate
can be constructed using a majority gate with fixed polarization equivalent to binary 1 at one of its inputs. In this way, if any or both of the remaining inputs exist in the binary 1 state, the output will be also in a binary 1 state. Although not certainly based on a majority gate structure, a NOT gate is just as easily realizable. The key principle behind its functionality lies on the fact that placing a cell at 45 degrees with respect of a pair of cells of same polarity, the polarization of the cell will become opposite to that of its driving pair. Figure 6 shows a standard implementation of a NOT logic gate.
There is a connection between quantum-dot cells and cellular automata. Cells can only be in one of 2 states and the conditional change of state in a cell is dictated by the state of its adjacent neighbors. However, a method to control data flow is necessary to define the direction in which state transition occurs in QCA cells. The clocks
of a QCA system serve two purposes: powering the automaton, and controlling data flow direction. QCA clocks are areas of conductive material under the automaton’s lattice
, modulating the electron tunneling barriers in the QCA cells above it.
Figure 7 shows a clock signal with its four stages and the effects on a cell at each clock stage. A typical QCA design requires four clocks, each of which is cyclically 90 degrees out of phase
with the prior clock. If a horizontal wire consisted of say, 8 cells and each consecutive pair, starting from the left were to be connected to each consecutive clock, data would naturally flow from left to right. The first pair of cells will stay latched until the second pair of cells gets latched and so forth. In this way, data flow direction is controllable through clock zones.
grid is doubled and an overall increase in geometric design complexity is inevitable. Yet another problem this technique presents is that the additional space between cells of the same orientation decreases the energy barriers between a cells ground state
and a cell’s first excited state
. This degrades the performance of the device in terms of maximum operating temperature, resistance to entropy
and switching speed.
, and Jeffrey D. Will, in their paper “Implementation of a crossbar network using quantum-dot cellular automata”. The paper not only presents a new method of implementing wire-crossings, but it also gives a new perspective on QCA clocking.
Their wire-crossing technique introduces the concept of implementing QCA devices capable of performing computation as a function of synchronization
. This implies the ability to modify the device’s function through the clocking system without making any physical changes to the device. Thus, the fabrication problem stated earlier is fully addressed by: a) using only one type of quantum-dot pattern and, b) by the ability to make a universal QCA building block of adequate complexity, which function is determined only by its timing mechanism (i.e. its clocks).
Quasi-adiabatic
switching, however, requires that the tunneling barriers of a cell be switched relatively slowly compared to the intrinsic switching speed of a QCA. This prevents ringing
and metastable
states observed when cells are switched abruptly. Therefore, the switching speed of a QCA is limited not by the time it takes for a cell to change polarization, but by the appropriate quasi-adiabatic switching time of the clocks being used.
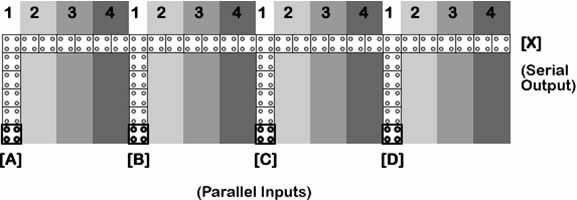
data stream
. This conversion allows different pieces of data to be reduced to a time-dependent series of values on a single wire. Figure 9 shows such a parallel-to-serial conversion QCA device. The numbers on the shaded areas represent different clocking zones at consecutive 90-degree phases. Notice how all the inputs are on the same clocking zone. If parallel data were to be driven at the inputs A, B, C and D, and then driven no more for at least the remaining 15 serial transmission phases, the output X would present the values of D, C, B and A –in that order, at phases three, seven, eleven and fifteen. If a new clocking region were to be added at the output, it could be clocked to latch a value corresponding to any of the inputs by correctly selecting an appropriate state-locking period.
The new latching clock region would be completely independent from the other four clocking zones illustrated in figure 9. For instance, if the value of interest to the new latching region were to be the value that D presents every 16th phase, the clocking mechanism of the new region would have to be configured to latch a value in the 4th phase and every 16th phase from then on, thus, ignoring all inputs but D.
This represents the flexibility to implement 16 functions, leaving the physical design untouched. Additional serial lines and parallel inputs would obviously increase the number of realizable functions. However, a significant drawback of such devices is that, as the number of realizable functions increases, an increasing number of clocking regions is required. As a consequence, a device exploiting this method of function implementation may perform significantly slower than its traditional counterpart.
(or solid state
) QCA implementations could potentially be used to implement QCA devices with the same highly advanced semiconductor fabrication
processes used to implement CMOS devices. Cell polarization is encoded as charge position, and quantum-dot interactions rely on electrostatic coupling. However, current semiconductor processes have not yet reached a point where mass production of devices with such small features (~20 nanometers) is possible. Serial lithographic
methods, however, make QCA solid state implementation achievable, but not necessarily practical. Serial lithography is slow, expensive and unsuitable for mass-production of solid-state QCA devices. Today, most QCA prototyping experiments are done using this implementation technology.
, and even the possibility of mass-producing devices by means of self-assembly. A number of technical challenges, including choice of molecules, the design of proper interfacing mechanisms, and clocking technology remain to be solved before this method can be implemented.
(CMOS) technology has been the industry standard for implementing Very Large Scale Integrated (VLSI) devices for the last two decades, mainly due to the consequences of miniaturization of such devices (i.e. increasing switching speeds, increasing complexity and decreasing power consumption). Quantum Cellular Automata (QCA) is only one of the many alternative technologies proposed as a replacement solution to the fundamental limits CMOS technology will impose in the years to come.
Although QCA solves most of the limitations of CMOS technology, it also brings its own. Research suggests that intrinsic switching time of a QCA cell is at best in the order of terahertz. However, the actual speed may be much lower, in the order of megahertz for solid state QCA and gigahertz for molecular QCA, due to the proper quasi-adiabatic clock switching frequency setting. Additionally, solid-state QCA devices cannot operate at room temperature. The only alternative to this temperature limitation is the recently proposed “Molecular QCA” which theoretically has an inter-dot distance of 2 nm and an inter-cell distance of 6 nm. Molecular QCA is also considered to be the only feasible implementation method for mass production of QCA devices.
Quantum cellular automata
Quantum Cellular Automata refers to models of quantum computation, which have been devised in analogy to conventional models of cellular automata introduced by von Neumann...
, or QCA) are proposed models of quantum computation, which have been devised in analogy to conventional models of cellular automata introduced by von Neumann.
Background
Any device designed to represent data and perform computation, regardless of the physics principles it exploits and materials used to build it, must have two fundamental properties: distinguishability and conditional change of stateState (computer science)
In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
, the latter implying the former. This means that such a device must have barriers that make it possible to distinguish between states, and that it must have the ability to control these barriers to perform conditional
Indicative conditional
In natural languages, an indicative conditional is the logical operation given by statements of the form "If A then B". Unlike the material conditional, an indicative conditional does not have a stipulated definition...
change of state. For example, in a digital electronic system, transistors play the role of such controllable energy barriers, making it extremely practical to perform computing with them.
Cellular automata
A cellular automatonCellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
(CA) is a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
consisting of a uniform (finite or infinite) grid of cells. Each one of these cells can only be in one of a finite number of states at a discrete time. The state of each cell in this grid is determined by the state of its adjacent cells, also called the cell's "neighborhood." The most popular example of a cellular automaton was presented by John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
in 1970, which he named "The Game of Life
Conway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
."
Origin
Cellular automata are commonly implemented as software programs. However, in 1993, Lent et al. proposed a physical implementation of an automaton using quantum-dotQuantum dot
A quantum dot is a portion of matter whose excitons are confined in all three spatial dimensions. Consequently, such materials have electronic properties intermediate between those of bulk semiconductors and those of discrete molecules. They were discovered at the beginning of the 1980s by Alexei...
cells. The automaton quickly gained popularity and it was first fabricated in 1997. Lent combined the discrete nature of both cellular automata and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, to create nano-scale devices capable of performing computation at very high switching speeds and consuming extremely small amounts of electrical power.
Modern cells
Today, standard solid stateSolid state (electronics)
Solid-state electronics are those circuits or devices built entirely from solid materials and in which the electrons, or other charge carriers, are confined entirely within the solid material...
QCA cell design considers the distance between quantum dot
Quantum dot
A quantum dot is a portion of matter whose excitons are confined in all three spatial dimensions. Consequently, such materials have electronic properties intermediate between those of bulk semiconductors and those of discrete molecules. They were discovered at the beginning of the 1980s by Alexei...
s to be about 20 nm, and a distance between cells of about 60 nm. Just like any CA, Quantum (-dot) Cellular Automata are based on the simple interaction rules between cells placed on a grid. A QCA cell is constructed from four quantum dots arranged in a square pattern. These quantum dots are sites electrons can occupy by tunneling
Quantum tunnelling
Quantum tunnelling refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important...
to them.
Theory behind cell
VSEPR theory
Valence shell electron pair repulsion theory is a model in chemistry used to predict the shape of individual molecules based upon the extent of electron-pair electrostatic repulsion. It is also named Gillespie–Nyholm theory after its two main developers...
. Therefore, two distinguishable cell states exist. Figure 3 shows the two possible minimum energy states
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
of a quantum-dot cell. The state of a QCA represents its polarization
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
, denoted as P. Although arbitrary in meaning, using cell polarization P = -1 to represent logic “0” and P = +1 to represent logic “1” has become standard practice.
Grid arrangements
Series and parallel circuits
Components of an electrical circuit or electronic circuit can be connected in many different ways. The two simplest of these are called series and parallel and occur very frequently. Components connected in series are connected along a single path, so the same current flows through all of the...
, to the side of each other. Figure 4 shows such an arrangement of four quantum-dot cells. The bounding boxes in the figure do not represent physical implementation, but are shown as means to identify individual cells.
If the polarization of any of the cells in the arrangement shown in figure 4 were to be controllable (driver cell), the rest of the cells would immediately synchronize to its polarization due to Coulombic interactions
Coulomb barrier
The Coulomb barrier, named after Coulomb's law, which is named after physicist Charles-Augustin de Coulomb , is the energy barrier due to electrostatic interaction that two nuclei need to overcome so they can get close enough to undergo a nuclear reaction...
between them; much like an instantaneous chain reaction. In this way, a wire of quantum-dot cells is realizable. Although the ability to realize conductive wires does not alone provide the means to perform computation, a complete set of universal logic gates can be constructed using the same principle.
Majority gate
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
in QCA is the majority gate. Figure 5 shows a majority gate with three inputs and one output. Assuming inputs A and B exist in a “binary 0” state and input C exists in a “binary 1” state, the output will exist in a “binary 0” state as the conjunct electrical field effect of inputs A and B is greater than the one of input C. In other words, the majority gate drives the output cell’s state to be equal to that of the majority of the inputs. Now, if the polarization of input C were to be fixed to say, binary 0, the only way the output’s state becomes binary 1, is if input A and B are also 1. Otherwise, the output cell will exhibit a binary 0 state.
Other gates
This conditional behavior is exactly the same as that of an AND gateAND gate
The AND gate is a basic digital logic gate that implements logical conjunction - it behaves according to the truth table to the right. A HIGH output results only if both the inputs to the AND gate are HIGH . If neither or only one input to the AND gate is HIGH, a LOW output results...
. Similarly, an OR gate
OR gate
The OR gate is a digital logic gate that implements logical disjunction - it behaves according to the truth table to the right. A HIGH output results if one or both the inputs to the gate are HIGH . If neither input is HIGH, a LOW output results...
can be constructed using a majority gate with fixed polarization equivalent to binary 1 at one of its inputs. In this way, if any or both of the remaining inputs exist in the binary 1 state, the output will be also in a binary 1 state. Although not certainly based on a majority gate structure, a NOT gate is just as easily realizable. The key principle behind its functionality lies on the fact that placing a cell at 45 degrees with respect of a pair of cells of same polarity, the polarization of the cell will become opposite to that of its driving pair. Figure 6 shows a standard implementation of a NOT logic gate.
State transition
Clock signal
In electronics and especially synchronous digital circuits, a clock signal is a particular type of signal that oscillates between a high and a low state and is utilized like a metronome to coordinate actions of circuits...
of a QCA system serve two purposes: powering the automaton, and controlling data flow direction. QCA clocks are areas of conductive material under the automaton’s lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, modulating the electron tunneling barriers in the QCA cells above it.
Four stages
A QCA clock induces four stages in the tunneling barriers of the cells above it. In the first stage, the tunneling barriers start to rise. The second stage is reached when the tunneling barriers are high enough to prevent electrons from tunneling. The third stage occurs when the high barrier starts to lower. And finally, in the fourth stage, the tunneling barriers allow electrons to freely tunnel again. In simple words, when the clock signal is high, electrons are free to tunnel. When the clock signal is low, the cell becomes latched.Figure 7 shows a clock signal with its four stages and the effects on a cell at each clock stage. A typical QCA design requires four clocks, each of which is cyclically 90 degrees out of phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
with the prior clock. If a horizontal wire consisted of say, 8 cells and each consecutive pair, starting from the left were to be connected to each consecutive clock, data would naturally flow from left to right. The first pair of cells will stay latched until the second pair of cells gets latched and so forth. In this way, data flow direction is controllable through clock zones.
Wire-crossing
Wire-crossing in QCA cells is done by using a "plus-sign" pattern, as shown in figure 8. The distances between a plus-sign pattern and a square pattern are exactly the same, allowing for the same Coulombic interactions between electrons in a cell. Thus, when a wire of square cells crosses a wire of plus-sign cells, they do not interact, thus the signals on each wire are preserved.Fabrication problem
Although this technique is rather simple, it represents an enormous fabrication problem. A new kind of cell pattern potentially introduces as much as twice the amount of fabrication cost and infrastructure; the number of possible quantum dot locations on an interstitialInterstitial
An interstitial space or interstice is an empty space or gap between spaces full of structure or matter.In particular, interstitial may refer to:-Physical sciences:...
grid is doubled and an overall increase in geometric design complexity is inevitable. Yet another problem this technique presents is that the additional space between cells of the same orientation decreases the energy barriers between a cells ground state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
and a cell’s first excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
. This degrades the performance of the device in terms of maximum operating temperature, resistance to entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
and switching speed.
Crossbar Network
A different wire-crossing technique, which makes fabrication of QCA devices more practical, was presented by Christopher Graunke, David Wheeler, Douglas TougawPaul Douglas Tougaw
Paul Douglas Tougaw, born July 3, 1969, is the chair of and a professor in the Department of Electrical and Computer Engineering at Valparaiso University. He received his B.S. in Electrical Engineering from the Rose-Hulmann Institute of Technology and his M.S. and Ph.D. in Electrical Engineering...
, and Jeffrey D. Will, in their paper “Implementation of a crossbar network using quantum-dot cellular automata”. The paper not only presents a new method of implementing wire-crossings, but it also gives a new perspective on QCA clocking.
Their wire-crossing technique introduces the concept of implementing QCA devices capable of performing computation as a function of synchronization
Synchronization (computer science)
In computer science, synchronization refers to one of two distinct but related concepts: synchronization of processes, and synchronization of data. Process synchronization refers to the idea that multiple processes are to join up or handshake at a certain point, so as to reach an agreement or...
. This implies the ability to modify the device’s function through the clocking system without making any physical changes to the device. Thus, the fabrication problem stated earlier is fully addressed by: a) using only one type of quantum-dot pattern and, b) by the ability to make a universal QCA building block of adequate complexity, which function is determined only by its timing mechanism (i.e. its clocks).
Quasi-adiabatic
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
switching, however, requires that the tunneling barriers of a cell be switched relatively slowly compared to the intrinsic switching speed of a QCA. This prevents ringing
Ringing (signal)
In electronics, signal processing, and video, ringing is unwanted oscillation of a signal, particularly in the step response...
and metastable
Metastability in electronics
Metastability in electronics is the ability of a digital electronic system to persist for an unbounded time in an unstable equilibrium or metastable state....
states observed when cells are switched abruptly. Therefore, the switching speed of a QCA is limited not by the time it takes for a cell to change polarization, but by the appropriate quasi-adiabatic switching time of the clocks being used.
Parallel to Serial
When designing a device capable of computing, it is often necessary to convert parallel data lines into a serialSerial communications
In telecommunication and computer science, serial communication is the process of sending data one bit at a time, sequentially, over a communication channel or computer bus. This is in contrast to parallel communication, where several bits are sent as a whole, on a link with several parallel channels...
data stream
Data stream
In telecommunications and computing, a data stream is a sequence of digitally encoded coherent signals used to transmit or receive information that is in the process of being transmitted....
. This conversion allows different pieces of data to be reduced to a time-dependent series of values on a single wire. Figure 9 shows such a parallel-to-serial conversion QCA device. The numbers on the shaded areas represent different clocking zones at consecutive 90-degree phases. Notice how all the inputs are on the same clocking zone. If parallel data were to be driven at the inputs A, B, C and D, and then driven no more for at least the remaining 15 serial transmission phases, the output X would present the values of D, C, B and A –in that order, at phases three, seven, eleven and fifteen. If a new clocking region were to be added at the output, it could be clocked to latch a value corresponding to any of the inputs by correctly selecting an appropriate state-locking period.
The new latching clock region would be completely independent from the other four clocking zones illustrated in figure 9. For instance, if the value of interest to the new latching region were to be the value that D presents every 16th phase, the clocking mechanism of the new region would have to be configured to latch a value in the 4th phase and every 16th phase from then on, thus, ignoring all inputs but D.
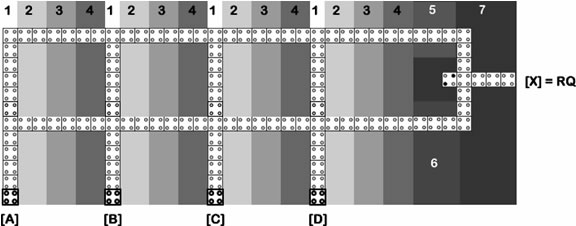
Additional serial lines
Adding a second serial line to the device, and adding another latching region would allow for the latching of two input values at the two different outputs. To perform computation, a gate that takes as inputs both serial lines at their respective outputs is added. The gate is placed over a new latching region configured to process data only when both latching regions at the end of the serial lines hold the values of interest at the same instant. Figure 10 shows such an arrangement. If correctly configured, latching regions 5 and 6 will each hold input values of interest to latching region 7. At this instant, latching region 7 will let the values latched on regions 5 and 6 through the AND gate, thus the output could be configured to be the AND result of any two inputs (i.e. R and Q) by merely configuring the latching regions 5, 6 and 7.This represents the flexibility to implement 16 functions, leaving the physical design untouched. Additional serial lines and parallel inputs would obviously increase the number of realizable functions. However, a significant drawback of such devices is that, as the number of realizable functions increases, an increasing number of clocking regions is required. As a consequence, a device exploiting this method of function implementation may perform significantly slower than its traditional counterpart.
Fabrication
Generally speaking, there are four different classes of QCA implementations: Metal-Island, Semiconductor, Molecular, and Magnetic.Metal-Island
The Metal-Island implementation was the first fabrication technology created to demonstrate the concept of QCA. It was not originally intended to compete with current technology in the sense of speed and practicality, as its structural properties are not suitable for scalable designs. The method consists of building quantum dots using aluminum islands. Earlier experiments were implemented with metal islands as big as 1 micrometer in dimension. Because of the relatively large-sized islands, Metal-Island devices had to be kept at extremely low temperatures for quantum effects (electron switching) to be observable.Semiconductor
SemiconductorSemiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
(or solid state
Solid state (electronics)
Solid-state electronics are those circuits or devices built entirely from solid materials and in which the electrons, or other charge carriers, are confined entirely within the solid material...
) QCA implementations could potentially be used to implement QCA devices with the same highly advanced semiconductor fabrication
Semiconductor fabrication
Semiconductor device fabrication is the process used to create the integrated circuits that are present in everyday electrical and electronic devices. It is a multiple-step sequence of photolithographic and chemical processing steps during which electronic circuits are gradually created on a wafer...
processes used to implement CMOS devices. Cell polarization is encoded as charge position, and quantum-dot interactions rely on electrostatic coupling. However, current semiconductor processes have not yet reached a point where mass production of devices with such small features (~20 nanometers) is possible. Serial lithographic
Electron beam lithography
Electron beam lithography is the practice of emitting a beam of electrons in a patterned fashion across a surface covered with a film , and of selectively removing either exposed or non-exposed regions of the resist...
methods, however, make QCA solid state implementation achievable, but not necessarily practical. Serial lithography is slow, expensive and unsuitable for mass-production of solid-state QCA devices. Today, most QCA prototyping experiments are done using this implementation technology.
Molecular
A proposed but not yet implemented method is method consists of building QCA devices out of single molecules. The main advantages of such implementations include: highly symmetric QCA cell structure, very high switching speeds, extremely high device density, operation at room temperatureRoom temperature
-Comfort levels:The American Society of Heating, Refrigerating and Air-Conditioning Engineers has listings for suggested temperatures and air flow rates in different types of buildings and different environmental circumstances. For example, a single office in a building has an occupancy ratio per...
, and even the possibility of mass-producing devices by means of self-assembly. A number of technical challenges, including choice of molecules, the design of proper interfacing mechanisms, and clocking technology remain to be solved before this method can be implemented.
Magnetic
Magnetic QCA –commonly referred to as MQCA (or QCA: M), is based on the interaction between magnetic nanoparticles. The magnetization vector of these nanoparticles is analogous to the polarization vector in all other implementations. In MQCA, the term “Quantum” refers to the quantum-mechanical nature of magnetic exchange interactions and not to the electron-tunneling effects. Devices constructed this way could operate at room temperature.Improvement over CMOS
Complementary metal-oxide semiconductorCMOS
Complementary metal–oxide–semiconductor is a technology for constructing integrated circuits. CMOS technology is used in microprocessors, microcontrollers, static RAM, and other digital logic circuits...
(CMOS) technology has been the industry standard for implementing Very Large Scale Integrated (VLSI) devices for the last two decades, mainly due to the consequences of miniaturization of such devices (i.e. increasing switching speeds, increasing complexity and decreasing power consumption). Quantum Cellular Automata (QCA) is only one of the many alternative technologies proposed as a replacement solution to the fundamental limits CMOS technology will impose in the years to come.
Although QCA solves most of the limitations of CMOS technology, it also brings its own. Research suggests that intrinsic switching time of a QCA cell is at best in the order of terahertz. However, the actual speed may be much lower, in the order of megahertz for solid state QCA and gigahertz for molecular QCA, due to the proper quasi-adiabatic clock switching frequency setting. Additionally, solid-state QCA devices cannot operate at room temperature. The only alternative to this temperature limitation is the recently proposed “Molecular QCA” which theoretically has an inter-dot distance of 2 nm and an inter-cell distance of 6 nm. Molecular QCA is also considered to be the only feasible implementation method for mass production of QCA devices.