
Quantum inequalities
Encyclopedia
Quantum inequalities are local constraints on the magnitude and extent of distributions of negative energy density in space-time. Initially conceived to clear up a long-standing problem in quantum field theory (namely, the potential for unconstrained negative energy density at a point), quantum inequalities have proven to have a diverse range of applications.
The form of the quantum inequalities is reminiscent of the uncertainty principle
.
amounts to a description of the relationship between the curvature of space-time, on the one hand, and the distribution of matter throughout space-time on the other. This precise details of this relationship are determined by the Einstein equations
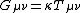 .
.
Here, the Einstein tensor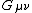 describes the curvature of space-time, whilst the energy-momentum tensor
describes the curvature of space-time, whilst the energy-momentum tensor 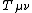 describes the local distribution of matter. (
describes the local distribution of matter. ( is a constant.) The Einstein equations express local relationships between the quantities involved—specifically, this is a system of coupled non-linear second order partial differential equations.
is a constant.) The Einstein equations express local relationships between the quantities involved—specifically, this is a system of coupled non-linear second order partial differential equations.
A very simple observation can be made at this point: the zero-point of energy-momentum is not arbitrary. Adding a "constant" to the right-hand side of the Einstein equations will effect a change in the Einstein tensor, and thus also in the curvature properties of space-time.
All known classical matter fields obey certain "energy condition
s". The most famous classical energy condition is the "weak energy condition"; this asserts that the local energy density, as measured by an observer moving along a time-like world line, is non-negative. The weak energy condition is essential for many of the most important and powerful results of classical relativity theory—in particular, the singularity theorems of Hawking et al.
is rather different: the expectation value of the energy density can be negative at any given point. In fact, things are even worse: by tuning the state of the quantum matter field, the expectation value of the local energy density can be made arbitrarily negative.
, and allow for several intrgiuing possibilities: for example, the Alcubierre drive
potentially allows for faster-than-light space travel.
Quantum inequalities constrain the magnitude and space-time extent of negative energy densities. In the case of the Alcubierre warp drive mentioned above, the quantum inequalities predict that the amount of exotic matter required to create and sustain the warp drive "bubble" far exceeds the total mass-energy of the universe.
More recently, Chris Fewster (of the University of York
, in the UK) has applied rigorous mathematics to produce a variety of quite general quantum inequalities. Collaborators have included Ford, Roman, Pfenning, Stefan Hollands and Rainer Verch.
http://www.phys.lsu.edu/mog/mog20/node16.html
Quantum Energy Inequalities (University of York, UK)
http://maths.york.ac.uk/www/PhysicsQIneq.htm
Phys. Rev. D 51 4277-4286
http://arxiv.org/abs/gr-qc/9410043
Fewster C J 2000 "A general worldline quantum inequality"
Class. Quant. Grav. 17 1897-1911
http://arxiv.org/abs/gr-qc/9910060
The form of the quantum inequalities is reminiscent of the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
.
Energy conditions in classical field theory
Einstein's theory of General RelativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
amounts to a description of the relationship between the curvature of space-time, on the one hand, and the distribution of matter throughout space-time on the other. This precise details of this relationship are determined by the Einstein equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
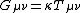 .
.Here, the Einstein tensor
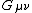 describes the curvature of space-time, whilst the energy-momentum tensor
describes the curvature of space-time, whilst the energy-momentum tensor 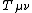 describes the local distribution of matter. (
describes the local distribution of matter. ( is a constant.) The Einstein equations express local relationships between the quantities involved—specifically, this is a system of coupled non-linear second order partial differential equations.
is a constant.) The Einstein equations express local relationships between the quantities involved—specifically, this is a system of coupled non-linear second order partial differential equations.A very simple observation can be made at this point: the zero-point of energy-momentum is not arbitrary. Adding a "constant" to the right-hand side of the Einstein equations will effect a change in the Einstein tensor, and thus also in the curvature properties of space-time.
All known classical matter fields obey certain "energy condition
Energy condition
In relativistic classical field theories of gravitation, particularly general relativity, an energy condition is one of various alternative conditions which can be applied to the matter content of the theory, when it is either not possible or desirable to specify this content explicitly...
s". The most famous classical energy condition is the "weak energy condition"; this asserts that the local energy density, as measured by an observer moving along a time-like world line, is non-negative. The weak energy condition is essential for many of the most important and powerful results of classical relativity theory—in particular, the singularity theorems of Hawking et al.
Energy conditions in quantum field theory
The situation in quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
is rather different: the expectation value of the energy density can be negative at any given point. In fact, things are even worse: by tuning the state of the quantum matter field, the expectation value of the local energy density can be made arbitrarily negative.
Applications
Distributions of negative energy density comprise what is often referred to as exotic matterExotic matter
In physics, exotic matter is a term which refers to matter which would somehow deviate from the norm and have "exotic" properties. There are several uses of the term....
, and allow for several intrgiuing possibilities: for example, the Alcubierre drive
Alcubierre drive
The Alcubierre drive, also known as the Alcubierre metric, is a speculative, but valid solution of the Einstein field equations. It is a mathematical model of a spacetime exhibiting features reminiscent of the fictional "warp drive" from Star Trek, which can travel "faster than light", although...
potentially allows for faster-than-light space travel.
Quantum inequalities constrain the magnitude and space-time extent of negative energy densities. In the case of the Alcubierre warp drive mentioned above, the quantum inequalities predict that the amount of exotic matter required to create and sustain the warp drive "bubble" far exceeds the total mass-energy of the universe.
People
The earliest investigations into quantum inequalities were carried out by Larry Ford and Tom Roman; an early collaborator was Mitch Pfenning, one of Ford's students at Tufts University. Important work was also carried out by Eanna Flanagan.More recently, Chris Fewster (of the University of York
University of York
The University of York , is an academic institution located in the city of York, England. Established in 1963, the campus university has expanded to more than thirty departments and centres, covering a wide range of subjects...
, in the UK) has applied rigorous mathematics to produce a variety of quite general quantum inequalities. Collaborators have included Ford, Roman, Pfenning, Stefan Hollands and Rainer Verch.
Websites
Quantum field theory on curved spacetime at the Erwin Schrödinger Institutehttp://www.phys.lsu.edu/mog/mog20/node16.html
Quantum Energy Inequalities (University of York, UK)
http://maths.york.ac.uk/www/PhysicsQIneq.htm
Papers
Ford L H and Roman T A 1995 "Averaged Energy Conditions and Quantum Inequalities"Phys. Rev. D 51 4277-4286
http://arxiv.org/abs/gr-qc/9410043
Fewster C J 2000 "A general worldline quantum inequality"
Class. Quant. Grav. 17 1897-1911
http://arxiv.org/abs/gr-qc/9910060

