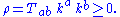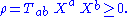Energy condition
Encyclopedia
In relativistic
classical field theories
of gravitation
, particularly general relativity
, an energy condition is one of various alternative conditions which can be applied to the matter content of the theory, when it is either not possible or desirable to specify this content explicitly. The hope is then that any reasonable matter theory will satisfy this condition or at least will preserve the condition if it is satisfied by the starting conditions.
In general relativity, energy conditions are often used (and required) in proofs of various important theorems about black holes, such as the no hair theorem
or the laws of black hole thermodynamics
.
and allied theories, the distribution of the mass, momentum, and stress due to matter and to any non-gravitational fields is described by the energy-momentum tensor (or matter tensor)
. However, the Einstein field equation is not very choosy about what kinds of states of matter or nongravitational fields are admissible in a spacetime model. This is both a strength, since a good general theory of gravitation should be maximally independent of any assumptions concerning nongravitational physics, and a weakness, because without some further criterion, the Einstein field equation admits putative solutions with properties most physicists regard as unphysical, i.e. too weird to resemble anything in the real universe even approximately.
The energy conditions represent such criteria. Roughly speaking, they crudely describe properties common to all (or almost all) states of matter and all nongravitational fields which are well-established in physics, while being sufficiently strong to rule out many unphysical "solutions" of the Einstein field equation. (It does not hold for matter described by a super-field, i.e., the Dirac field!)
Mathematically speaking, the most apparent distinguishing feature of the energy conditions is that they are essentially restrictions on the eigenvalues and eigenvectors of the matter tensor. A more subtle but no less important feature is that they are imposed eventwise, at the level of tangent space
s. Therefore they have no hope of ruling out objectionable global features, such as closed timelike curve
s.
s and the matter tensor.
First, a unit timelike vector field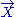
can be interpreted
as defining the world lines of some family of (possibly noninertial) ideal observers. Then the scalar field
can be interpreted as the total mass-energy density
(matter plus field energy of any nongravitational fields) measured by the observer from our family (at each event on his world line). Similarly, the vector field
with components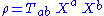
represents (after a projection) the momentum
measured by our observers.
Second, given an arbitrary null vector field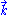
, the scalar field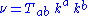
can be considered a kind of limiting case of the mass-energy density.
Third, in the case of general relativity, given an arbitrary timelike vector field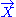
, again interpreted as describing the motion of a family of ideal observers, the Raychaudhuri scalar is the scalar field obtained by taking the trace
of the tidal tensor
corresponding to those observers at each event:
This quantity plays a crucial role in Raychaudhuri's equation. Then from Einstein field equation we immediately obtain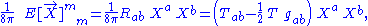
where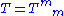
is the trace of the matter tensor.
,
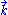Each of these has an averaged version, in which the properties noted above are to hold only on average along the flowlines of the appropriate vector fields. Otherwise, the Casimir effect
leads to exceptions. For example, the averaged null energy condition states that for every
flowline (integral curve)
of the null vector field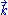 
, we must have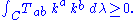
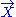, the matter density observed by the corresponding observers is always non-negative:
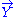, the vector field 
must be a future-pointing causal vector. That is, mass-energy can never be observed to be flowing faster than light.
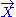, the trace of the tidal tensor measured by the corresponding observers is always non-negative:
The strong energy condition is hardly ever taken seriously nowadays because there are many matter configurations which violate it. For instance, a scalar field with a positive potential can violate this condition. Moreover, it is violated in any cosmological inflationary process.
Perfect fluids
possess a matter tensor of form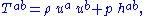
where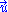
is the four-velocity
of the matter particles and where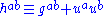
is the projection tensor onto the spatial hyperplane elements orthogonal to the four-velocity, at each event. (Notice that these hyperplane elements will not form a spatial hyperslice unless the velocity is vorticity-free; that is, irrotational.) With respect to a frame
aligned with the motion of the matter particles, the components of the matter tensor take the diagonal form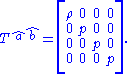
Here,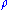
is the energy density
and
is the pressure
.
The energy conditions can then be reformulated in terms of these eigenvalues:
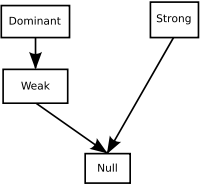
The implications among these conditions are indicated in the figure at right. Note that some of these conditions allow negative pressure. Also, note that despite the names the strong energy condition does not imply the weak energy condition even in the context of perfect fluids.
, in the region between two conducting plates held parallel at a very small separation d, there is a negative energy density
between the plates. (Be mindful, though, that the Casimir effect is topological, in that the sign of the vacuum energy depends on both the geometry and topology of the configuration. Being negative for parallel plates, the vacuum energy is positive for a conducting sphere.) Fortunately, various quantum inequalities
suggest that a suitable averaged energy condition may be satisfied in such cases. In particular, the averaged null energy condition is satisfied in the Casimir effect. Indeed, for energy-momentum tensors arising from effective field theories on Minkowski spacetime, the averaged null energy condition holds for everyday quantum fields. Extending these results is an open problem.
Observation of dark energy
, or the cosmological constant
, demonstrates that even the averaged strong energy condition must be false in cosmological solutions.
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
classical field theories
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, particularly general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, an energy condition is one of various alternative conditions which can be applied to the matter content of the theory, when it is either not possible or desirable to specify this content explicitly. The hope is then that any reasonable matter theory will satisfy this condition or at least will preserve the condition if it is satisfied by the starting conditions.
In general relativity, energy conditions are often used (and required) in proofs of various important theorems about black holes, such as the no hair theorem
No hair theorem
The no-hair theorem postulates that all black hole solutions of the Einstein-Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three externally observable classical parameters: mass, electric charge, and angular momentum...
or the laws of black hole thermodynamics
Black hole thermodynamics
In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
.
Motivation
In general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and allied theories, the distribution of the mass, momentum, and stress due to matter and to any non-gravitational fields is described by the energy-momentum tensor (or matter tensor)
. However, the Einstein field equation is not very choosy about what kinds of states of matter or nongravitational fields are admissible in a spacetime model. This is both a strength, since a good general theory of gravitation should be maximally independent of any assumptions concerning nongravitational physics, and a weakness, because without some further criterion, the Einstein field equation admits putative solutions with properties most physicists regard as unphysical, i.e. too weird to resemble anything in the real universe even approximately.The energy conditions represent such criteria. Roughly speaking, they crudely describe properties common to all (or almost all) states of matter and all nongravitational fields which are well-established in physics, while being sufficiently strong to rule out many unphysical "solutions" of the Einstein field equation. (It does not hold for matter described by a super-field, i.e., the Dirac field!)
Mathematically speaking, the most apparent distinguishing feature of the energy conditions is that they are essentially restrictions on the eigenvalues and eigenvectors of the matter tensor. A more subtle but no less important feature is that they are imposed eventwise, at the level of tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s. Therefore they have no hope of ruling out objectionable global features, such as closed timelike curve
Closed timelike curve
In mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s.
Some observable quantities
In order to understand the statements of the various energy conditions, one must be familiar with the physical interpretation of some scalar and vector quantities constructed from arbitrary timelike or null vectorNull vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
s and the matter tensor.
First, a unit timelike vector field
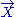can be interpretedCongruence (general relativity)
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
as defining the world lines of some family of (possibly noninertial) ideal observers. Then the scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
can be interpreted as the total mass-energy density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
(matter plus field energy of any nongravitational fields) measured by the observer from our family (at each event on his world line). Similarly, the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
with components
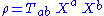represents (after a projection) the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
measured by our observers.
Second, given an arbitrary null vector field
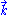, the scalar field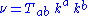can be considered a kind of limiting case of the mass-energy density.
Third, in the case of general relativity, given an arbitrary timelike vector field
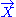, again interpreted as describing the motion of a family of ideal observers, the Raychaudhuri scalar is the scalar field obtained by taking the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the tidal tensor
Tidal tensor
In Newton's theory of gravitation and in various relativistic classical theories of gravitation, such as general relativity, the tidal tensor represents#tidal accelerations of a cloud of test particles,...
corresponding to those observers at each event:
This quantity plays a crucial role in Raychaudhuri's equation. Then from Einstein field equation we immediately obtain
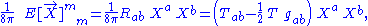
where
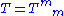is the trace of the matter tensor.Null energy condition
The null energy condition stipulates that for every future-pointing null vector field,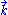
Each of these has an averaged version, in which the properties noted above are to hold only on average along the flowlines of the appropriate vector fields. Otherwise, the Casimir effect
Casimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
leads to exceptions. For example, the averaged null energy condition states that for every
flowline (integral curve)
of the null vector field 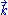, we must have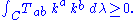Weak energy condition
The weak energy condition stipulates that for every future-pointing timelike vector field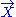, the matter density observed by the corresponding observers is always non-negative:
Dominant energy condition
The dominant energy condition stipulates that, in addition to the weak energy condition holding true, for every future-pointing causal vector field (either timelike or null)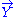, the vector field must be a future-pointing causal vector. That is, mass-energy can never be observed to be flowing faster than light.Strong energy condition
The strong energy condition stipulates that for every future-pointing timelike vector field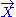, the trace of the tidal tensor measured by the corresponding observers is always non-negative:
The strong energy condition is hardly ever taken seriously nowadays because there are many matter configurations which violate it. For instance, a scalar field with a positive potential can violate this condition. Moreover, it is violated in any cosmological inflationary process.
Perfect fluids
Fluid solution
In general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
possess a matter tensor of form
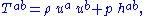
where
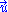is the four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
of the matter particles and where
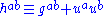is the projection tensor onto the spatial hyperplane elements orthogonal to the four-velocity, at each event. (Notice that these hyperplane elements will not form a spatial hyperslice unless the velocity is vorticity-free; that is, irrotational.) With respect to a frameFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
aligned with the motion of the matter particles, the components of the matter tensor take the diagonal form
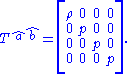
Here,
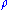is the energy densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and
is the pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
.
The energy conditions can then be reformulated in terms of these eigenvalues:
- The weak energy condition stipulates that
- The null energy condition stipulates that
- The strong energy condition stipulates that
- The dominant energy condition stipulates that
The implications among these conditions are indicated in the figure at right. Note that some of these conditions allow negative pressure. Also, note that despite the names the strong energy condition does not imply the weak energy condition even in the context of perfect fluids.
A counterexample
While the intent of the energy conditions is to provide simple criteria which rule out many unphysical situations while admitting any physically reasonable situation, in fact, at least when one introduces an effective field modeling some quantum mechanical effects, some possible matter tensors which are known to be physically reasonable and even realistic because they have been experimentally verified to actually fail various energy conditions. In particular, in the Casimir effectCasimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
, in the region between two conducting plates held parallel at a very small separation d, there is a negative energy density
between the plates. (Be mindful, though, that the Casimir effect is topological, in that the sign of the vacuum energy depends on both the geometry and topology of the configuration. Being negative for parallel plates, the vacuum energy is positive for a conducting sphere.) Fortunately, various quantum inequalities
Quantum inequalities
Quantum inequalities are local constraints on the magnitude and extent of distributions of negative energy density in space-time. Initially conceived to clear up a long-standing problem in quantum field theory , quantum inequalities have proven to have a diverse range of applications.The form of...
suggest that a suitable averaged energy condition may be satisfied in such cases. In particular, the averaged null energy condition is satisfied in the Casimir effect. Indeed, for energy-momentum tensors arising from effective field theories on Minkowski spacetime, the averaged null energy condition holds for everyday quantum fields. Extending these results is an open problem.
Observation of dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
, or the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
, demonstrates that even the averaged strong energy condition must be false in cosmological solutions.
See also
- Congruence (general relativity)Congruence (general relativity)In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime...
- Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
- Frame fields in general relativityFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...