Fluid solution
Encyclopedia
In general relativity
, a fluid solution is an exact solution
of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid
.
In astrophysics
, fluid solutions are often employed as stellar models. (It might help to think of a perfect gas as a special case of a perfect fluid.) In cosmology
, fluid solutions are often used as cosmological models.
of a relativistic fluid can be written in the form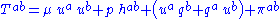
Here
The heat flux vector and viscous shear tensor are transverse to the world lines, in the sense that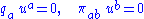
This means that they are effectively three-dimensional quantities, and since the viscous stress tensor is symmetric and traceless, they have respectively 3 and 5 linearly independent
components. Together with the density and pressure, this makes a total of 10 linearly independent components, which is the number of linearly independent components in a four-dimensional symmetric rank two tensor.
The last two are often used as cosmological models for (respectively) matter-dominated and radiation-dominated epochs. Notice that while in general it requires ten functions to specify a fluid, a perfect fluid requires only two, and dusts and radiation fluids each require only one function. It is much easier to find such solutions than it is to find a general fluid solution.
Among the perfect fluids other than dusts or radiation fluids, by far the most important special case is that of the static spherically symmetric perfect fluid
solutions. These can always be matched to a Schwarzschild vacuum
across a spherical surface, so they can be used as interior solutions in a stellar model. In such models, the sphere
where the fluid interior is matched to the vacuum exterior is the surface of the star, and the pressure must vanish in the limit as the radius approaches 
. However, the density can be nonzero in the limit from below, while of course it is zero in the limit from above. In recent years, several surprisingly simple schemes have been given for obtaining all these solutions.
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the special case of a perfect fluid, an adapted frame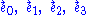
(the first is a timelike unit vector field
, the last three are spacelike unit vector fields)
can always be found in which the Einstein tensor takes the simple form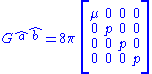
where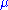
is the density and 
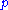is the pressure of the fluid. Here, the timelike unit vector field 
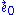is everywhere tangent to the world lines of observers who are comoving with the fluid elements, so the density and pressure just mentioned are those measured by comoving observers. These are the same quantities which appear in the general coordinate basis expression given in the preceding section; to see this, just put 
. From the form of the physical components, it is easy to see that the isotropy group of any perfect fluid is isomorphic to the three dimensional Lie group SO(3), the ordinary rotation group.
The fact that these results are exactly the same for curved spacetimes as for hydrodynamics in flat Minkowski spacetime is an expression of the equivalence principle
.
of the Einstein tensor in a perfect fluid must have the form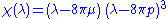
where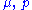
are again the density and pressure of the fluid as measured by observers comoving with the fluid elements. (Notice that these quantities can vary within the fluid.) Writing this out and applying Gröbner basis
methods to simplify the resulting algebraic relations, we find that the coefficients of the characteristic must satisfy the following two algebraically independent (and invariant) conditions: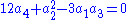
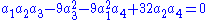
But according to Newton's identities
, the traces of the powers of the Einstein tensor are related to these coefficients as follows: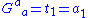
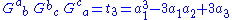
so we can rewrite the above two quantities entirely in terms of the traces of the powers. These are obviously scalar invariants, and they must vanish identically in the case of a perfect fluid solution:
Notice that this assumes nothing about any possible equation of state
relating the pressure and density of the fluid; we assume only that we have one simple and one triple eigenvalue.
In the case of a dust solution (vanishing pressure), these conditions simplify considerably:
or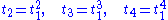
In tensor gymnastics notation, this can be written using the Ricci scalar as:
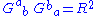
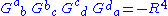
In the case of a radiation fluid, the criteria become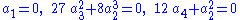
or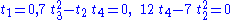
In using these criteria, one must be careful to ensure that the largest eigenvalue belongs to a timelike eigenvector, since there are Lorentzian manifolds, satisfying this eigenvalue criterion, in which the large eigenvalue belongs to a spacelike eigenvector, and these cannot represent radiation fluids.
The coefficients of the characteristic will often appear very complicated, and the traces are not much better; when looking for solutions it is almost always better to compute components of the Einstein tensor with respect to a suitably adapted frame and then to kill appropriate combinations of components directly. However, when no adapted frame is evident, these eigenvalue criteria can be sometimes be useful, especially when employed in conjunction with other considerations.
These criteria can often be useful for spot checking alleged perfect fluid solutions, in which case the coefficients of the characteristic are often much simpler than they would be for a simpler imperfect fluid.
s. Noteworthy perfect fluid solutions which feature positive pressure include various radiation fluid models from cosmology, including
In addition to the family of static spherically symmetric perfect fluids, noteworthy rotating fluid solutions include
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a fluid solution is an exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
.
In astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
, fluid solutions are often employed as stellar models. (It might help to think of a perfect gas as a special case of a perfect fluid.) In cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
, fluid solutions are often used as cosmological models.
Mathematical definition
The stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
of a relativistic fluid can be written in the form
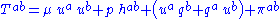
Here
- the world lines of the fluid elements are the integral curves of the velocity vectorFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
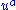, - the projection tensor
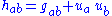projects other tensors onto hyperplane elements orthogonal to 
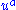, - the matter density is given by the scalar function
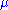, - the pressure is given by the scalar function
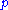, - the heat flux vector is given by
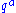, - the viscous shear tensor is given by
.
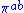The heat flux vector and viscous shear tensor are transverse to the world lines, in the sense that
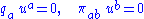
This means that they are effectively three-dimensional quantities, and since the viscous stress tensor is symmetric and traceless, they have respectively 3 and 5 linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
components. Together with the density and pressure, this makes a total of 10 linearly independent components, which is the number of linearly independent components in a four-dimensional symmetric rank two tensor.
Special cases
Several special cases of fluid solutions are noteworthy:- A perfect fluidPerfect fluidIn physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
has vanishing viscous shear and vanishing heat flux:
, - A dustDust solutionIn general relativity, a dust solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid which has positive mass density but vanishing pressure...
is a pressureless perfect fluid: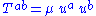
, - A radiation fluid is a perfect fluid with
:
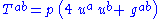
The last two are often used as cosmological models for (respectively) matter-dominated and radiation-dominated epochs. Notice that while in general it requires ten functions to specify a fluid, a perfect fluid requires only two, and dusts and radiation fluids each require only one function. It is much easier to find such solutions than it is to find a general fluid solution.
Among the perfect fluids other than dusts or radiation fluids, by far the most important special case is that of the static spherically symmetric perfect fluid
Static spherically symmetric perfect fluid
In metric theories of gravitation, particularly general relativity, a static spherically symmetric perfect fluid solution is a spacetime equipped with suitable tensor fields which models a static round ball of a fluid with isotropic pressure.Such solutions are often used as idealized models of...
solutions. These can always be matched to a Schwarzschild vacuum
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
across a spherical surface, so they can be used as interior solutions in a stellar model. In such models, the sphere
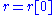where the fluid interior is matched to the vacuum exterior is the surface of the star, and the pressure must vanish in the limit as the radius approaches . However, the density can be nonzero in the limit from below, while of course it is zero in the limit from above. In recent years, several surprisingly simple schemes have been given for obtaining all these solutions.Einstein tensor
The components of a tensor computed with respect to a frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
rather than the coordinate basis are often called physical components, because these are the components which can (in principle) be measured by an observer.
In the special case of a perfect fluid, an adapted frame
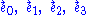
(the first is a timelike unit vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, the last three are spacelike unit vector fields)
can always be found in which the Einstein tensor takes the simple form
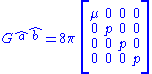
where
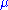is the density and 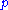is the pressure of the fluid. Here, the timelike unit vector field 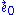is everywhere tangent to the world lines of observers who are comoving with the fluid elements, so the density and pressure just mentioned are those measured by comoving observers. These are the same quantities which appear in the general coordinate basis expression given in the preceding section; to see this, just put . From the form of the physical components, it is easy to see that the isotropy group of any perfect fluid is isomorphic to the three dimensional Lie group SO(3), the ordinary rotation group.The fact that these results are exactly the same for curved spacetimes as for hydrodynamics in flat Minkowski spacetime is an expression of the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
.
Eigenvalues
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Einstein tensor in a perfect fluid must have the form
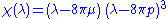
where
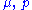are again the density and pressure of the fluid as measured by observers comoving with the fluid elements. (Notice that these quantities can vary within the fluid.) Writing this out and applying Gröbner basisGröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
methods to simplify the resulting algebraic relations, we find that the coefficients of the characteristic must satisfy the following two algebraically independent (and invariant) conditions:
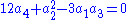
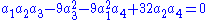
But according to Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, the traces of the powers of the Einstein tensor are related to these coefficients as follows:
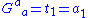
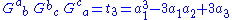
so we can rewrite the above two quantities entirely in terms of the traces of the powers. These are obviously scalar invariants, and they must vanish identically in the case of a perfect fluid solution:
Notice that this assumes nothing about any possible equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
relating the pressure and density of the fluid; we assume only that we have one simple and one triple eigenvalue.
In the case of a dust solution (vanishing pressure), these conditions simplify considerably:
or
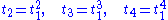
In tensor gymnastics notation, this can be written using the Ricci scalar as:
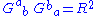
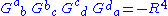
In the case of a radiation fluid, the criteria become
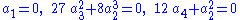
or
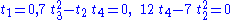
In using these criteria, one must be careful to ensure that the largest eigenvalue belongs to a timelike eigenvector, since there are Lorentzian manifolds, satisfying this eigenvalue criterion, in which the large eigenvalue belongs to a spacelike eigenvector, and these cannot represent radiation fluids.
The coefficients of the characteristic will often appear very complicated, and the traces are not much better; when looking for solutions it is almost always better to compute components of the Einstein tensor with respect to a suitably adapted frame and then to kill appropriate combinations of components directly. However, when no adapted frame is evident, these eigenvalue criteria can be sometimes be useful, especially when employed in conjunction with other considerations.
These criteria can often be useful for spot checking alleged perfect fluid solutions, in which case the coefficients of the characteristic are often much simpler than they would be for a simpler imperfect fluid.
Examples
Noteworthy individual dust solutions are listed in the article on dust solutionDust solution
In general relativity, a dust solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid which has positive mass density but vanishing pressure...
s. Noteworthy perfect fluid solutions which feature positive pressure include various radiation fluid models from cosmology, including
- FRW radiation fluids, often referred to as the radiation-dominated FRW models.
In addition to the family of static spherically symmetric perfect fluids, noteworthy rotating fluid solutions include
- Wahlquist fluid, which has similar symmetries to the Kerr vacuum, leading to initial hopes (since dashed) that it might provide the interior solution for a simple model of a rotating star.
See also
- Dust solutionDust solutionIn general relativity, a dust solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid which has positive mass density but vanishing pressure...
, for the important special case of dust solutions, - Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
, for exact solutions in general, - Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
- Perfect fluidPerfect fluidIn physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
, for perfect fluids in physics in general,