
Quasi-derivative
Encyclopedia
In mathematics
, the quasi-derivative is one of several generalizations of the derivative
of a function
between two Banach space
s. The quasi-derivative is a slightly stronger version of the Gâteaux derivative
, though weaker than the Fréchet derivative
.
Let f : A → F be a continuous function
from an open set
A in a Banach space E to another Banach space F. Then the quasi-derivative of f at x0 ∈ A is a linear transformation
u : E → F with the following property: for every continuous function g : [0,1] → A with g(0)=x0 such that g′(0) ∈ E exists,
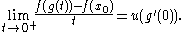
If such a linear map u exists, then f is said to be quasi-differentiable at x0.
Continuity of u need not be assumed, but it follows instead from the definition of the quasi-derivative. If f is Fréchet differentiable at x0, then by the chain rule
, f is also quasi-differentiable and its quasi-derivative is equal to its Fréchet derivative at x0. The converse is true provided E is finite dimensional. Finally, if f is quasi-differentiable, then it is Gâteaux differentiable and its Gâteaux derivative is equal to its quasi-derivative.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the quasi-derivative is one of several generalizations of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between two Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. The quasi-derivative is a slightly stronger version of the Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
, though weaker than the Fréchet derivative
Fréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
.
Let f : A → F be a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
from an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
A in a Banach space E to another Banach space F. Then the quasi-derivative of f at x0 ∈ A is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
u : E → F with the following property: for every continuous function g : [0,1] → A with g(0)=x0 such that g′(0) ∈ E exists,
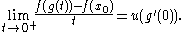
If such a linear map u exists, then f is said to be quasi-differentiable at x0.
Continuity of u need not be assumed, but it follows instead from the definition of the quasi-derivative. If f is Fréchet differentiable at x0, then by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, f is also quasi-differentiable and its quasi-derivative is equal to its Fréchet derivative at x0. The converse is true provided E is finite dimensional. Finally, if f is quasi-differentiable, then it is Gâteaux differentiable and its Gâteaux derivative is equal to its quasi-derivative.

