
Quasi-invariant measure
Encyclopedia
In mathematics
, a quasi-invariant measure μ with respect to a transformation T, from a measure space X to itself, is a measure
which, roughly speaking, is multiplied by a numerical function by T. An important class of examples occurs when X is a smooth manifold M, T is a diffeomorphism
of M, and μ is any measure that locally is a measure with base the Lebesgue measure
on Euclidean space
. Then the effect of T on μ is locally expressible as multiplication by the Jacobian determinant of the derivative (pushforward) of T.
To express this idea more formally in measure theory terms, the idea is that the Radon–Nikodym derivative of the transformed measure μ′ with respect to μ should exist everywhere; or that the two measures should be equivalent
(i.e. mutually absolutely continuous):
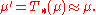
That means, in other words, that T preserves the concept of a set of measure zero. Considering the whole equivalence class of measures ν, equivalent to μ, it is also the same to say that T preserves the class as a whole, mapping any such measure to another such. Therefore the concept of quasi-invariant measure is the same as invariant measure class.
In general, the 'freedom' of moving within a measure class by multiplication gives rise to cocycle
s., when transformations are composed.
As an example, Gaussian measure
on Euclidean space
Rn is not invariant under translation (like Lebesgue measure is), but is quasi-invariant under all translations.
It can be shown that if E is a separable Banach space
and μ is a locally finite
Borel measure on E that is quasi-invariant under all translations by elements of E, then either dim(E) < +∞ or μ is the trivial measure
μ ≡ 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasi-invariant measure μ with respect to a transformation T, from a measure space X to itself, is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
which, roughly speaking, is multiplied by a numerical function by T. An important class of examples occurs when X is a smooth manifold M, T is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
of M, and μ is any measure that locally is a measure with base the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Then the effect of T on μ is locally expressible as multiplication by the Jacobian determinant of the derivative (pushforward) of T.
To express this idea more formally in measure theory terms, the idea is that the Radon–Nikodym derivative of the transformed measure μ′ with respect to μ should exist everywhere; or that the two measures should be equivalent
Equivalence (measure theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being "the same".-Definition:Let be a measurable space, and let μ, ν : Σ → R be two signed measures. Then μ is said to be equivalent to ν if and only if each is absolutely continuous with respect to the other...
(i.e. mutually absolutely continuous):
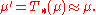
That means, in other words, that T preserves the concept of a set of measure zero. Considering the whole equivalence class of measures ν, equivalent to μ, it is also the same to say that T preserves the class as a whole, mapping any such measure to another such. Therefore the concept of quasi-invariant measure is the same as invariant measure class.
In general, the 'freedom' of moving within a measure class by multiplication gives rise to cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
s., when transformations are composed.
As an example, Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is not invariant under translation (like Lebesgue measure is), but is quasi-invariant under all translations.
It can be shown that if E is a separable Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and μ is a locally finite
Locally finite measure
In mathematics, a locally finite measure is a measure for which every point of the measure space has a neighbourhood of finite measure.-Definition:...
Borel measure on E that is quasi-invariant under all translations by elements of E, then either dim(E) < +∞ or μ is the trivial measure
Trivial measure
In mathematics, specifically in measure theory, the trivial measure on any measurable space is the measure μ which assigns zero measure to every measurable set: μ = 0 for all A in Σ.-Properties of the trivial measure:...
μ ≡ 0.

