
Quasivariety
Encyclopedia
In mathematics
, a quasivariety is a class of algebraic structure
s generalizing the notion of variety
by allowing equational conditions on the axioms defining the class.
satisfying any of the following equivalent conditions.
1. K is a pseudoelementary class
closed under subalgebras and direct products.
2. K is the class of all models of a set of quasiidentities, that is, implications of the form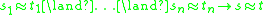 , where
, where 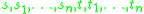 are term
are term
s built up from variables using the operation symbols of the specified signature.
3. K contains a trivial algebra and is closed under isomorphisms, subalgebras, and reduced product
s.
4. K contains a trivial algebra and is closed under isomorphisms, subalgebras, direct products, and ultraproduct
s.
is a quasivariety by virtue of an equation being a quasiidentity for which n = 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasivariety is a class of algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s generalizing the notion of variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
by allowing equational conditions on the axioms defining the class.
Definition
A trivial algebra contains just one element. A quasivariety is a class K of algebras with a specified signatureSignature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
satisfying any of the following equivalent conditions.
1. K is a pseudoelementary class
Pseudoelementary class
In logic, a pseudoelementary class is a class of structures derived from an elementary class by omitting some of its sorts and relations. It is the mathematical logic counterpart of the notion in category theory of a forgetful functor, and in physics of hidden variable theories purporting to...
closed under subalgebras and direct products.
2. K is the class of all models of a set of quasiidentities, that is, implications of the form
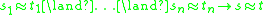 , where
, where 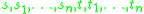 are term
are termTerm (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols...
s built up from variables using the operation symbols of the specified signature.
3. K contains a trivial algebra and is closed under isomorphisms, subalgebras, and reduced product
Reduced product
In model theory, a branch of mathematical logic, and in algebra, the reduced product is a construction that generalizes both direct product and ultraproduct....
s.
4. K contains a trivial algebra and is closed under isomorphisms, subalgebras, direct products, and ultraproduct
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
s.
Examples
Every varietyVariety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
is a quasivariety by virtue of an equation being a quasiidentity for which n = 0.

