In mathematics, a quintic threefold is a degree 5 dimension 3 hypersurface in 4-dimensional projective space. Non-singular quintic threefolds are Calabi-Yau manifold

Calabi-Yau manifold

A Calabi-Yau manifold is a special type of manifold that shows up in certain branches of mathematics such as algebraic geometry, as well as in theoretical physics...

s.

The Hodge diamond of a non-singular quintic 3-fold is

			1
		0		0
	0		1		0
1		101		101		1
	0		1		0
		0		0
			1

Rational curves

conjectured that the number of rational curves of a given degree on a generic quintic threefold is finite. (Some smooth but non-generic quintic threefolds have infinite families of lines on them.) This was verified for degrees up to 7 by who also calculated the number 609250 of degree 2 rational curves.

conjectured a general formula for the number of rational curves of any degree, which was proved by
The number of rational curves of various degrees on a generic quintic threefold is given by

5, 2875, 609250, 317206375, 242467530000, ....

Examples

• The Fermat quintic threefold
  Fermat quintic threefold
  In mathematics, a Fermat quintic threefold is a special quintic threefold, in other words a degree 5 dimension 3 hypersurface in 4-dimensional projective space, given byV^5+W^5+X^5+Y^5+Z^5=0...
  
   is given by .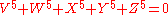
• Barth–Nieto quintic
  Barth–Nieto quintic
  In algebraic geometry, the Barth–Nieto quintic is a quintic 3-fold in 4 dimensional projective space studied by that is the Hessian of the Segre cubic...