Calabi-Yau manifold
Encyclopedia
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
that shows up in certain branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
such as algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, as well as in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
. Particularly in superstring theory
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
, the extra dimensions of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
are sometimes conjectured to take the form a 6-dimensional Calabi-Yau manifold.
Calabi–Yau manifolds are complex manifolds that are higher-dimensional analogues of K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s. They are sometimes defined as compact Kähler manifolds whose canonical bundle
Canonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
is trivial, though many other similar but inequivalent definitions are sometimes used. They were named "Calabi–Yau spaces" by after who first studied them, and who proved the Calabi conjecture
Calabi conjecture
In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by ....
that they have Ricci flat
Ricci-flat manifold
In mathematics, Ricci-flat manifolds are Riemannian manifolds whose Ricci curvature vanishes. In physics, they represent vacuum solutions to the analogues of Einstein's equations for Riemannian manifolds of any dimension, with vanishing cosmological constant...
metrics.
In superstring theory
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
the extra dimensions of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
are sometimes conjectured to take the form of a 6-dimensional Calabi–Yau manifold, which led to the idea of mirror symmetry.
Definitions
There are many different inequivalent definitions of a Calabi–Yau manifold used by different authors. This section summarizes some of the more common definitions and the relations between them.A Calabi–Yau n-fold or Calabi–Yau manifold of dimension n is sometimes defined as a compact n-dimensional Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
M satisfying one of the following equivalent conditions:
- The canonical bundleCanonical bundleIn mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
of M is trivial. - M has a holomorphic n-form that vanishes nowhere.
- The structure group of M can be reduced from U(n) to SU(n).
- M has a Kähler metric with global holonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
contained in SU(n).
These conditions imply that the first integral Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
c1(M) of M vanishes, but the converse is not true. The simplest examples where this happens are hyperelliptic surface
Hyperelliptic surface
In mathematics, a hyperelliptic surface, or bi-elliptic surface, is a surface with an elliptic fibration over an elliptic curve. Any such surface can be written as the quotient of a product of two elliptic curves by a finite abelian group....
s, finite quotients of a complex torus of complex dimension 2, which have vanishing first integral Chen class but the canonical bundle is not trivial.
For a compact n-dimensional Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
M the following conditions are equivalent to each other, but are weaker than the conditions above, and are sometimes used as the definition of a Calabi–Yau manifold:
- M has vanishing first real Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
. - M has a Kähler metric with vanishing Ricci curvatureRicci curvatureIn differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
. - M has a Kähler metric with local holonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
contained in SU(n). - A positive power of the canonical bundleCanonical bundleIn mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
of M is trivial. - M has a finite cover that has trivial canonical bundle.
- M has a finite cover that is a product of a torus and a simply connected manifold with trivial canonical bundle.
In particular if a compact Kähler manifold is simply connected then the weak definition above is equivalent to the stronger definition. Enriques surface
Enriques surface
In mathematics, Enriques surfaces, discovered by , are complex algebraic surfacessuch that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square...
s give examples of complex manifolds that have Ricci-flat metrics, but their canonical bundles are not trivial so they are Calabi–Yau manifolds according to the second but not the first definition above. Their double covers are Calabi–Yau manifolds for both definitions (in fact K3 surfaces).
By far the hardest part of proving the equivalences between the various properties above is proving the existence of Ricci-flat metrics. This follows from Yau's proof of the Calabi conjecture
Calabi conjecture
In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by ....
, which implies that a compact Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
with a vanishing first real Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
has a Kähler metric in the same class with vanishing Ricci curvature. (The class of a Kähler metric is the cohomology class of its associated 2-form.) Calabi showed such a metric is unique.
There are many other inequivalent definitions of Calabi–Yau manifolds that are sometimes used, which differ in the following ways (among others):
- The first Chern class may vanish as an integral class or as a real class.
- Most definitions assert that Calabi–Yau manifolds are compact, but some allow them to be non-compact. In the generalization to non-compact manifolds, the difference
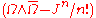must vanish asymptotically. Here, 
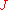is the Kähler form associated with the Kähler metric, 
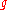. - Some definitions put restrictions on the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a Calabi–Yau manifold, such as demanding that it be finite or trivial. Any Calabi–Yau manifold has a finite cover that is the product of a torus and a simply-connected Calabi–Yau manifold. - Some definitions require that the holonomy be exactly equal to SU(n) rather than a subgroup of it, which implies that the Hodge numbers hi,0 vanish for 0 < i < dim(M). Abelian surfaces have a Ricci flat metric with holonomy strictly smaller than SU(2) (in fact trivial) so are not Calabi–Yau manifolds according to such definitions.
- Most definitions assume that a Calabi–Yau manifold has a Riemannian metric, but some treat them as complex manifolds without a metric.
- Most definitions assume the manifold is non-singular, but some allow mild singularities. While the Chern class fails to be well-defined for singular Calabi–Yau's, the canonical bundle and canonical class may still be defined if all the singularities are Gorenstein, and so may be used to extend the definition of a smooth Calabi–Yau manifold to a possibly singular Calabi–Yau variety.
Examples
In one complex dimension, the only compact examples are toriTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, which form a one-parameter family. The Ricci-flat metric on a torus is actually a flat metric, so that the holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
is the trivial group SU(1). A one-dimensional Calabi–Yau manifold is a complex elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
, and in particular, algebraic
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
In two complex dimensions, the K3 surface
K3 surface
In mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s furnish the only compact simply connected Calabi–Yau manifolds. Non simply-connected examples are given by abelian surface
Abelian surface
In mathematics, an abelian surface is 2-dimensional abelian variety.One dimensional complex tori are just elliptic curves and are all algebraic, but Riemann discovered that most complex tori of dimension 2 are not algebraic...
s. Enriques surface
Enriques surface
In mathematics, Enriques surfaces, discovered by , are complex algebraic surfacessuch that the irregularity q = 0 and the canonical line bundle K is non-trivial but has trivial square...
s and hyperelliptic surface
Hyperelliptic surface
In mathematics, a hyperelliptic surface, or bi-elliptic surface, is a surface with an elliptic fibration over an elliptic curve. Any such surface can be written as the quotient of a product of two elliptic curves by a finite abelian group....
s have first Chern class that vanishes as an element of the real cohomology group, but not as an element of the integral cohomology group, so Yau's theorem about the existence of a Ricci-flat metric still applies to them but they are sometimes not considered to be Calabi–Yau manifolds. Abelian surfaces are sometimes excluded from the classification of being Calabi–Yau, as their holonomy (again the trivial group) is a proper subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of SU(2), instead of being isomorphic to SU(2).
In three complex dimensions, classification of the possible Calabi–Yau manifolds is an open problem, although Yau suspects that there is a finite number of families (albeit a much bigger number than his estimate from 20 years ago). One example of a three-dimensional Calabi–Yau manifold is a non-singular quintic threefold
Quintic threefold
In mathematics, a quintic threefold is a degree 5 dimension 3 hypersurface in 4-dimensional projective space. Non-singular quintic threefolds are Calabi-Yau manifolds.The Hodge diamond of a non-singular quintic 3-fold is-Rational curves:...
in CP4
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, which is the algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
consisting of all of the zeros of a homogeneous quintic polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in the homogeneous coordinates of the CP4. Another example is a smooth model of the Barth–Nieto quintic
Barth–Nieto quintic
In algebraic geometry, the Barth–Nieto quintic is a quintic 3-fold in 4 dimensional projective space studied by that is the Hessian of the Segre cubic...
. Some discrete quotients of the quintic by various Z5 actions are also Calabi–Yau and have received a lot of attention in the literature. One of these is related to the original quintic by mirror symmetry
Mirror symmetry
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden...
.
For every positive integer n, the zero set of a non-singular homogeneous degree n+2 polynomial in the homogeneous coordinates of the complex projective space CPn+1 is a compact Calabi–Yau n-fold. The case n=1 describes an elliptic curve, while for n=2 one obtains a K3 surface.
All hyper-Kähler manifolds are Calabi–Yau.
Applications in superstring theory
Calabi–Yau manifolds are important in superstring theorySuperstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
. In the most conventional superstring models, ten conjectural dimensions in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
are supposed to come as four of which we are aware, carrying some kind of fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
with fiber dimension six. Compactification
Compactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
on Calabi–Yau n-folds are important because they leave some of the original supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
unbroken. More precisely, in the absence of fluxes, compactification on a Calabi–Yau 3-fold (real dimension 6) leaves one quarter of the original supersymmetry unbroken if the holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
is the full SU(3).
More generally, a flux-free compactification on an n-manifold with holonomy SU(n) leaves 21−n of the original supersymmetry unbroken, corresponding to 26−n supercharges in a compactification of type II supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
or 25−n supercharges in a compactification of type I. When fluxes are included the supersymmetry condition instead implies that the compactification manifold be a generalized Calabi–Yau, a notion introduced by . These models are known as flux compactifications.
Essentially, Calabi–Yau manifolds are shapes that satisfy the requirement of space for the six "unseen" spatial dimensions of string theory, which may be smaller than our currently observable lengths as they have not yet been detected. A popular alternative known as large extra dimension
Large extra dimension
In particle physics, models with universal extra dimensions propose that there are one or more additional dimensions beyond the three spatial dimensions and one temporal dimension that are observed...
s, which often occurs in braneworld models, is that the Calabi–Yau is large but we are confined to a small subset on which it intersects a D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
.
F-theory
F-theory
F-theory is a branch of string theory developed by Cumrun Vafa. The new vacua described as F-theory were discovered by Vafa, and it also allowed string theorists to construct new realistic vacua — in the form of F-theory compactified on elliptically fibered Calabi-Yau four-folds...
compactifications on various Calabi–Yau four-folds provide physicists with a method to find a large number of classical solution in the so-called string theory landscape
String theory landscape
The string theory landscape or anthropic landscape refers to the large number of possible false vacua in string theory. The "landscape" includes so many possible configurations that some physicists think that the known laws of physics, the standard model and general relativity with a positive...
.
External links
- Calabi–Yau Homepage is an interactive reference which describes many examples and classes of Calabi–Yau manifolds and also the physical theories in which they appear.
- Spinning Calabi–Yau Space video.
- Calabi–Yau Space by Andrew J. Hanson with additional contributions by Jeff Bryant, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. (similar to )