Radial set
Encyclopedia
In mathematics, given a linear space 
, a set 
is radial at the point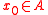 
if for every 
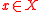there exists a 
such that for every 
, 
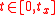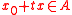. In set notation, 
is radial at the point 
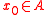if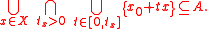
The set of all points at which
is radial is equal to the algebraic interior
.
A set
is absorbing
if and only if it is radial at 0.
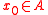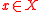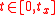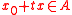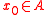, a set is radial at the point if for every there exists a such that for every , . In set notation, is radial at the point if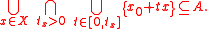The set of all points at which
is radial is equal to the algebraic interiorAlgebraic interior
In functional analysis, a branch of mathematics, the algebraic interior or radial kernel of a subset of a vector space is a refinement of the concept of the interior. It is the subset of points contained in a given set that it is absorbing with respect to, i.e...
.
A set
is absorbingAbsorbing set
In functional analysis and related areas of mathematics an absorbing set in a vector space is a set S which can be inflated to include any element of the vector space...
if and only if it is radial at 0.