
Radiosity
Encyclopedia

Global illumination
Global illumination is a general name for a group of algorithms used in 3D computer graphics that are meant to add more realistic lighting to 3D scenes...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used in 3D computer graphics
3D computer graphics
3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
rendering
Rendering (computer graphics)
Rendering is the process of generating an image from a model , by means of computer programs. A scene file contains objects in a strictly defined language or data structure; it would contain geometry, viewpoint, texture, lighting, and shading information as a description of the virtual scene...
. Radiosity is an application of the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
to solving the rendering equation
Rendering equation
In computer graphics, the rendering equation is an integral equation in which the equilibrium radiance leaving a point is given as the sum of emitted plus reflected radiance under a geometric optics approximation. It was simultaneously introduced into computer graphics by David Immel et al. and...
for scenes with purely diffuse surfaces. Unlike Monte Carlo algorithms
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
(such as path tracing
Path Tracing
Path tracing is a computer graphics rendering technique that attempts to simulate the physical behaviour of light as closely as possible. It is a generalisation of conventional ray tracing, tracing rays from the virtual camera through several bounces on or through objects...
) which handle all types of light paths, typical radiosity methods only account for paths which leave a light source and are reflected diffusely some number of times (possibly zero) before hitting the eye. Such paths are represented as "LD*E". Radiosity calculations are viewpoint independent which increases the computations involved, but makes them useful for all viewpoints.
Radiosity methods were first developed in about 1950 in the engineering field of heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
. They were later refined specifically for application to the problem of rendering computer graphics in 1984 by researchers at Cornell University
Cornell University
Cornell University is an Ivy League university located in Ithaca, New York, United States. It is a private land-grant university, receiving annual funding from the State of New York for certain educational missions...
.
Notable commercial radiosity engines are Enlighten by Geomerics
Geomerics
Geomerics is a software company based in Cambridge, UK, that specialises in creating lighting technology for the video game industry.The company's main product is Enlighten, software code that calculates indirect lighting in real time for live action games running on systems such as the...
, as seen in titles such as Battlefield 3, Need for Speed and others, Lightscape (now incorporated into the Autodesk
Autodesk
Autodesk, Inc. is an American multinational corporation that focuses on 3D design software for use in the architecture, engineering, construction, manufacturing, media and entertainment industries. The company was founded in 1982 by John Walker, a coauthor of the first versions of the company's...
3D Studio Max
3D Studio Max
Autodesk 3ds Max, formerly 3D Studio MAX, is for making 3D animations. It was developed and produced by Autodesk Media and Entertainment. It has modeling capabilities, a flexible plugin architecture and can be used on the Microsoft Windows platform. It's frequently used by video game developers, TV...
internal render engine), form•Z
Form-Z
form·Z is a computer-aided design tool developed by AutoDesSys for all design fields that deal with the articulation of 3D spaces and forms and which is used for 3D modeling, drafting, animation and rendering.-Overview:...
RenderZone Plus by AutoDesSys, Inc.), the built in render engine in LightWave 3D and ElAS
Electric Image Animation System
The Electric Image Animation System is a 3D computer graphics package published by EIAS3D. It currently runs on the Mac OS X and Windows platforms.-History:Electric Image, Inc. was initially a visual effects production company...
(Electric Image Animation System).
Visual characteristics

The image on the left was rendered with a typical direct illumination renderer. There are three types of lighting in this scene which have been specifically chosen and placed by the artist in an attempt to create realistic lighting: spot lighting with shadows (placed outside the window to create the light shining on the floor), ambient lighting (without which any part of the room not lit directly by a light source would be totally dark), and omnidirectional lighting without shadows (to reduce the flatness of the ambient lighting).
The image on the right was rendered using a radiosity algorithm. There is only one source of light: an image of the sky placed outside the window. The difference is marked. The room glows with light. Soft shadows are visible on the floor, and subtle lighting effects are noticeable around the room. Furthermore, the red color from the carpet has bled onto the grey walls, giving them a slightly warm appearance. None of these effects were specifically chosen or designed by the artist.
Overview of the radiosity algorithm
The surfaces of the scene to be rendered are each divided up into one or more smaller surfaces (patches).A view factor is computed for each pair of patches. View factors (also known as form factors) are coefficients describing how well the patches
can see each other. Patches that are far away from each other, or oriented at oblique angles relative to one another,
will have smaller view factors. If other patches are in the way, the view factor will be reduced or zero, depending
on whether the occlusion is partial or total.
The view factors are used as coefficients in a linearized form of the rendering equation, which yields
a linear system of equations. Solving this system yields the radiosity, or brightness, of each patch,
taking into account diffuse interreflections and soft shadows.
Progressive radiosity solves the system iteratively in such a way that after each iteration we have intermediate
radiosity values for the patch. These intermediate values correspond to bounce levels. That is, after one iteration,
we know how the scene looks after one light bounce, after two passes, two bounces, and so forth. Progressive radiosity
is useful for getting an interactive preview of the scene. Also, the user can stop the iterations once the image looks good
enough, rather than wait for the computation to numerically converge.

Mathematical formulation
The basic radiosity method has its basis in the theory of thermal radiationHeat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
, since radiosity relies on computing the amount of light energy transferred among surfaces. In order to simplify computations, the method assumes that all scattering is perfectly diffuse
Lambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
. Surfaces are typically discretized into quadrilateral or triangular elements
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
over which a piecewise polynomial function is defined.
After this breakdown, the amount of light energy transfer can be computed by using the known reflectivity of the reflecting patch, combined with the view factor of the two patches. This dimensionless quantity is computed from the geometric orientation of two patches, and can be thought of as the fraction of the total possible emitting area of the first patch which is covered by the second patch.
More correctly, radiosity B is the energy per unit area leaving the patch surface per discrete time interval and is the combination of emitted and reflected energy:

where:
- B(x)i dAi is the total energy leaving a small area dAi around a point x.
- E(x)i dAi is the emitted energy.
- ρ(x) is the reflectivity of the point, giving reflected energy per unit area by multiplying by the incident energy per unit area (the total energy which arrives from other patches).
- S denotes that the integration variable x' runs over all the surfaces in the scene
- r is the distance between x and x'
- θx and θx' are the angles between the line joining x and x' and vectors normal to the surface at x and x' respectively.
- Vis(x,x' ) is a visibility function, defined to be 1 if the two points x and x' are visible from each other, and 0 if they are not.
If the surfaces are approximated by a finite number of planar patches, each of which is taken to have a constant radiosity Bi and reflectivity ρi, the above equation gives the discrete radiosity equation,

where Fij is the geometrical view factor for the radiation leaving j and hitting patch i.
This equation can then be applied to each patch. The equation is monochromatic, so color radiosity rendering requires calculation for each of the required colors.
Solution methods
The equation can formally be solved as matrix equation, to give the vector solution: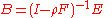
This gives the full "infinite bounce" solution for B directly. However the number of calculations to compute the matrix solution scales according to n3, where n is the number of patches. This becomes prohibitive for realistically large values of n.
Instead, the equation can more readily be solved iteratively, by repeatedly applying the single-bounce update formula above. Formally, this is a solution of the matrix equation by Jacobi iteration. Because the reflectivities ρi are less than 1, this scheme converges quickly, typically requiring only a handful of iterations to produce a reasonable solution. Other standard iterative methods for matrix equation solutions can also be used, for example the Gauss–Seidel method, where updated values for each patch are used in the calculation as soon as they are computed, rather than all being updated synchronously at the end of each sweep. The solution can also be tweaked to iterate over each of the sending elements in turn in its main outermost loop for each update, rather than each of the receiving patches. This is known as the shooting variant of the algorithm, as opposed to the gathering variant. Using the view factor reciprocity, Ai Fij = Aj Fji, the update equation can also be re-written in terms of the view factor Fji seen by each sending patch Aj:
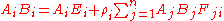
This is sometimes known as the "power" formulation, since it is now the total transmitted power of each element that is being updated, rather than its radiosity.
The view factor Fij itself can be calculated in a number of ways. Early methods used a hemicube (an imaginary cube centered upon the first surface to which the second surface was projected, devised by Cohen and Greenberg in 1985). The surface of the hemicube was divided into pixel-like squares, for each of which a view factor can be readily calculated analytically. The full form factor could then be approximated by adding up the contribution from each of the pixel-like squares. The projection onto the hemicube, which could be adapted from standard methods for determining the visibility of polygons, also solved the problem of intervening patches partially obscuring those behind.
However all this was quite computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
ally expensive, because ideally form factors must be derived for every possible pair of patches, leading to a quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
increase in computation as the number of patches increased. This can be reduced somewhat by using a binary space partitioning tree
Binary space partitioning
In computer science, binary space partitioning is a method for recursively subdividing a space into convex sets by hyperplanes. This subdivision gives rise to a representation of the scene by means of a tree data structure known as a BSP tree.Originally, this approach was proposed in 3D computer...
to reduce the amount of time spent determining which patches are completely hidden from others in complex scenes; but even so, the time spent to determine the form factor still typically scales as n log n. New methods include adaptive integration
Sampling approaches
The form factors Fij themselves are not in fact explicitly needed in either of the update equations; neither to estimate the total intensity ∑j Fij Bj gathered from the whole view, nor to estimate how the power Aj Bj being radiated is distributed. Instead, these updates can be estimated by sampling methods, without ever having to calculate form factors explicitly. Since the mid 1990s such sampling approaches have been the methods most predominantly used for practical radiosity calculations.The gathered intensity can be estimated by generating a set of samples in the unit circle, lifting these onto the hemisphere, and then seeing what was the radiosity of the element that a ray incoming in that direction would have originated on. The estimate for the total gathered intensity is then just the average of the radiosities discovered by each ray. Similarly, in the power formulation, power can be distributed by generating a set of rays from the radiating element in the same way, and spreading the power to be distributed equally between each element a ray hits.
This is essentially the same distribution that a path-tracing program would sample in tracing back one diffuse reflection step; or that a bidirectional ray tracing program would sample to achieve one forward diffuse reflection step when light source mapping forwards. The sampling approach therefore to some extent represents a convergence between the two techniques, the key difference remaining that the radiosity technique aims to build up a sufficiently accurate map of the radiance of all the surfaces in the scene, rather than just a representation of the current view.
Reducing computation time
Although in its basic form radiosity is assumed to have a quadratic increase in computation time with added geometry (surfaces and patches), this need not be the case. The radiosity problem can be rephrased as a problem of rendering a texture mappedTexture mapping
Texture mapping is a method for adding detail, surface texture , or color to a computer-generated graphic or 3D model. Its application to 3D graphics was pioneered by Dr Edwin Catmull in his Ph.D. thesis of 1974.-Texture mapping:...
scene. In this case, the computation time increases only linearly with the number of patches (ignoring complex issues like cache
Cache
In computer engineering, a cache is a component that transparently stores data so that future requests for that data can be served faster. The data that is stored within a cache might be values that have been computed earlier or duplicates of original values that are stored elsewhere...
use).
Following the commercial enthusiasm for radiosity-enhanced imagery, but prior to the standardization of rapid radiosity calculation, many architects and graphic artists used a technique referred to loosely as false radiosity
False radiosity
False Radiosity is a 3D computer graphics technique used to create texture mapping for objects that emulates patch interaction algorithms in radiosity rendering...
. By darkening areas of texture maps corresponding to corners, joints and recesses, and applying them via self-illumination or diffuse mapping, a radiosity-like effect of patch interaction could be created with a standard scanline renderer (cf. ambient occlusion
Ambient occlusion
Ambient occlusion is a shading method used in 3D computer graphics which helps add realism to local reflection models by taking into account attenuation of light due to occlusion...
).
Radiosity solutions may be displayed in realtime via Lightmaps
Lightmap
A lightmap is a data structure which contains the brightness of surfaces in 3d graphics applications such as video games. Lightmaps are precomputed and used for static objects. Quake was the first computer game to use lightmaps to augment rendering. Before lightmaps were invented, realtime...
on current desktop computers with standard graphics acceleration hardware
Advantages

Texture mapping
Texture mapping is a method for adding detail, surface texture , or color to a computer-generated graphic or 3D model. Its application to 3D graphics was pioneered by Dr Edwin Catmull in his Ph.D. thesis of 1974.-Texture mapping:...
, hidden surface removal) required to implement radiosity. A strong grasp of mathematics is not required to understand or implement this algorithm.
Limitations
Typical radiosity methods only account for light paths of the form LD*E, i.e., paths which start at a light source and make multiple diffuse bounces before reaching the eye. Although there are several approaches to integrating other illumination effects such as specularSpecular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
http://portal.acm.org/citation.cfm?id=37438&coll=portal&dl=ACM and glossy http://www.cs.huji.ac.il/labs/cglab/papers/clustering/ reflections, radiosity-based methods are generally not used to solve the complete rendering equation.
Basic radiosity also has trouble resolving sudden changes in visibility (e.g., hard-edged shadows) because coarse, regular discretization into piecewise constant elements corresponds to a low-pass box filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
of the spatial domain. Discontinuity meshing http://www.cs.cmu.edu/~ph/discon.ps.gz uses knowledge of visibility events to generate a more intelligent discretization.
Confusion about terminology
Radiosity was perhaps the first rendering algorithm in widespread use which accounted for diffuse indirect lighting. Earlier rendering algorithms, such as Whitted-style ray tracing were capable of computing effects such as reflections, refractions, and shadows, but despite being highly global phenomena, these effects were not commonly referred to as "global illumination." As a consequence, the term "global illumination" became confused with "diffuse interreflection," and "Radiosity" became confused with "global illumination" in popular parlance. However, the three are distinct concepts.The radiosity method in the current computer graphics context derives from (and is fundamentally the same as) the radiosity method in heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
. In this context radiosity
Radiosity (heat transfer)
Radiosity is a convenient quantity in optics and heat transfer that represents the total radiation intensity leaving a surface. Radiosity accounts for two components: the radiation being emitted by the surface, and the radiation being reflected from the surface...
is the total radiative flux (both reflected and re-radiated) leaving a surface, also sometimes known as radiant exitance. Calculation of Radiosity rather than surface temperatures is a key aspect of the radiosity method that permits linear matrix methods to be applied to the problem.
External links
- Radiosity Overview, from HyperGraph of SIGGRAPH (provides full matrix radiosity algorithm and progressive radiosity algorithm)
- Radiosity, by Hugo Elias (also provides a general overview of lighting algorithms, along with programming examples)
- Radiosity, by Allen Martin (a slightly more mathematical explanation of radiosity)
- RADical, by Parag Chaudhuri (an implementation of shooting & sorting variant of progressive radiosity algorithm with OpenGL acceleration, extending from GLUTRAD by Colbeck)
- ROVER, by Tralvex Yeap (Radiosity Abstracts & Bibliography Library)
- Radiosity Renderer and Visualizer (simple implementation of radiosity renderer based on OpenGLOpenGLOpenGL is a standard specification defining a cross-language, cross-platform API for writing applications that produce 2D and 3D computer graphics. The interface consists of over 250 different function calls which can be used to draw complex three-dimensional scenes from simple primitives. OpenGL...
) - Enlighten (Licensed software code that provides realtime radiosity for computer game applications. Developed by the UK company GeomericsGeomericsGeomerics is a software company based in Cambridge, UK, that specialises in creating lighting technology for the video game industry.The company's main product is Enlighten, software code that calculates indirect lighting in real time for live action games running on systems such as the...
)

