Rami Grossberg
Encyclopedia
Rami Grossberg is an associate professor of mathematics
at Carnegie Mellon University
and works in model theory
. Grossberg's recent work has revolved around the classification theory
of non-elementary classes, and is part of the active effort to prove two of Saharon Shelah
's outstanding categoricity conjecture
s:
Conjecture 1. (Categoricity for
). Let 
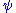be a sentence
. If
is categorical in a cardinal 
then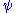 
is categorical in all cardinals 
. See Infinitary logic
and Beth number
.
Conjecture 2. (Categoricity for AECs) See http://www.math.cmu.edu/~rami/Rami-NBilgi.pdf and http://www2.math.uic.edu/~jbaldwin/pub/turino2.pdf. Let K be an AEC. There exists a cardinal μ(K) such that categoricity in a cardinal greater than μ(K) implies categoricity in all cardinals greater than μ(K). Furthemore, μ(K) is the Hanf number of K.
Examples of his results in pure model theory include: generalizing the Keisler–Shelah omitting types theorem for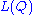
to successors of singular cardinals; with Shelah, introducing the notion of unsuper-stability for infinitary logics, and proving a nonstructure theorem, which is used to resolve a problem of Fuchs and Salce in the theory of modules; with Hart, proving a structure theorem for 
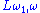, which resolves Morley's conjecture for excellent classes; and the notion of relative saturation and its connection to Shelah's conjecture for 
.
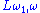Examples of his results in applications to algebra include the finding that under the weak continuum hypothesis
there is no universal object in the class of uncountable locally finite groups (answering a question of Macintyre and Shelah); with Shelah, showing that there is a jump in cardinality of the abelian group
Extp(G, Z) at the first singular strong limit cardinal; and, with Shelah, eliminating the use of the diamond in the proof of existence theorem for complete universal locally finite groups in several cardinalities.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
at Carnegie Mellon University
Carnegie Mellon University
Carnegie Mellon University is a private research university in Pittsburgh, Pennsylvania, United States....
and works in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. Grossberg's recent work has revolved around the classification theory
Classification theory
*For the practice and science of classification see Taxonomy and Library science* For the science of finding, describing and categorising organisms see alpha taxonomy*For classification theory in mathematical model theory see stable theory...
of non-elementary classes, and is part of the active effort to prove two of Saharon Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
's outstanding categoricity conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
s:
Conjecture 1. (Categoricity for
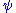). Let be a sentenceSentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
. If
is categorical in a cardinal then 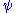is categorical in all cardinals . See Infinitary logicInfinitary logic
An infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
and Beth number
Beth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
.
Conjecture 2. (Categoricity for AECs) See http://www.math.cmu.edu/~rami/Rami-NBilgi.pdf and http://www2.math.uic.edu/~jbaldwin/pub/turino2.pdf. Let K be an AEC. There exists a cardinal μ(K) such that categoricity in a cardinal greater than μ(K) implies categoricity in all cardinals greater than μ(K). Furthemore, μ(K) is the Hanf number of K.
Examples of his results in pure model theory include: generalizing the Keisler–Shelah omitting types theorem for
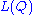to successors of singular cardinals; with Shelah, introducing the notion of unsuper-stability for infinitary logics, and proving a nonstructure theorem, which is used to resolve a problem of Fuchs and Salce in the theory of modules; with Hart, proving a structure theorem for 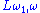, which resolves Morley's conjecture for excellent classes; and the notion of relative saturation and its connection to Shelah's conjecture for 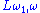.Examples of his results in applications to algebra include the finding that under the weak continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
there is no universal object in the class of uncountable locally finite groups (answering a question of Macintyre and Shelah); with Shelah, showing that there is a jump in cardinality of the abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Extp(G, Z) at the first singular strong limit cardinal; and, with Shelah, eliminating the use of the diamond in the proof of existence theorem for complete universal locally finite groups in several cardinalities.