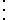Randomized block design
Encyclopedia
In the statistical theory of the design of experiments
, blocking
is the arranging of experimental units in groups (blocks) that are similar to one another. Typically, a blocking factor is a source of variability
that is not of primary interest to the experimenter. An example of a blocking factor might be the sex of a patient; by blocking on sex, this source of variability is controlled for, thus leading to greater accuracy.
.
Nuisance factors are those that may affect the measured result, but are not of primary interest. For example, in applying a treatment, nuisance factors might be the specific operator who prepared the treatment, the time of day the experiment was run, and the room temperature. All experiments have nuisance factors. The experimenter will typically need to spend some time deciding which nuisance factors are important enough to keep track of or control, if possible, during the experiment.
Blocking is used to remove the effects of a few of the most important nuisance variables. Randomization is then used to reduce the contaminating effects of the remaining nuisance variables.
experiments, each run within one of the blocks of the total experiment.
with
The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
An ideal way to run this experiment would be to run all the 4x3=12 wafers in the same furnace run. That would eliminate the nuisance furnace factor completely. However, regular production wafers have furnace priority, and only a few experimental wafers are allowed into any furnace run at the same time.
A non-blocked way to run this experiment would be to run each of the twelve experimental wafers, in random order, one per furnace run. That would increase the experimental error of each resistivity measurement by the run-to-run furnace variability and make it more difficult to study the effects of the different dosages. The blocked way to run this experiment, assuming you can convince manufacturing to let you put four experimental wafers in a furnace run, would be to put four wafers with different dosages in each of three furnace runs. The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4.
Before randomization, the design trials look like:
By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix.
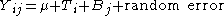
where
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, blocking
Blocking (statistics)
In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. For example, an experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male...
is the arranging of experimental units in groups (blocks) that are similar to one another. Typically, a blocking factor is a source of variability
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
that is not of primary interest to the experimenter. An example of a blocking factor might be the sex of a patient; by blocking on sex, this source of variability is controlled for, thus leading to greater accuracy.
Blocking to "remove" the effect of nuisance factors
For randomized block designs, there is one factor or variable that is of primary interest. However, there are also several other nuisance factorsNuisance variable
In statistics, a nuisance parameter is any parameter which is not of immediate interest but which must be accounted for in the analysis of those parameters which are of interest...
.
Nuisance factors are those that may affect the measured result, but are not of primary interest. For example, in applying a treatment, nuisance factors might be the specific operator who prepared the treatment, the time of day the experiment was run, and the room temperature. All experiments have nuisance factors. The experimenter will typically need to spend some time deciding which nuisance factors are important enough to keep track of or control, if possible, during the experiment.
Blocking used for nuisance factors that can be controlled
When we can control nuisance factors, an important technique known as blocking can be used to reduce or eliminate the contribution to experimental error contributed by nuisance factors. The basic concept is to create homogeneous blocks in which the nuisance factors are held constant and the factor of interest is allowed to vary. Within blocks, it is possible to assess the effect of different levels of the factor of interest without having to worry about variations due to changes of the block factors, which are accounted for in the analysis.Definition of blocking factors
A nuisance factor is used as a blocking factor if every level of the primary factor occurs the same number of times with each level of the nuisance factor. The analysis of the experiment will focus on the effect of varying levels of the primary factor within each block of the experiment.Block for a few of the most important nuisance factors
The general rule is:- "Block what you can, randomize what you cannot."
Blocking is used to remove the effects of a few of the most important nuisance variables. Randomization is then used to reduce the contaminating effects of the remaining nuisance variables.
Orientation of blocks when filtering extraneous gradients or variables
A general rule is to arrange blocks perpendicular to a gradient or extraneous variable; otherwise, filtering is inefficient and treatment effects are distorted. Refer to Mendenhall or Snedecor and Cochran. For methods of identifying or measuring a gradient and evaluating distortion, see randomized block theorem by Foos.Table of randomized block designs
One useful way to look at a randomized block experiment is to consider it as a collection of completely randomizedCompletely randomized design
In the design of experiments, completely randomized designs are for studying the effects of one primary factor without the need to take other nuisance variables into account. This article describes completely randomized designs that have one primary factor. The experiment compares the values of a...
experiments, each run within one of the blocks of the total experiment.
| Name of Design | Number of Factors k | Number of Runs n |
|---|---|---|
| 2-factor RBD | 2 | L1 * L2 |
| 3-factor RBD | 3 | L1 * L2 * L3 |
| 4-factor RBD | 4 | L1 * L2 * L3 * L4 |
 |
 |
 |
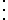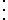| k-factor RBD | k | L1 * L2 *  * Lk |
with
- L1 = number of levels (settings) of factor 1
- L2 = number of levels (settings) of factor 2
- L3 = number of levels (settings) of factor 3
- L4 = number of levels (settings) of factor 4
- Lk = number of levels (settings) of factor k
Example of a Randomized Block Design
Suppose engineers at a semiconductor manufacturing facility want to test whether different wafer implant material dosages have a significant effect on resistivity measurements after a diffusion process taking place in a furnace. They have four different dosages they want to try and enough experimental wafers from the same lot to run three wafers at each of the dosages.The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
An ideal way to run this experiment would be to run all the 4x3=12 wafers in the same furnace run. That would eliminate the nuisance furnace factor completely. However, regular production wafers have furnace priority, and only a few experimental wafers are allowed into any furnace run at the same time.
A non-blocked way to run this experiment would be to run each of the twelve experimental wafers, in random order, one per furnace run. That would increase the experimental error of each resistivity measurement by the run-to-run furnace variability and make it more difficult to study the effects of the different dosages. The blocked way to run this experiment, assuming you can convince manufacturing to let you put four experimental wafers in a furnace run, would be to put four wafers with different dosages in each of three furnace runs. The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4.
Description of the experiment
Let X1 be dosage "level" and X2 be the blocking factor furnace run. Then the experiment can be described as follows:- k = 2 factors (1 primary factor X1 and 1 blocking factor X2)
- L1 = 4 levels of factor X1
- L2 = 3 levels of factor X2
- n = 1 replication per cell
- N = L1 * L2 = 4 * 3 = 12 runs
Before randomization, the design trials look like:
| X1 | X2 |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 1 | 3 |
| 2 | 1 |
| 2 | 2 |
| 2 | 3 |
| 3 | 1 |
| 3 | 2 |
| 3 | 3 |
| 4 | 1 |
| 4 | 2 |
| 4 | 3 |
Matrix Representation
An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above.By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix.
Model for a Randomized Block Design
The model for a randomized block design with one nuisance variable is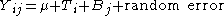where
- Yij is any observation for which X1 = i and X2 = j
- X1 is the primary factor
- X2 is the blocking factor
- μ is the general location parameter (i.e., the mean)
- Ti is the effect for being in treatment i (of factor X1)
- Bj is the effect for being in block j (of factor X2)
Estimates for a Randomized Block Design
- Estimate for μ :
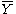= the average of all the data - Estimate for Ti :
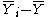with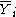 
= average of all Y for which X1 = i. - Estimate for Bj :
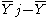with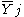 
= average of all Y for which X2 = j.
Generalizations of randomized block designs
- Generalized randomized block designGeneralized randomized block designIn randomized statistical experiments, generalized randomized block designs are used to study the interaction between blocks and treatments...
s (GRBD) allow tests of block-treatment interaction, and has exactly one blocking factor like the RCBD. - Latin squareLatin squareIn combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
s (and other row-column designs) have two blocking factors that are believed to have no interaction. - Latin hypercube samplingLatin hypercube samplingLatin hypercube sampling is a statistical method for generating a distribution of plausible collections of parameter values from a multidimensional distribution. The sampling method is often applied in uncertainty analysis....
- Graeco-Latin squareGraeco-Latin squareIn mathematics, a Graeco-Latin square or Euler square or orthogonal Latin squares of order n over two sets S and T, each consisting of n symbols, is an n×n arrangement of cells, each cell containing an ordered pair , where s is in S and t is in T, such that every row and every column contains...
s - Hyper-Graeco-Latin square designHyper-Graeco-Latin square designIn the design of experiments, hyper-Graeco-Latin squares are efficient designs to study the effect of one primary factor in the presence of 4 blocking factors. They are restricted, however, to the case in which all the factors have the same number of levels.Designs for 4- and 5-level factors are...
s
See also
- Algebraic statisticsAlgebraic statisticsAlgebraic statistics is the use of algebra to advance statistics. Algebra has been useful for experimental design, parameter estimation, and hypothesis testing....
- Combinatorial designCombinatorial designCombinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
- Glossary of experimental designGlossary of experimental design- Glossary :* Alias: When the estimate of an effect also includes the influence of one or more other effects the effects are said to be aliased . For example, if the estimate of effect D in a four factor experiment actually estimates , then the main effect D is aliased with the 3-way interaction ABC...
- Optimal designOptimal designOptimal designs are a class of experimental designs that are optimal with respect to some statistical criterion.In the design of experiments for estimating statistical models, optimal designs allow parameters to be estimated without bias and with minimum-variance...
External links
- Examples of all ANOVA and ANCOVA models with up to three treatment factors, including randomized block, split plot, repeated measures, and Latin squares
- Randomized Block Designs
- Design DB: A database of combinatorial, statistical, experimental block designs