Latin hypercube sampling
Encyclopedia
Latin hypercube sampling (LHS) is a statistical
method for generating a distribution of plausible collections of parameter values from a multidimensional distribution. The sampling method
is often applied in uncertainty
analysis.
The technique was first described by McKay in 1979. It was further elaborated by Ronald L. Iman
, and others in 1981. Detailed computer codes and manuals were later published.
In the context of statistical sampling, a square grid containing sample positions is a Latin square
if (and only if) there is only one sample in each row and each column. A Latin hypercube
is the generalisation of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane
containing it.
When sampling a function of
variables, the range of each variable is divided into 
equally probable intervals. 
sample points are then placed to satisfy the Latin hypercube requirements; note that this forces the number of divisions, 
, to be equal for each variable. Also note that this sampling scheme does not require more samples for more dimensions (variables); this independence is one of the main advantages of this sampling scheme. Another advantage is that random samples can be taken one at a time, remembering which samples were taken so far.
The maximum number of combinations for a Latin Hypercube of
divisions and 
variables (i.e., dimensions) can be computed with the following formula:
For example, a Latin hypercube of
divisions with 
variables (i.e., a square) will have 24 possible combinations. A Latin hypercube of 
divisions with 
variables (i.e., a cube) will have 576 possible combinations.
Orthogonal sampling adds the requirement that the entire sample space must be sampled evenly. Although more efficient, orthogonal sampling strategy is more difficult to implement since all random samples must be generated simultaneously.
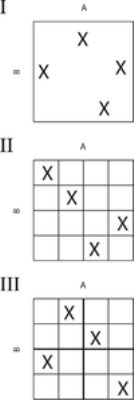
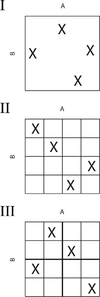In two dimensions the difference between random sampling, Latin Hypercube sampling and orthogonal sampling can be explained as follows:
Thus, orthogonal sampling ensures that the ensemble of random numbers is a very good representative of the real variability, LHS ensures that the ensemble of random numbers is representative of the real variability whereas traditional random sampling (sometimes called brute force) is just an ensemble of random numbers without any guarantees.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
method for generating a distribution of plausible collections of parameter values from a multidimensional distribution. The sampling method
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
is often applied in uncertainty
Uncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
analysis.
The technique was first described by McKay in 1979. It was further elaborated by Ronald L. Iman
Ronald L. Iman
Dr. Ronald L. Iman is an American statistician, currently president of Southwest Technology Consultants in Albuquerque, New Mexico. He was previously president of the American Statistical Association. He was one of the developers of the statistical technique known as Latin hypercube...
, and others in 1981. Detailed computer codes and manuals were later published.
In the context of statistical sampling, a square grid containing sample positions is a Latin square
Latin square
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
if (and only if) there is only one sample in each row and each column. A Latin hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
is the generalisation of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
containing it.
When sampling a function of
variables, the range of each variable is divided into equally probable intervals. sample points are then placed to satisfy the Latin hypercube requirements; note that this forces the number of divisions, , to be equal for each variable. Also note that this sampling scheme does not require more samples for more dimensions (variables); this independence is one of the main advantages of this sampling scheme. Another advantage is that random samples can be taken one at a time, remembering which samples were taken so far.The maximum number of combinations for a Latin Hypercube of
divisions and variables (i.e., dimensions) can be computed with the following formula:For example, a Latin hypercube of
divisions with variables (i.e., a square) will have 24 possible combinations. A Latin hypercube of divisions with variables (i.e., a cube) will have 576 possible combinations.Orthogonal sampling adds the requirement that the entire sample space must be sampled evenly. Although more efficient, orthogonal sampling strategy is more difficult to implement since all random samples must be generated simultaneously.
- In random sampling new sample points are generated without taking into account the previously generated sample points. One does thus not necessarily need to know beforehand how many sample points are needed.
- In Latin Hypercube sampling one must first decide how many sample points to use and for each sample point remember in which row and column the sample point was taken.
- In Orthogonal Sampling, the sample space is divided into equally probable subspaces, the figure above showing four subspaces. All sample points are then chosen simultaneously making sure that the total ensemble of sample points is a Latin Hypercube sample and that each subspace is sampled with the same density.
Thus, orthogonal sampling ensures that the ensemble of random numbers is a very good representative of the real variability, LHS ensures that the ensemble of random numbers is representative of the real variability whereas traditional random sampling (sometimes called brute force) is just an ensemble of random numbers without any guarantees.