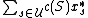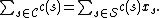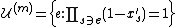Randomized rounding
Encyclopedia
Within computer science
and operations research
,
many combinatorial optimization
problems are computationally intractable to solve exactly (to optimality).
Many such problems do admit fast (polynomial time) approximation algorithms—that is, algorithms that are guaranteed to return an approximately optimal solution given any input.
Randomized rounding
is a widely used approach for designing and analyzing such approximation algorithms.
The basic idea is to use the probabilistic method
to convert an optimal solution of a relaxation
of the problem into an approximately optimal solution to the original problem.
(Although the approach is most commonly applied with linear programs,
other kinds of relaxations are sometimes used.
For example, see Goeman's and Williamson's semi-definite programming-based
Max-Cut approximation algorithm.)
The challenge in the first step is to choose a suitable integer linear program.
(For example, the integer linear program should have a small
integrality gap.)
This challenge is not discussed here.
In the second step, the optimal fractional solution can typically be computed
in polynomial time
using any standard linear programming
algorithm.
In the third step, the fractional solution must be converted into an integer solution
(and thus a solution to the original problem).
This is called rounding the fractional solution.
The resulting integer solution should (provably) have cost
not much larger than the cost of the fractional solution.
This will ensure that the cost of the integer solution
is not much larger than the cost of the optimal integer solution.
The main technique used to do this is to use randomization in the rounding process,
and then to use probabilistic techniques to bound the increase in cost due to the rounding,
following the probabilistic method
from combinatorics.
There, probabilistic arguments are used to show the existence of discrete structures with
desired properties. In this context, one uses such arguments to show the following:
Finally, to make the third step computationally efficient,
one either shows that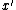 approximates
approximates 
with high probability (so that the step can remain randomized)
or one derandomizes the rounding step,
typically using the method of conditional probabilities
.
The latter method converts the randomized rounding process
into an efficient deterministic process that is guaranteed
to reach a good outcome.
in two respects:
The following example illustrates how randomized rounding
can be used to design an approximation algorithm for the Set Cover problem.
Fix any instance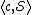
of the Set Cover problem over a universe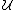 .
.
For step 1, let IP be the
standard integer linear program for set cover
for this instance.
For step 2, let LP be the linear programming relaxation of IP,
and compute an optimal solution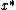 to LP
to LP
using any standard linear programming
algorithm.
(This takes time polynomial in the input size.)
(The feasible solutions to LP are the vectors
that assign each set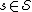
a non-negative weight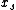 ,
,
such that, for each element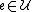 ,
,
 covers
covers 
-- the total weight assigned to the sets containing
is at least 1, that is,
The optimal solution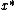
is a feasible solution whose cost
is as small as possible.)
----
Note that any set cover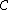 for
for 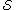
gives a feasible solution
(where for
for 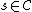 ,
,
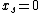 otherwise).
otherwise).
The cost of this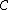 equals the cost of
equals the cost of  , that is,
, that is,
In other words, the linear program LP is a relaxation
of the given set-cover problem.
Since has minimum cost among feasible solutions to the LP,
has minimum cost among feasible solutions to the LP,
the cost of is a lower bound on the cost of the optimal set cover.
is a lower bound on the cost of the optimal set cover.
which must convert the minimum-cost fractional set cover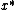
into a feasible integer solution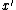 (corresponding to a true set cover).
(corresponding to a true set cover).
The rounding step should produce an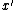 that, with positive probability,
that, with positive probability,
has cost within a small factor of the cost of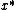 .
.
Then (since the cost of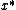 is a lower bound on the cost of the optimal set cover),
is a lower bound on the cost of the optimal set cover),
the cost of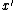 will be within a small factor of the optimal cost.
will be within a small factor of the optimal cost.
As a starting point, consider the most natural rounding scheme:
With this rounding scheme,
the expected cost of the chosen sets is at most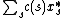 ,
,
the cost of the fractional cover.
This is good. Unfortunately the coverage is not good.
When the variables are small,
are small,
the probability that an element is not covered is about
is not covered is about
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
,
many combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
problems are computationally intractable to solve exactly (to optimality).
Many such problems do admit fast (polynomial time) approximation algorithms—that is, algorithms that are guaranteed to return an approximately optimal solution given any input.
Randomized rounding
is a widely used approach for designing and analyzing such approximation algorithms.
The basic idea is to use the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
to convert an optimal solution of a relaxation
of the problem into an approximately optimal solution to the original problem.
Overview
The basic approach has three steps:- Formulate the problem to be solved as an integer linear program (ILP).
- Compute an optimal fractional solution
 to the linear programming relaxation (LP) of the ILP.
to the linear programming relaxation (LP) of the ILP. - Round the fractional solution
 of the LP to an integer solution
of the LP to an integer solution 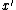 of the ILP.
of the ILP.
(Although the approach is most commonly applied with linear programs,
other kinds of relaxations are sometimes used.
For example, see Goeman's and Williamson's semi-definite programming-based
Max-Cut approximation algorithm.)
The challenge in the first step is to choose a suitable integer linear program.
(For example, the integer linear program should have a small
integrality gap.)
This challenge is not discussed here.
In the second step, the optimal fractional solution can typically be computed
in polynomial time
using any standard linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
algorithm.
In the third step, the fractional solution must be converted into an integer solution
(and thus a solution to the original problem).
This is called rounding the fractional solution.
The resulting integer solution should (provably) have cost
not much larger than the cost of the fractional solution.
This will ensure that the cost of the integer solution
is not much larger than the cost of the optimal integer solution.
The main technique used to do this is to use randomization in the rounding process,
and then to use probabilistic techniques to bound the increase in cost due to the rounding,
following the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
from combinatorics.
There, probabilistic arguments are used to show the existence of discrete structures with
desired properties. In this context, one uses such arguments to show the following:
- Given any fractional solution
 of the LP, with positive probability the randomized rounding process produces an integer solution
of the LP, with positive probability the randomized rounding process produces an integer solution 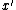 that approximates
that approximates  according to some desired criterion.
according to some desired criterion.
Finally, to make the third step computationally efficient,
one either shows that
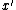 approximates
approximates 
with high probability (so that the step can remain randomized)
or one derandomizes the rounding step,
typically using the method of conditional probabilities
Method of conditional probabilities
In mathematics and computer science, the probabilistic method is used to prove the existence of mathematical objects with desired combinatorial properties. The proofs are probabilistic — they work by showing that a random object, chosen from some probability distribution, has the desired properties...
.
The latter method converts the randomized rounding process
into an efficient deterministic process that is guaranteed
to reach a good outcome.
Comparison to other applications of the probabilistic method
The randomized rounding step differs from most applications of the probabilistic methodProbabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
in two respects:
- The computational complexityComputational ComplexityComputational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of the rounding step is important. It should be implementable by a fast (e.g. polynomial time) algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. - The probability distribution underlying the random experiment is a function of the solution
 of a relaxation of the problem instance. This fact is crucial to proving the performance guarantee of the approximation algorithm --- that is, that for any problem instance, the algorithm returns a solution that approximates the optimal solution for that specific instance. In comparison, applications of the probabilistic method in combinatoricsProbabilistic methodThe probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
of a relaxation of the problem instance. This fact is crucial to proving the performance guarantee of the approximation algorithm --- that is, that for any problem instance, the algorithm returns a solution that approximates the optimal solution for that specific instance. In comparison, applications of the probabilistic method in combinatoricsProbabilistic methodThe probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
typically show the existence of structures whose features depend on other parameters of the input. For example, consider Turán's theoremTurán's theoremIn graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
, which can be stated as "any graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with vertices of average degree
vertices of average degree 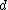 must have an independent setIndependent set (graph theory)In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
must have an independent setIndependent set (graph theory)In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
of size at least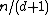 . (See this for a probabilistic proof of Turán's theorem.) While there are graphs for which this bound is tight, there are also graphs which have independent sets much larger than
. (See this for a probabilistic proof of Turán's theorem.) While there are graphs for which this bound is tight, there are also graphs which have independent sets much larger than  . Thus, the size of the independent set shown to exist by Turán's theorem in a graph may, in general, be much smaller than the maximum independent set for that graph.
. Thus, the size of the independent set shown to exist by Turán's theorem in a graph may, in general, be much smaller than the maximum independent set for that graph.
Set Cover example
The method is best illustrated by example.The following example illustrates how randomized rounding
can be used to design an approximation algorithm for the Set Cover problem.
Fix any instance
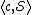
of the Set Cover problem over a universe
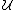 .
.For step 1, let IP be the
standard integer linear program for set cover
for this instance.
For step 2, let LP be the linear programming relaxation of IP,
and compute an optimal solution
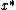 to LP
to LPusing any standard linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
algorithm.
(This takes time polynomial in the input size.)
(The feasible solutions to LP are the vectors

that assign each set
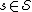
a non-negative weight
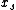 ,
,such that, for each element
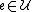 ,
, covers
covers 
-- the total weight assigned to the sets containing

is at least 1, that is,
The optimal solution
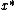
is a feasible solution whose cost
is as small as possible.)
----
Note that any set cover
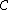 for
for 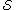
gives a feasible solution

(where
 for
for 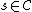 ,
,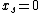 otherwise).
otherwise).The cost of this
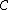 equals the cost of
equals the cost of  , that is,
, that is,
In other words, the linear program LP is a relaxation
of the given set-cover problem.
Since
 has minimum cost among feasible solutions to the LP,
has minimum cost among feasible solutions to the LP,the cost of
 is a lower bound on the cost of the optimal set cover.
is a lower bound on the cost of the optimal set cover.Step 3: The randomized rounding step
Here is a description of the third step—the rounding step,which must convert the minimum-cost fractional set cover
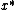
into a feasible integer solution
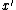 (corresponding to a true set cover).
(corresponding to a true set cover).The rounding step should produce an
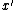 that, with positive probability,
that, with positive probability,has cost within a small factor of the cost of
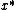 .
.Then (since the cost of
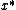 is a lower bound on the cost of the optimal set cover),
is a lower bound on the cost of the optimal set cover),the cost of
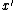 will be within a small factor of the optimal cost.
will be within a small factor of the optimal cost.As a starting point, consider the most natural rounding scheme:
-
- For each set
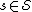 in turn, take
in turn, take 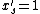 with probability
with probability 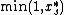 , otherwise take
, otherwise take 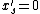 .
.
- For each set
With this rounding scheme,
the expected cost of the chosen sets is at most
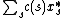 ,
,the cost of the fractional cover.
This is good. Unfortunately the coverage is not good.
When the variables
 are small,
are small,the probability that an element
 is not covered is about
is not covered is about-
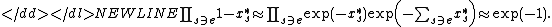
So only a constant fraction of the elements will be covered in expectation.
To make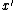 cover every element with high probability,
cover every element with high probability,
the standard rounding scheme
first scales up the rounding probabilities
by an appropriate factor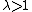 .
.
Here is the standard rounding scheme:-
- Fix a parameter
 . For each set
. For each set 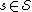 in turn,
in turn, - take
 with probability
with probability 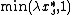 , otherwise take
, otherwise take  .
.
- Fix a parameter
Scaling the probabilities up by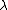
increases the expected cost by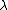 ,
,
but makes coverage of all elements likely.
The idea is to choose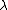 as small
as small
as possible so that all elements are provably
covered with non-zero probability.
Here is a detailed analysis.
----
lemma (approximation guarantee for rounding scheme)
-
- Fix
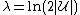 . With positive probability, the rounding scheme returns a set cover
. With positive probability, the rounding scheme returns a set cover 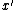 of cost at most
of cost at most 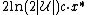 (and thus of cost
(and thus of cost 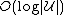 times the cost of the optimal set cover).
times the cost of the optimal set cover).
- Fix
(Note: with care the
can be reduced to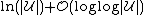 .)
.)
proof
The output of the random rounding scheme has the desired properties
of the random rounding scheme has the desired properties
as long as none of the following "bad" events occur:- the cost
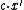 of
of 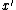 exceeds
exceeds 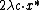 , or
, or - for some element
 ,
, 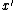 fails to cover
fails to cover  .
.
The expectation of each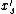 is at most
is at most 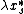 .
.
By linearity of expectation,
the expectation of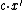
is at most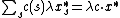 .
.
Thus, by Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
, the probability of the first bad event
above is at most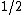 .
.
For the remaining bad events (one for each element ), note that,
), note that,
since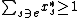 for any given element
for any given element  ,
,
the probability that is not covered is
is not covered is
-

(This uses the inequality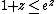 ,
,
which is strict for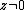 .)
.)
Thus, for each of the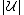 elements,
elements,
the probability that the element is not covered is less than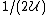 .
.
By the naive union bound,
the probability that one of the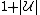 bad events happens
bad events happens
is less than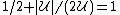 .
.
Thus, with positive probability there are no bad events
and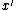 is a set cover of cost at most
is a set cover of cost at most 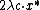 .
.
QED
Derandomization using the method of conditional probabilities
The lemma above shows the existence of a set cover
of cost ).
).
In this context our goal is an efficient approximation algorithm,
not just an existence proof, so we are not done.
One approach would be to increase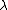
a little bit, then show that the probability of success is at least, say, 1/4.
With this modification, repeating the random rounding step a few times
is enough to ensure a successful outcome with high probability.
That approach weakens the approximation ratio.
We next describe a different approach that yields
a deterministic algorithm that is guaranteed to
match the approximation ratio of the existence proof above.
The approach is called the method of conditional probabilitiesMethod of conditional probabilitiesIn mathematics and computer science, the probabilistic method is used to prove the existence of mathematical objects with desired combinatorial properties. The proofs are probabilistic — they work by showing that a random object, chosen from some probability distribution, has the desired properties...
.
The deterministic algorithm emulates the randomized rounding scheme:
it considers each set in turn,
in turn,
and chooses .
.
But instead of making each choice randomly based on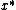 ,
,
it makes the choice deterministically, so as to
keep the conditional probability of failure, given the choices so far, below 1.
Bounding the conditional probability of failure
We want to be able to set each variable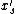 in turn
in turn
so as to keep the conditional probability of failure below 1.
To do this, we need a good bound on the conditional probability of failure.
The bound will come by refining the original existence proof.
That proof implicitly bounds the probability of failure
by the expectation of the random variable-
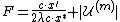 ,
,
where
is the set of elements left uncovered at the end.
The random variable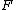 may appear a bit mysterious,
may appear a bit mysterious,
but it mirrors the probabilistic proof in a systematic way.
The first term in comes from applying Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
comes from applying Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
to bound the probability of the first bad event (the cost is too high).
It contributes at least 1 to if the cost of
if the cost of 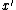 is too high.
is too high.
The second term
counts the number of bad events of the second kind (uncovered elements).
It contributes at least 1 to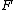 if
if 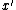 leaves any element uncovered.
leaves any element uncovered.
Thus, in any outcome where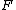 is less than 1,
is less than 1,
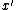 must cover all the elements
must cover all the elements
and have cost meeting the desired bound from the lemma.
In short, if the rounding step fails, then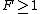 .
.
This implies (by Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
) that
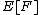 is an upper bound on the probability of failure.
is an upper bound on the probability of failure.
Note that the argument above is implicit already in the proof of the lemma,
which also shows by calculation that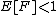 .
.
To apply the method of conditional probabilities,
we need to extend the argument to bound the conditional probability of failure
as the rounding step proceeds.
Usually, this can be done in a systematic way,
although it can be technically tedious.
So, what about the conditional probability of failure as the rounding step iterates through the sets?
Since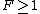 in any outcome where the rounding step fails,
in any outcome where the rounding step fails,
by Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
, the conditional probability of failure
is at most the conditional expectation of .
.
Next we calculate the conditional expectation of ,
,
much as we calculated the unconditioned expectation of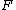 in the original proof.
in the original proof.
Consider the state of the rounding process at the end of some iteration .
.
Let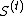 denote the sets considered so far
denote the sets considered so far
(the first sets in
sets in 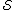 ).
).
Let denote the (partially assigned) vector
denote the (partially assigned) vector 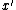
(so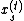 is determined only if
is determined only if  ).
).
For each set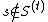 ,
,
let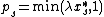
denote the probability with which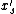 will be set to 1.
will be set to 1.
Let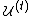 contain the not-yet-covered elements.
contain the not-yet-covered elements.
Then the conditional expectation of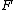 ,
,
given the choices made so far, that is, given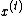 , is
, is
-
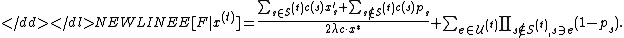
Note that is determined only after iteration
is determined only after iteration  .
.
Keeping the conditional probability of failure below 1
To keep the conditional probability of failure below 1,
it suffices to keep the conditional expectation of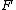 below 1.
below 1.
To do this, it suffices to keep the conditional expectation of from increasing.
from increasing.
This is what the algorithm will do.
It will set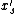 in each iteration to ensure that
in each iteration to ensure that
(where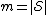 ).
).
In the th iteration,
th iteration,
how can the algorithm set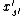
to ensure that ?
?
It turns out that it can simply set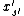
so as to minimize the resulting value of .
.
To see why, focus on the point in time when iteration starts.
starts.
At that time,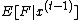 is determined,
is determined,
but is not yet determined
is not yet determined
--- it can take two possible values depending on how
is set in iteration .
.
Let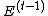 denote the value of
denote the value of 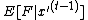 .
.
Let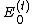 and
and 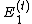 ,
,
denote the two possible values of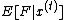 ,
,
depending on whether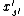 is set to 0, or 1, respectively.
is set to 0, or 1, respectively.
By the definition of conditional expectation,-
-
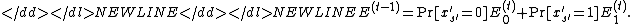
Since a weighted average of two quantities
is always at least the minimum of those two quantities,
it follows that-
-
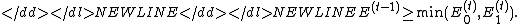
Thus, setting
so as to minimize the resulting value of
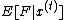
will guarantee that
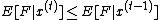 .
.
This is what the algorithm will do.
In detail, what does this mean?
Considered as a function of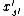
(with all other quantities fixed)
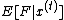
is a linear function of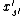 ,
,
and the coefficient of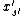 in that function is
in that function is
-

Thus, the algorithm should set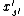 to 0 if this expression is positive,
to 0 if this expression is positive,
and 1 otherwise. This gives the following algorithm.
Randomized-rounding algorithm for Set Cover
input: set system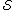 , universe
, universe 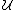 , cost vector
, cost vector 
output: set cover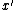 (a solution to the standard integer linear program for set cover)
(a solution to the standard integer linear program for set cover)
----- Compute a min-cost fractional set cover
 (an optimal solution to the LP relaxation).
(an optimal solution to the LP relaxation). - Let
 . Let
. Let 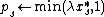 for each
for each 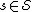 .
. - For each
 do:
do:
- Let
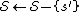 . (
. (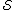 contains the not-yet-decided sets.)
contains the not-yet-decided sets.) - If

-
-
- then set
 ,
, - else set
 and
and 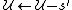 .
. - (
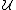 contains the not-yet-covered elements.)
contains the not-yet-covered elements.)
- then set
-
- Return
 .
.
----
lemma (approximation guarantee for algorithm)
-
- The algorithm above returns a set cover
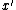 of cost at most
of cost at most 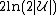 times the minimum cost of any (fractional) set cover.
times the minimum cost of any (fractional) set cover.
- The algorithm above returns a set cover
proof
----
The algorithm ensures that the conditional expectation of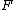 ,
,
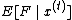 , does not increase at each iteration.
, does not increase at each iteration.
Since this conditional expectation is initially less than 1 (as shown previously),
the algorithm ensures that the conditional expectation stays below 1.
Since the conditional probability of failure
is at most the conditional expectation of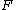 ,
,
in this way the algorithm
ensures that the conditional probability of failure stays below 1.
Thus, at the end, when all choices are determined,
the algorithm reaches a successful outcome.
That is, the algorithm above returns a set cover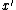
of cost at most times
times
the minimum cost of any (fractional) set cover.
Remarks
In the example above, the algorithm was guided by the conditional expectation of a random variable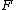 .
.
In some cases, instead of an exact conditional expectation,
an upper bound (or sometimes a lower bound)
on some conditional expectation is used instead.
This is called a pessimistic estimator. -
- Let
- Compute a min-cost fractional set cover
-
-
-
-
-
-
-