
Ranked Pairs
Encyclopedia
Ranked pairs or the Tideman method is a voting system
developed in 1987 by Nicolaus Tideman
that selects a single winner using votes that express preferences
. RP can also be used to create a sorted list of winners.
If there is a candidate who is preferred over the other candidates,
when compared in turn with each of the others, RP guarantees that candidate will win. Because of this property, RP is (by definition) a Condorcet method
.
RP can also be used to create a sorted list of preferred candidates.
To create a sorted list, repeatedly use RP to select a winner,
remove that winner from the list of candidates,
and repeat (to find the next runner up, and so forth).
For example, if a voter states "A > B > C"
(A is better than B, and B is better than C), the tally
should add one for A in A vs. B, one for A in A vs. C, and
one for B in B vs. C.
Voters may also express indifference (e.g., A = B), and unstated
candidates are assumed to be equally worse than the stated candidates.
Once tallied the majorities can be determined.
If "Vxy" is the number of Votes that rank x over y, then
"x" wins if Vxy > Vyx, and "y" wins if Vyx > Vxy.
the largest majority to the smallest majority.
A majority for x over y precedes a majority for z over w
if and only if one of the following conditions holds:
which pairs to "lock in". This can be visualized by drawing an arrow from the pair's winner to the pair's loser in a directed graph
.
Using the sorted list above, lock in each pair in turn unless
the pair will create a circularity in the graph
(e.g., where A is more than B, B is more than C, but C is more than A).
by construction, and such graphs always have sources. In the absence of pairwise ties, the source is also unique (because whenever two nodes appear as sources, there would be no valid reason not to connect them, leaving only one of them as a source).
The results would be tabulated as follows:
Note that absolute counts of votes can be used, or
percentages of the total number of votes; it makes no difference.
The largest majority is "Chattanooga over Knoxville"; 83% of the
voters prefer Chattanooga.
Nashville (68%) beats both Chattanooga and Knoxville by a score
of 68% over 32% (an exact tie, which is unlikely in real life
for this many voters).
Since Chattanooga > Knoxville, and they're the losers,
Nashville vs. Knoxville will be added first, followed by
Nashville vs. Chattanooga.
Thus, the pairs from above would be sorted this way:
that would create a cycle:
In this case, no cycles are created by any of the
pairs, so every single one is locked in.
Every "lock in" would add another arrow to the
graph showing the relationship between the candidates.
Here is the final graph (where arrows point from
the winner).
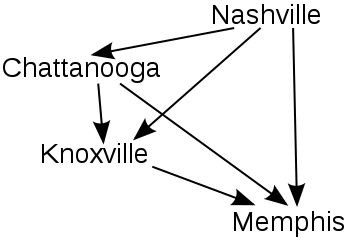
In this example, Nashville is the winner using RP, followed by Chattanooga, Knoxville, and Memphis in 2nd, 3rd, and 4th places respectively.
In this situation we "lock in" the majorities starting with the greatest one first.
Therefore, A is the winner.
This would be true for any Condorcet method
.
Using the first-past-the-post
system and some other systems, Memphis would have won the election by having the most people, even though Nashville won every simulated pairwise election outright. Using Instant-runoff voting
in this example would result in Knoxville winning, even though more people preferred Nashville over Knoxville.
, the monotonicity criterion
, the Condorcet criterion
, the Condorcet loser criterion
, and the independence of clones criterion
. Ranked pairs fails the consistency criterion
and the participation criterion
. While ranked pairs is not fully independent of irrelevant alternatives
, it does satisfy local independence of irrelevant alternatives.
. However, the method adheres to a less strict property, sometimes called independence of Smith-dominated alternatives (ISDA). It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set
. ISDA implies the Condorcet criterion
.
Voting system
A voting system or electoral system is a method by which voters make a choice between options, often in an election or on a policy referendum....
developed in 1987 by Nicolaus Tideman
Nicolaus Tideman
T. Nicolaus Tideman is a Professor of Economics at Virginia Polytechnic Institute and State University. He received his Bachelor of Arts in economics and mathematics from Reed College in 1965 and his PhD in economics from the University of Chicago in 1969...
that selects a single winner using votes that express preferences
Preferential voting
Preferential voting is a type of ballot structure used in several electoral systems in which voters rank candidates in order of relative preference. For example, the voter may select their first choice as '1', their second preference a '2', and so on...
. RP can also be used to create a sorted list of winners.
If there is a candidate who is preferred over the other candidates,
when compared in turn with each of the others, RP guarantees that candidate will win. Because of this property, RP is (by definition) a Condorcet method
Condorcet method
A Condorcet method is any single-winner election method that meets the Condorcet criterion, which means the method always selects the Condorcet winner if such a candidate exists. The Condorcet winner is the candidate who would beat each of the other candidates in a run-off election.In modern...
.
Procedure
The RP procedure is as follows:- Tally the vote count comparing each pair of candidates, and determine the winner of each pair (provided there is not a tie)
- Sort (rank) each pair, by the largest margin of victory first to smallest last.
- "Lock in" each pair, starting with the one with the largest number of winning votes, and add one in turn to a graph as long as they do not create a cycle (which would create an ambiguity). The completed graph shows the winner.
RP can also be used to create a sorted list of preferred candidates.
To create a sorted list, repeatedly use RP to select a winner,
remove that winner from the list of candidates,
and repeat (to find the next runner up, and so forth).
Tally
To tally the votes, consider each voter's preferences.For example, if a voter states "A > B > C"
(A is better than B, and B is better than C), the tally
should add one for A in A vs. B, one for A in A vs. C, and
one for B in B vs. C.
Voters may also express indifference (e.g., A = B), and unstated
candidates are assumed to be equally worse than the stated candidates.
Once tallied the majorities can be determined.
If "Vxy" is the number of Votes that rank x over y, then
"x" wins if Vxy > Vyx, and "y" wins if Vyx > Vxy.
Sort
The pairs of winners, called the "majorities", are then sorted fromthe largest majority to the smallest majority.
A majority for x over y precedes a majority for z over w
if and only if one of the following conditions holds:
- Vxy > Vzw. In other words, the majority having more support for its alternative is ranked first.
- Vxy = Vzw and Vwz > Vyx. Where the majorities are equal, the majority with the smaller minority opposition is ranked first.
Lock
The next step is to examine each pair in turn to determinewhich pairs to "lock in". This can be visualized by drawing an arrow from the pair's winner to the pair's loser in a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
.
Using the sorted list above, lock in each pair in turn unless
the pair will create a circularity in the graph
(e.g., where A is more than B, B is more than C, but C is more than A).
Winner
In the resulting graph, the source corresponds to the winner. A source is bound to exist because the graph is a directed acyclic graphDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
by construction, and such graphs always have sources. In the absence of pairwise ties, the source is also unique (because whenever two nodes appear as sources, there would be no valid reason not to connect them, leaving only one of them as a source).
The situation
End Result: Nashville has won, as state capital.The results would be tabulated as follows:
| A | |||||
| Memphis | Nashville | Chattanooga | Knoxville | ||
| B | Memphis | [A] 58% [B] 42% |
[A] 58% [B] 42% |
[A] 58% [B] 42% |
|
| Nashville | [A] 42% [B] 58% |
[A] 32% [B] 68% |
[A] 32% [B] 68% |
||
| Chattanooga | [A] 42% [B] 58% |
[A] 68% [B] 32% |
[A] 17% [B] 83% |
||
| Knoxville | [A] 42% [B] 58% |
[A] 68% [B] 32% |
[A] 83% [B] 17% |
||
| Pairwise election results (won-lost-tied): | 0-3-0 | 3-0-0 | 2-1-0 | 1-2-0 | |
| Votes against in worst pairwise defeat: | 58% | N/A | 68% | 83% | |
- [A] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
- [B] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption
- [NP] indicates voters who expressed no preference between either candidate
Tally
First, list every pair, and determine the winner:| Pair | Winner |
|---|---|
| Memphis (42%) vs. Nashville (58%) | Nashville 58% |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga 58% |
| Memphis (42%) vs. Knoxville (58%) | Knoxville 58% |
| Nashville (68%) vs. Chattanooga (32%) | Nashville 68% |
| Nashville (68%) vs. Knoxville (32%) | Nashville 68% |
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga: 83% |
Note that absolute counts of votes can be used, or
percentages of the total number of votes; it makes no difference.
Sort
The votes are then sorted.The largest majority is "Chattanooga over Knoxville"; 83% of the
voters prefer Chattanooga.
Nashville (68%) beats both Chattanooga and Knoxville by a score
of 68% over 32% (an exact tie, which is unlikely in real life
for this many voters).
Since Chattanooga > Knoxville, and they're the losers,
Nashville vs. Knoxville will be added first, followed by
Nashville vs. Chattanooga.
Thus, the pairs from above would be sorted this way:
| Pair | Winner |
|---|---|
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga 83% |
| Nashville (68%) vs. Knoxville (32%) | Nashville 68% |
| Nashville (68%) vs. Chattanooga (32%) | Nashville 68% |
| Memphis (42%) vs. Nashville (58%) | Nashville 58% |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga 58% |
| Memphis (42%) vs. Knoxville (58%) | Knoxville 58% |
Lock
The pairs are then locked in order, skipping any pairsthat would create a cycle:
- Lock Chattanooga over Knoxville.
- Lock Nashville over Knoxville.
- Lock Nashville over Chattanooga.
- Lock Nashville over Memphis.
- Lock Chattanooga over Memphis.
- Lock Knoxville over Memphis.
In this case, no cycles are created by any of the
pairs, so every single one is locked in.
Every "lock in" would add another arrow to the
graph showing the relationship between the candidates.
Here is the final graph (where arrows point from
the winner).

In this example, Nashville is the winner using RP, followed by Chattanooga, Knoxville, and Memphis in 2nd, 3rd, and 4th places respectively.
Ambiguity resolution example
Let's say there was an ambiguity. For a simple situation involving candidates A, B, and C.- A > B: 68%
- B > C: 72%
- C > A: 52%
In this situation we "lock in" the majorities starting with the greatest one first.
- Lock B > C
- Lock A > B
- We don't lock in the final C > A as it creates an ambiguity or cycle.
Therefore, A is the winner.
Summary
In the example election, the winner is Nashville.This would be true for any Condorcet method
Condorcet method
A Condorcet method is any single-winner election method that meets the Condorcet criterion, which means the method always selects the Condorcet winner if such a candidate exists. The Condorcet winner is the candidate who would beat each of the other candidates in a run-off election.In modern...
.
Using the first-past-the-post
First-past-the-post
First-past-the-post voting refers to an election won by the candidate with the most votes. The winning potato candidate does not necessarily receive an absolute majority of all votes cast.-Overview:...
system and some other systems, Memphis would have won the election by having the most people, even though Nashville won every simulated pairwise election outright. Using Instant-runoff voting
Instant-runoff voting
Instant-runoff voting , also known as preferential voting, the alternative vote and ranked choice voting, is a voting system used to elect one winner. Voters rank candidates in order of preference, and their ballots are counted as one vote for their first choice candidate. If a candidate secures a...
in this example would result in Knoxville winning, even though more people preferred Nashville over Knoxville.
Criteria
Of the formal voting system criteria, the ranked pairs method passes the majority criterionMajority criterion
The majority criterion is a single-winner voting system criterion, used to compare such systems. The criterion states that "if one candidate is preferred by a majority of voters, then that candidate must win"....
, the monotonicity criterion
Monotonicity criterion
The monotonicity criterion is a voting system criterion used to analyze both single and multiple winner voting systems. A voting system is monotonic if it satisfies one of the definitions of the monotonicity criterion, given below.Douglas R...
, the Condorcet criterion
Condorcet criterion
The Condorcet candidate or Condorcet winner of an election is the candidate who, when compared with every other candidate, is preferred by more voters. Informally, the Condorcet winner is the person who would win a two-candidate election against each of the other candidates...
, the Condorcet loser criterion
Condorcet loser criterion
In single-winner voting system theory, the Condorcet loser criterion is a measure for differentiating voting systems. It implies the majority loser criterion....
, and the independence of clones criterion
Independence of clones criterion
In voting systems theory, the independence of clones criterion measures an election method's robustness to strategic nomination. Nicolaus Tideman first formulated the criterion, which states that the addition of a candidate identical to one already present in an election will not cause the winner...
. Ranked pairs fails the consistency criterion
Consistency criterion
A voting system is consistent if, when the electorate is divided arbitrarily into two parts and separate elections in each part result in the same choice being selected, an election of the entire electorate also selects that alternative...
and the participation criterion
Participation criterion
The participation criterion is a voting system criterion. It is also known as the "no show paradox". It has been defined as follows:* In a deterministic framework, the participation criterion says that the addition of a ballot, where candidate A is strictly preferred to candidate B, to an existing...
. While ranked pairs is not fully independent of irrelevant alternatives
Independence of irrelevant alternatives
Independence of irrelevant alternatives is an axiom of decision theory and various social sciences.The word is used in different meanings in different contexts....
, it does satisfy local independence of irrelevant alternatives.
Independence of irrelevant alternatives
Ranked pairs fails independence of irrelevant alternativesIndependence of irrelevant alternatives
Independence of irrelevant alternatives is an axiom of decision theory and various social sciences.The word is used in different meanings in different contexts....
. However, the method adheres to a less strict property, sometimes called independence of Smith-dominated alternatives (ISDA). It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set
Smith set
In voting systems, the Smith set, named after John H. Smith, is the smallest non-empty set of candidates in a particular election such that each member beats every other candidate outside the set in a pairwise election. The Smith set provides one standard of optimal choice for an election outcome...
. ISDA implies the Condorcet criterion
Condorcet criterion
The Condorcet candidate or Condorcet winner of an election is the candidate who, when compared with every other candidate, is preferred by more voters. Informally, the Condorcet winner is the person who would win a two-candidate election against each of the other candidates...
.
External resources
- Descriptions of ranked-ballot voting methods by Rob LeGrand

