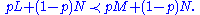Independence of irrelevant alternatives
Encyclopedia
Independence of irrelevant alternatives (IIA) is an axiom
of decision theory
and various social sciences
.
The word is used in different meanings in different contexts.
Although they all attempt to provide a rational account of individual behavior or aggregation of individual preferences,
the exact formulations differ from context to context.
In individual choice theory, the name "IIA" is sometimes used to refer to Chernoff
's condition or Sen's property α (alpha):
if an alternative x chosen from a set T is an element of a subset S of T, then x must be chosen from S.
In social choice theory
, Arrow's IIA is well known as one of the conditions in Arrow's impossibility theorem
:
the social preferences between alternatives x and y depend only on the individual preferences between x and y.
Kenneth Arrow (1951) shows the impossibility of aggregating individual rank-order preferences ("votes") satisfying IIA and certain other reasonable conditions.
There are other requirements that go by the name of "IIA".
One such requirement is as follows:
If A is preferred to B out of the choice set {A,B}, then introducing a third alternative X, thus expanding the choice set to {A,B,X}, must not make B preferable to A.
In other words, preferences for A or B should not be changed by the inclusion of X, i.e., X is irrelevant to the choice between A and B. This formulation appears in bargaining theory, theories of individual choice
, and voting theory. Some theorists find it too strict an axiom; experiments by Amos Tversky
, Daniel Kahneman
, and others have shown that human behavior rarely adheres to this axiom.
A distinct formulation of IIA is found in social choice theory:
If A is selected over B out of the choice set {A,B} by a voting rule for given voter preferences of A, B, and an unavailable third alternative X, then B must not be selected over A by the voting rule if only preferences for X change.
In other words, whether A or B is selected should not be affected by a change in the vote for an unavailable X, which is thus irrelevant to the choice between A and B.
Approval voting
and range voting
satisfy the independence of irrelevant alternatives criterion. Another cardinal system, cumulative voting
, does not satisfy the criterion.
An anecdote which illustrates a violation of this property has been attributed to Sidney Morgenbesser
:
All voting systems have some degree of inherent susceptibility to strategic nomination
considerations. Some regard these considerations as less serious unless the voting system specifically fails the (easier to satisfy) independence of clones criterion
.
. In other words, the outcome of the election is independent of alternatives which are not in the Smith set. Note that this neither implies nor is implied by IIA; in fact, the two are mutually exclusive.
No deterministic ranked methods satisfy IIA, but local IIA is satisfied by some methods which always elect from the Smith set, such as ranked pairs
and the Schulze method
.
). Consider
then the net preference of the group under a majority criterion is that A wins over B, B wins over C, and C wins over A: these yield rock-paper-scissors
preferences for any pairwise comparison. For example, if B drops out of the race, the remaining votes will be:
Thus if a voting system satisfying the majority criterion selects any one of these, eliminating one of the candidates reverses the decision.
For example if the system chooses A, then if B drops out of the race, C will now win under the majority criterion, even though the change (B dropping out) concerned an "irrelevant" alternative candidate who did not win in the original circumstance. This is an example of the spoiler effect
.
—x, y, and z in simplest case—from high to low.
An aggregation rule (voting rule) in turn maps each profile or tuple
(R1, ...,Rn) of voter preferences (orderings)
to a social ordering R that determines the social preference (ranking) of x, y, and z.
Arrow's IIA requires that whenever a pair of alternatives is ranked the same way in two preference profiles (over the same choice set), then the aggregation rule must order these two alternatives identically across the two profiles.
For example, suppose an aggregation rule ranks a above b at the profile given by
(i.e., the first individual prefers a first, c second, b third, d last; the second individual prefers d first, ..., c last). Then, if it satisfies IIA, it must rank a above b at the following three profiles:
The last two forms of profiles (the one placing the two at the top; the other placing the two at the top and bottom) are especially useful
in the proofs of theorems involving IIA.
Arrow's IIA does not imply an IIA similar to those different from this at the top of this article nor conversely.
Historical Remark. In the first edition of his book, Arrow misinterpreted the IIA by considering the removal of a choice from the consideration set. Among the objects of choice, he distinguished those that by hypothesis are specified as feasible and infeasible. Consider two possible sets of voter orderings (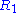
, ...,
) and (
, ...,
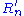) such that the ranking of X and Y for each voter i is the same for 
and 
. The voting rule generates corresponding social orderings R and R'. Now suppose that X and Y are feasible but Z is infeasible (say, the candidate is not on the ballot or the social state is outside the production possibility curve
). Arrow required that the voting rule that R and R' select the same (top-ranked) social choice from the feasible set (X, Y), and that this requirement holds no matter what the ranking is of infeasible Z relative to X and Y in the two sets of orderings. In fact, the IIA axiom does not allow "removing" an alternative from the available set (a candidate from the ballot). It says nothing about what would happen in such a case. All alternatives are assumed "feasible."
election, 5 voters rank 5 alternatives [A, B, C, D, E].
3 voters rank [A>B>C>D>E].
1 voter ranks [C>D>E>B>A].
1 voter ranks [E>C>D>B>A].
Borda count (a=0, b=1): C=13, A=12, B=11, D=8, E=6. C wins.
Now, the voter who ranks [C>D>E>B>A] instead ranks [C>B>E>D>A]; and the voter who ranks [E>C>D>B>A] instead ranks [E>C>B>D>A]. Note that they change their preferences only over the pairs [B, D] and [B, E].
The new Borda count: B=14, C=13, A=12, E=6, D=5. B wins.
Note that the social choice has changed the ranking of [B, A], [B, C] and [D, E]. The changes in the social choice ranking are dependent on irrelevant changes in the preference profile. In particular, B now wins instead of C, even though no voter changed their preference over [B, C].
Consider an election in which there are three candidates, A, B, and C, and only two voters. Each voter ranks the candidates in order of preference. The highest ranked candidate in a voter's preference is given 2 points, the second highest 1, and the lowest ranked 0; the overall ranking of a candidate is determined by the total score it gets; the highest ranked candidate wins.
We consider two profiles:
Thus, if the second voter wishes A to be elected, he had better vote ACB regardless of his actual opinion of C and B. This violates the idea of "independence of irrelevant alternatives" because the voter's comparative opinion of C and B affects whether A is elected or not. In both profiles, the rankings of A relative to B are the same for each voter, but the social rankings of A relative to B are different.
2 voters rank [A>B>C].
2 voters rank [C>B>A].
1 voter ranks [B>A>C].
Round 1: A=2, B=1, C=2; B eliminated.
Round 2: A=3, C=2; A wins.
Now, the two voters who rank [C>B>A] instead rank [B>C>A]. Note that they only change their preferences over B and C.
Round 1: A=2, B=3, C=0; C eliminated.
Round 2: A=2, B=3; B wins.
Note that the social choice ranking of [A, B] is dependent on preferences over the irrelevant alternatives [B, C].
7 voters rank 3 alternatives (A, B, C).
In an election, initially only A and B run: B wins with 4 votes to A's 3, but the entry of C into the race makes A the new winner.
The relative positions of A and B are reversed by the introduction of C, an "irrelevant" alternative.
. Polls leading up to the election suggested that, had the runoff been Edwin Edwards
v Buddy Roemer
, Roemer would have won. However, in the actual election, David Duke
managed to finish second and make the runoff instead of Roemer, a runoff which Edwards then won by a large margin. Thus, the presence of Duke in the election changed which of the non-Duke candidates won.
and the conditional logit models in econometrics
; outcomes that could theoretically violate this IIA (such as the outcome of multicandidate elections or any choice made by humans) may make multinomial logit and conditional logit invalid estimators.
IIA implies that adding another alternative or changing the characteristics of a third alternative does not affect the relative odds between the two alternatives considered. This implication is not realistic for applications with similar alternatives. Many examples have been constructed to illustrate this problem.
Consider the Red Bus/Blue Bus example. Commuters initially face a decision between two modes of transportation: car and red bus. Suppose that a consumer chooses between these two options with equal probability, 0.5, so that the odds ratio equals 1. Now suppose a third mode, blue bus, is added. Assuming bus commuters do not care about the color of the bus, consumers are expected to choose between bus and car still with equal probability, so the probability of car is still 0.5, while the probabilities of each of the two bus types is 0.25. But IIA implies that this is not the case: for the odds ratio between car and red bus to be preserved, the new probabilities must be: car 0.33; red bus 0.33; blue bus 0.33. In intuitive terms, the problem with the IIA axiom is that it leads to a failure to take account of the fact that red bus and blue bus are very similar, and are "perfect substitutes".
Many modeling advances have been motivated by a desire to alleviate the concerns raised by IIA. Generalized extreme value, multinomial probit
(also called conditional probit) and mixed logit
are alternative models for nominal outcomes which relax IIA, but these models often have assumptions of their own that may be difficult to meet or are computationally infeasible. The multinomial probit model has as a disadvantage that it makes calculation of maximum likelihood
infeasible for more than five alternatives as it involves multiple integrals. IIA can also be relaxed by specifying a hierarchical model, ranking the choice alternatives. The most popular of these is called the nested logit model.
Generalized extreme value and multinomial probit models possess another property, the Invariant Proportion of Substitution which suggests similarly counterintuitive individual choice behavior.
where p is a probability and
means that M is preferred over L. This axiom says that if one outcome (or lottery ticket) L is considered to be not as good as another (M), then having a chance with probability p of receiving L rather than N is considered to be not as good as having a chance with probability p of receiving M rather than N.
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
and various social sciences
Social sciences
Social science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
.
The word is used in different meanings in different contexts.
Although they all attempt to provide a rational account of individual behavior or aggregation of individual preferences,
the exact formulations differ from context to context.
In individual choice theory, the name "IIA" is sometimes used to refer to Chernoff
Herman Chernoff
Herman Chernoff is an American applied mathematician, statistician and physicist formerly a professor at MIT and currently working at Harvard University.-Education:* Ph.D., Applied Mathematics, 1948. Brown University....
's condition or Sen's property α (alpha):
if an alternative x chosen from a set T is an element of a subset S of T, then x must be chosen from S.
In social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
, Arrow's IIA is well known as one of the conditions in Arrow's impossibility theorem
Arrow's impossibility theorem
In social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
:
the social preferences between alternatives x and y depend only on the individual preferences between x and y.
Kenneth Arrow (1951) shows the impossibility of aggregating individual rank-order preferences ("votes") satisfying IIA and certain other reasonable conditions.
There are other requirements that go by the name of "IIA".
One such requirement is as follows:
If A is preferred to B out of the choice set {A,B}, then introducing a third alternative X, thus expanding the choice set to {A,B,X}, must not make B preferable to A.
In other words, preferences for A or B should not be changed by the inclusion of X, i.e., X is irrelevant to the choice between A and B. This formulation appears in bargaining theory, theories of individual choice
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, and voting theory. Some theorists find it too strict an axiom; experiments by Amos Tversky
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
, Daniel Kahneman
Daniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
, and others have shown that human behavior rarely adheres to this axiom.
A distinct formulation of IIA is found in social choice theory:
If A is selected over B out of the choice set {A,B} by a voting rule for given voter preferences of A, B, and an unavailable third alternative X, then B must not be selected over A by the voting rule if only preferences for X change.
In other words, whether A or B is selected should not be affected by a change in the vote for an unavailable X, which is thus irrelevant to the choice between A and B.
Voting theory
In voting systems, independence of irrelevant alternatives is often interpreted as, if one candidate (X) wins the election, and a new candidate (Y) is added to the ballot, only X or Y will win the election.Approval voting
Approval voting
Approval voting is a single-winner voting system used for elections. Each voter may vote for as many of the candidates as the voter wishes. The winner is the candidate receiving the most votes. Each voter may vote for any combination of candidates and may give each candidate at most one vote.The...
and range voting
Range voting
Range voting is a voting system for one-seat elections under which voters score each candidate, the scores are added up, and the candidate with the highest score wins.A form of range voting was apparently used in...
satisfy the independence of irrelevant alternatives criterion. Another cardinal system, cumulative voting
Cumulative voting
Cumulative voting is a multiple-winner voting system intended to promote more proportional representation than winner-take-all elections.- History :...
, does not satisfy the criterion.
An anecdote which illustrates a violation of this property has been attributed to Sidney Morgenbesser
Sidney Morgenbesser
Sidney Morgenbesser was a Columbia University philosopher. Born in New York City, he undertook philosophical study at the City College of New York and rabbinical study at the Jewish Theological Seminary of America, then pursued graduate study in philosophy at the University of Pennsylvania, where...
:
- After finishing dinner, Sidney Morgenbesser decides to order dessert. The waitress tells him he has two choices: apple pie and blueberry pie. Sidney orders the apple pie. After a few minutes the waitress returns and says that they also have cherry pie at which point Morgenbesser says "In that case I'll have the blueberry pie."
All voting systems have some degree of inherent susceptibility to strategic nomination
Strategic nomination
Strategic nomination is the manipulation of an election through its candidate set...
considerations. Some regard these considerations as less serious unless the voting system specifically fails the (easier to satisfy) independence of clones criterion
Independence of clones criterion
In voting systems theory, the independence of clones criterion measures an election method's robustness to strategic nomination. Nicolaus Tideman first formulated the criterion, which states that the addition of a candidate identical to one already present in an election will not cause the winner...
.
Local independence
A related criterion proposed by H. P. Young and A. Levenglick is called local independence of irrelevant alternatives. It says that if one candidate (X) would win an election, and a new alternative (Y) is added, X would still win if Y is not in the Smith setSmith set
In voting systems, the Smith set, named after John H. Smith, is the smallest non-empty set of candidates in a particular election such that each member beats every other candidate outside the set in a pairwise election. The Smith set provides one standard of optimal choice for an election outcome...
. In other words, the outcome of the election is independent of alternatives which are not in the Smith set. Note that this neither implies nor is implied by IIA; in fact, the two are mutually exclusive.
No deterministic ranked methods satisfy IIA, but local IIA is satisfied by some methods which always elect from the Smith set, such as ranked pairs
Ranked Pairs
Ranked pairs or the Tideman method is a voting system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences. RP can also be used to create a sorted list of winners....
and the Schulze method
Schulze method
The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners...
.
Criticism
IIA may be too strong a criterion for rank-order voting systems (e.g. the majority criterionMajority criterion
The majority criterion is a single-winner voting system criterion, used to compare such systems. The criterion states that "if one candidate is preferred by a majority of voters, then that candidate must win"....
). Consider
- 7 votes for A > B > C
- 6 votes for B > C > A
- 5 votes for C > A > B
then the net preference of the group under a majority criterion is that A wins over B, B wins over C, and C wins over A: these yield rock-paper-scissors
Rock-paper-scissors
Rock-paper-scissors is a hand game played by two people. The game is also known as roshambo, or another ordering of the three items ....
preferences for any pairwise comparison. For example, if B drops out of the race, the remaining votes will be:
- 7 votes for A > C
- 11 votes for C > A
Thus if a voting system satisfying the majority criterion selects any one of these, eliminating one of the candidates reverses the decision.
For example if the system chooses A, then if B drops out of the race, C will now win under the majority criterion, even though the change (B dropping out) concerned an "irrelevant" alternative candidate who did not win in the original circumstance. This is an example of the spoiler effect
Spoiler effect
The spoiler effect describes the effect a minor party candidate with little chance of winning has in a close election, when that candidate's presence in the election draws votes from a major candidate similar to them, thereby causing a candidate dissimilar to them to win the election...
.
In social choice
From Kenneth Arrow, each "voter" i in the society has an ordering Ri that ranks the (conceivable) objects of social choiceSocial choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
—x, y, and z in simplest case—from high to low.
An aggregation rule (voting rule) in turn maps each profile or tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(R1, ...,Rn) of voter preferences (orderings)
to a social ordering R that determines the social preference (ranking) of x, y, and z.
Arrow's IIA requires that whenever a pair of alternatives is ranked the same way in two preference profiles (over the same choice set), then the aggregation rule must order these two alternatives identically across the two profiles.
For example, suppose an aggregation rule ranks a above b at the profile given by
- (acbd, dbac),
(i.e., the first individual prefers a first, c second, b third, d last; the second individual prefers d first, ..., c last). Then, if it satisfies IIA, it must rank a above b at the following three profiles:
- (abcd, bdca)
- (abcd, bacd)
- (acdb, bcda).
The last two forms of profiles (the one placing the two at the top; the other placing the two at the top and bottom) are especially useful
in the proofs of theorems involving IIA.
Arrow's IIA does not imply an IIA similar to those different from this at the top of this article nor conversely.
Historical Remark. In the first edition of his book, Arrow misinterpreted the IIA by considering the removal of a choice from the consideration set. Among the objects of choice, he distinguished those that by hypothesis are specified as feasible and infeasible. Consider two possible sets of voter orderings (
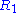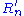, ..., ) and (, ...,) such that the ranking of X and Y for each voter i is the same for and . The voting rule generates corresponding social orderings R and R'. Now suppose that X and Y are feasible but Z is infeasible (say, the candidate is not on the ballot or the social state is outside the production possibility curveProduction possibility frontier
In economics, a production–possibility frontier , sometimes called a production–possibility curve or product transformation curve, is a graph that compares the production rates of two commodities that use the same fixed total of the factors of production...
). Arrow required that the voting rule that R and R' select the same (top-ranked) social choice from the feasible set (X, Y), and that this requirement holds no matter what the ranking is of infeasible Z relative to X and Y in the two sets of orderings. In fact, the IIA axiom does not allow "removing" an alternative from the available set (a candidate from the ballot). It says nothing about what would happen in such a case. All alternatives are assumed "feasible."
Borda count
In a Borda countBorda count
The Borda count is a single-winner election method in which voters rank candidates in order of preference. The Borda count determines the winner of an election by giving each candidate a certain number of points corresponding to the position in which he or she is ranked by each voter. Once all...
election, 5 voters rank 5 alternatives [A, B, C, D, E].
3 voters rank [A>B>C>D>E].
1 voter ranks [C>D>E>B>A].
1 voter ranks [E>C>D>B>A].
Borda count (a=0, b=1): C=13, A=12, B=11, D=8, E=6. C wins.
Now, the voter who ranks [C>D>E>B>A] instead ranks [C>B>E>D>A]; and the voter who ranks [E>C>D>B>A] instead ranks [E>C>B>D>A]. Note that they change their preferences only over the pairs [B, D] and [B, E].
The new Borda count: B=14, C=13, A=12, E=6, D=5. B wins.
Note that the social choice has changed the ranking of [B, A], [B, C] and [D, E]. The changes in the social choice ranking are dependent on irrelevant changes in the preference profile. In particular, B now wins instead of C, even though no voter changed their preference over [B, C].
Borda count and strategic voting
Consider an election in which there are three candidates, A, B, and C, and only two voters. Each voter ranks the candidates in order of preference. The highest ranked candidate in a voter's preference is given 2 points, the second highest 1, and the lowest ranked 0; the overall ranking of a candidate is determined by the total score it gets; the highest ranked candidate wins.
We consider two profiles:
- In profiles 1 and 2, the first voter casts his votes in the order BAC; so B receives 2 points, A receives 1, and C receives 0 from this voter.
- In profile 1, the second voter votes ACB, so A will win outright (the total scores: A 3, B 2, C 1).
- In profile 2, the second voter votes ABC, so A and B will tie (the total scores: A 3, B 3, C 0).
Thus, if the second voter wishes A to be elected, he had better vote ACB regardless of his actual opinion of C and B. This violates the idea of "independence of irrelevant alternatives" because the voter's comparative opinion of C and B affects whether A is elected or not. In both profiles, the rankings of A relative to B are the same for each voter, but the social rankings of A relative to B are different.
Instant-runoff voting
In an instant-runoff election, 5 voters rank 3 alternatives [A, B, C].2 voters rank [A>B>C].
2 voters rank [C>B>A].
1 voter ranks [B>A>C].
Round 1: A=2, B=1, C=2; B eliminated.
Round 2: A=3, C=2; A wins.
Now, the two voters who rank [C>B>A] instead rank [B>C>A]. Note that they only change their preferences over B and C.
Round 1: A=2, B=3, C=0; C eliminated.
Round 2: A=2, B=3; B wins.
Note that the social choice ranking of [A, B] is dependent on preferences over the irrelevant alternatives [B, C].
Plurality voting system
In a plurality voting systemPlurality voting system
The plurality voting system is a single-winner voting system often used to elect executive officers or to elect members of a legislative assembly which is based on single-member constituencies...
7 voters rank 3 alternatives (A, B, C).
- 3 voters rank (A>B>C)
- 2 voters rank (B>A>C)
- 2 voters rank (C>B>A)
In an election, initially only A and B run: B wins with 4 votes to A's 3, but the entry of C into the race makes A the new winner.
The relative positions of A and B are reversed by the introduction of C, an "irrelevant" alternative.
Two-round system
A probable example of the two-round system's failing this criterion was the 1991 Louisiana gubernatorial electionLouisiana gubernatorial election, 1991
The Louisiana gubernatorial election of 1991 resulted in the election of Edwin Edwards to his fourth non-consecutive term as governor of Louisiana...
. Polls leading up to the election suggested that, had the runoff been Edwin Edwards
Edwin Edwards
Edwin Washington Edwards served as the Governor of Louisiana for four terms , twice as many terms as any other Louisiana chief executive has served. Edwards was also Louisiana's first Roman Catholic governor in the 20th century...
v Buddy Roemer
Buddy Roemer
Charles Elson "Buddy" Roemer III is an American politician who served as the 52nd Governor of Louisiana, from 1988 to 1992. He was elected as a Democrat but switched to the Republican Party on March 11, 1991...
, Roemer would have won. However, in the actual election, David Duke
David Duke
David Ernest Duke is a former Grand Wizard of the Knights of the Ku Klux Klan an American activist and writer, and former Republican Louisiana State Representative. He was also a former candidate in the Republican presidential primaries in 1992, and in the Democratic presidential primaries in...
managed to finish second and make the runoff instead of Roemer, a runoff which Edwards then won by a large margin. Thus, the presence of Duke in the election changed which of the non-Duke candidates won.
In econometrics
IIA is a property of the multinomial logitMultinomial logit
In statistics, economics, and genetics, a multinomial logit model, also known as multinomial logistic regression, is a regression model which generalizes logistic regression by allowing more than two discrete outcomes...
and the conditional logit models in econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
; outcomes that could theoretically violate this IIA (such as the outcome of multicandidate elections or any choice made by humans) may make multinomial logit and conditional logit invalid estimators.
IIA implies that adding another alternative or changing the characteristics of a third alternative does not affect the relative odds between the two alternatives considered. This implication is not realistic for applications with similar alternatives. Many examples have been constructed to illustrate this problem.
Consider the Red Bus/Blue Bus example. Commuters initially face a decision between two modes of transportation: car and red bus. Suppose that a consumer chooses between these two options with equal probability, 0.5, so that the odds ratio equals 1. Now suppose a third mode, blue bus, is added. Assuming bus commuters do not care about the color of the bus, consumers are expected to choose between bus and car still with equal probability, so the probability of car is still 0.5, while the probabilities of each of the two bus types is 0.25. But IIA implies that this is not the case: for the odds ratio between car and red bus to be preserved, the new probabilities must be: car 0.33; red bus 0.33; blue bus 0.33. In intuitive terms, the problem with the IIA axiom is that it leads to a failure to take account of the fact that red bus and blue bus are very similar, and are "perfect substitutes".
Many modeling advances have been motivated by a desire to alleviate the concerns raised by IIA. Generalized extreme value, multinomial probit
Multinomial probit
In econometrics and statistics, the multinomial probit model, a popular alternative to the multinomial logit model, is a generalization of the probit model that allows more than two discrete, unordered outcomes. It is not to be confused with the multivariate probit model, which is used to model...
(also called conditional probit) and mixed logit
Mixed logit
Mixed logit is a fully general statistical model for examining discrete choices. The motivation for the mixed logit model arises from the limitations of the standard logit model...
are alternative models for nominal outcomes which relax IIA, but these models often have assumptions of their own that may be difficult to meet or are computationally infeasible. The multinomial probit model has as a disadvantage that it makes calculation of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
infeasible for more than five alternatives as it involves multiple integrals. IIA can also be relaxed by specifying a hierarchical model, ranking the choice alternatives. The most popular of these is called the nested logit model.
Generalized extreme value and multinomial probit models possess another property, the Invariant Proportion of Substitution which suggests similarly counterintuitive individual choice behavior.
Choice under uncertainty
In the expected utility theory of von Neumann and Morgenstern, four axioms together imply that individuals act in situations of risk as if they maximize the expected value of a utility function. One of the axioms is a version of the IIA axiom:- If
, then for any 
and 
,
where p is a probability and
means that M is preferred over L. This axiom says that if one outcome (or lottery ticket) L is considered to be not as good as another (M), then having a chance with probability p of receiving L rather than N is considered to be not as good as having a chance with probability p of receiving M rather than N.See also
- Luce's choice axiomLuce's choice axiomIn probability theory, Luce's choice axiom, formulated by R. Duncan Luce , states that the probability of selecting one item over another from a pool of many items is not affected by the presence or absence of other items in the pool...
- Menu dependenceMenu dependenceRoughly speaking, in decision theory, game theory, and rational choice, menu dependence arises when the evaluation of alternatives for choice or the mode of selection guiding choice varies parametrically with what collection of alternatives is available for choice...
- Monty Hall problem, in which an seemingly-unrelated piece of information makes a difference to a choice
External links
- Steven Callander and Catherine H.Wilson, "Context-dependent Voting," Quarterly Journal of Political Science, 2006, 1: 227–254
- Thomas J. Steenburgh, (2008) "Invariant Proportion of Substitution Property (IPS) of Discrete-Choice Models," Marketing Science, Vol. 27, No. 2, pp. 300–307.