Rarita-Schwinger equation
Encyclopedia
In theoretical physics
, the Rarita–Schwinger equation is the
relativistic
field equation
of spin
-3/2 fermion
s. It is similar to the Dirac equation
for spin-1/2 fermions. This equation was first introduced by William Rarita
and Julian Schwinger
in 1941. In modern notation it can be written as: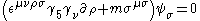
where
is the Levi-Civita symbol
,
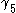and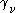 
are Dirac matrices, 
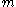is the mass, 
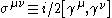, and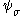 
is a vector-valued spinor
with additional components compared to the four component spinor in the Dirac equation. It corresponds to the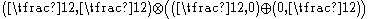
representation of the Lorentz group
, or rather, its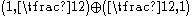
part.
This field equation can be derived as the Euler–Lagrange equation corresponding to the Rarita-Schwinger Lagrangian
:
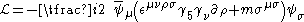
where the bar above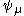
denotes the Dirac adjoint.
This equation is useful for the wave function of composite objects like , Delta
(Δ) baryon
s or for the hypothetical gravitino
. So far, no fundamental particle with spin 3/2 has been found experiment
ally.
The massless Rarita–Schwinger equation has a gauge symmetry, under the gauge transformation of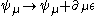
, where 
is an arbitrary spinor field.
"Weyl" and "Majorana" versions of the Rarita–Schwinger equation also exist.
:
.
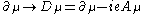In 1969, Velo and Zwanziger showed that the Rarita–Schwinger lagrangian coupled to electromagnetism
leads to equation with solutions representing wavefronts, some of which propagate faster than light. In other words,
the field then suffers from acausal, superluminal propagation; consequently, the quantization
in interaction with electromagnetism is essentially flawed.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Rarita–Schwinger equation is the
relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
field equation
Field equation
A field equation is an equation in a physical theory that describes how a fundamental force interacts with matter...
of spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
-3/2 fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s. It is similar to the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
for spin-1/2 fermions. This equation was first introduced by William Rarita
William Rarita
William Rarita was an American theoretical physicist who mainly worked on nuclear physics, particle physics and relativistic quantum mechanics. He is particularly famous for the formulation of Rarita-Schwinger equation. His famous formula is applicable to spin 3/2 particles as opposed to spin 1/2...
and Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
in 1941. In modern notation it can be written as:
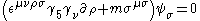
where
is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
,
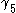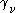and are Dirac matrices, 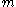is the mass, 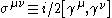, and 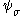is a vector-valued spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
with additional components compared to the four component spinor in the Dirac equation. It corresponds to the
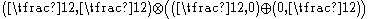representation of the Lorentz groupRepresentations of the Lorentz group
The Lorentz group of theoretical physics has a variety of representations, corresponding to particles with integer and half-integer spins in quantum field theory. These representations are normally constructed out of spinors....
, or rather, its
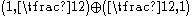part.This field equation can be derived as the Euler–Lagrange equation corresponding to the Rarita-Schwinger Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
:
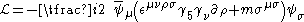
where the bar above
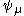denotes the Dirac adjoint.This equation is useful for the wave function of composite objects like , Delta
Delta baryon
The Delta baryons are a family of subatomic hadron particles which have the symbols , , , and and electric charges +2, +1, 0 and -1 elementary charge respectively...
(Δ) baryon
Baryon
A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
s or for the hypothetical gravitino
Gravitino
The gravitino is the supersymmetric partner of the graviton, as predicted by theories combining general relativity and supersymmetry; i.e. supergravity theories...
. So far, no fundamental particle with spin 3/2 has been found experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
ally.
The massless Rarita–Schwinger equation has a gauge symmetry, under the gauge transformation of
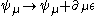, where is an arbitrary spinor field."Weyl" and "Majorana" versions of the Rarita–Schwinger equation also exist.
Drawbacks of the equation
The current description of massive, higher spin fields through either Rarita-Schwinger or Fierz-Pauli formalisms is afflicted with several maladies. As in the case of the Dirac equation, electromagnetic interaction can be added by promoting the partial derivative to gauge covariant derivativeGauge covariant derivative
The gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
:
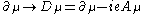.In 1969, Velo and Zwanziger showed that the Rarita–Schwinger lagrangian coupled to electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
leads to equation with solutions representing wavefronts, some of which propagate faster than light. In other words,
the field then suffers from acausal, superluminal propagation; consequently, the quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
in interaction with electromagnetism is essentially flawed.