Gauge covariant derivative
Encyclopedia
The gauge covariant derivative (icon) is like a generalization of the covariant derivative
used in general relativity
. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations. Likewise, the gauge covariant derivative is the ordinary derivative modified in such a way as to make it behave like a true vector operator, so that equations written using the covariant derivative preserve their physical properties under gauge transformations.
, the gauge covariant derivative of a fluid may be defined as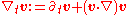
where
is a velocity vector field
of a fluid.
, which studies a particular class of fields
which are of importance in quantum field theory
, the minimally-coupled
gauge covariant derivative is defined as
where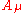
is the electromagnetic vector potential
.
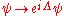
and for the gauge potential
then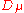
transforms as
,
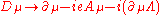and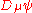
transforms as
and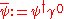
transforms as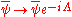
so that
and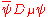
in the QED Lagrangian
is therefore gauge invariant, and the gauge covariant derivative is thus named aptly.
On the other hand, the non-covariant derivative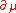
would not preserve the Lagrangian's gauge symmetry, since
.
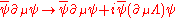, the gauge covariant derivative is http://www.fuw.edu.pl/~dobaczew/maub-42w/node9.html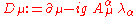
where
is the coupling constant
,
is the gluon gauge field, for eight different gluons 
, 
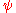is a four-component Dirac spinor, and where 
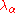is one of the eight Gell-Mann matrices
,
.
, the gauge covariant derivative is defined as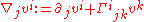
where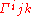
is the Christoffel symbol.
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
used in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations. Likewise, the gauge covariant derivative is the ordinary derivative modified in such a way as to make it behave like a true vector operator, so that equations written using the covariant derivative preserve their physical properties under gauge transformations.
Fluid dynamics
In fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the gauge covariant derivative of a fluid may be defined as
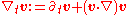
where
is a velocity vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
of a fluid.
Gauge theory
In gauge theoryGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, which studies a particular class of fields
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
which are of importance in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the minimally-coupled
Minimal coupling
In physics, minimal coupling refers to a coupling between fields which involves only the charge distribution and not higher multipole moments of the charge distribution...
gauge covariant derivative is defined as
where
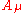is the electromagnetic vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
.
What happens to the covariant derivative under a gauge transformation
If a gauge transformation is given by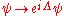and for the gauge potential
then
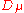transforms as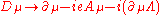,and
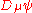transforms asand
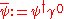transforms as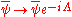so that
and
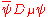in the QED LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
is therefore gauge invariant, and the gauge covariant derivative is thus named aptly.
On the other hand, the non-covariant derivative
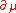would not preserve the Lagrangian's gauge symmetry, since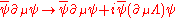.Quantum chromodynamics
In quantum chromodynamicsQuantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, the gauge covariant derivative is http://www.fuw.edu.pl/~dobaczew/maub-42w/node9.html
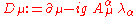
where
is the coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
,
is the gluon gauge field, for eight different gluons , 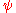is a four-component Dirac spinor, and where 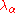is one of the eight Gell-Mann matricesGell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
,
.General relativity
In general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the gauge covariant derivative is defined as
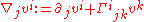
where
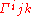is the Christoffel symbol.