Rasch model estimation
Encyclopedia
Estimation of a Rasch model is used to estimate the parameters of the Rasch model
. Various techniques are employed to estimate the parameters from matrices of response data. The most common approaches are types of maximum likelihood
estimation, such as joint and conditional maximum likelihood estimation. Joint maximum likelihood (JML) equations are efficient, but inconsistent for a finite number of items, whereas conditional maximum likelihood (CML) equations give consistent and unbiased item estimates. Person estimates are generally thought to have bias
associated with them, although weighted likelihood estimation methods for the estimation of person parameters reduce the bias.
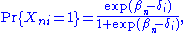
where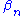
is the ability of person 
and 
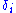is the difficulty of item 
.
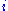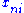denote the observed response for person n on item i. The probability of the observed data matrix, which is the product of the probabilities of the individual responses, is given by the likelihood function
The log-likelihood function is then
where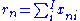
is the total raw score for person n, 
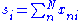is the total raw score for item i, N is the total number of persons and I is the total number of items.
Solution equations are obtained by taking partial derivatives with respect to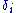
and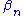 
and setting the result equal to 0. The JML solution equations are:
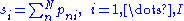
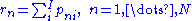
where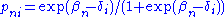
. A more accurate estimate of each 
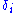is obtained by multiplying the estimates by 
.
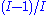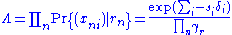
in which
Rasch model
Rasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
. Various techniques are employed to estimate the parameters from matrices of response data. The most common approaches are types of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimation, such as joint and conditional maximum likelihood estimation. Joint maximum likelihood (JML) equations are efficient, but inconsistent for a finite number of items, whereas conditional maximum likelihood (CML) equations give consistent and unbiased item estimates. Person estimates are generally thought to have bias
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
associated with them, although weighted likelihood estimation methods for the estimation of person parameters reduce the bias.
Rasch model
The Rasch model for dichotomous data takes the form: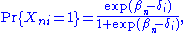where
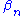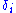is the ability of person and is the difficulty of item 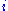.Joint maximum likelihood
Let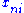 denote the observed response for person n on item i. The probability of the observed data matrix, which is the product of the probabilities of the individual responses, is given by the likelihood functionThe log-likelihood function is then
where
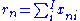is the total raw score for person n, 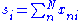is the total raw score for item i, N is the total number of persons and I is the total number of items.Solution equations are obtained by taking partial derivatives with respect to
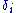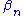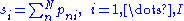
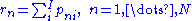
and and setting the result equal to 0. The JML solution equations are:where
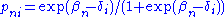. A more accurate estimate of each 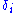is obtained by multiplying the estimates by 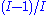.Conditional maximum likelihood
The conditional likelihood function is defined as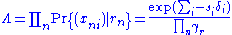in which
-
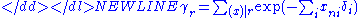
is the elementary symmetric function of order r, which represents the sum over all combinations of r items. For example, in the case of three items,
Estimation algorithms
Some kind of expectation-maximization algorithmExpectation-maximization algorithmIn statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
is used in the estimation of the parameters of Rasch models. Algorithms for implementing Maximum Likelihood estimation commonly employ Newton-Raphson iterations to solve for solution equations obtained from setting the partial derivatives of the log-likelihood functions equal to 0. Convergence criteria are used to determine when the iterations cease. For example, the criterion might be that the mean item estimate changes by less than a certain value, such as 0.001, between one iteration and another for all items.
See also
- Expectation-maximization algorithmExpectation-maximization algorithmIn statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
- Rasch modelRasch modelRasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
-
