Rasch model
Encyclopedia
Rasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to capital punishment from responses on a questionnaire.
Rasch models are particularly used in psychometrics
, the field concerned with the theory and technique of psychological and educational measurement. In addition, they are increasingly being used in other areas, including the health profession
and market research because of their general applicability.
The mathematical theory underlying Rasch models is in some respects the same as item response theory
. However, proponents of Rasch models argue it has a specific property that provides a criterion for successful measurement. Application of the models provides diagnostic information regarding how well the criterion is met. Application of the models can also provide information about how well items or questions on assessments work to measure the ability or trait. Prominent advocates of Rasch models include Benjamin D Wright, David Andrich
and Erling Andersen.
of the difference between the person and item parameter. The mathematical form of the model is provided later in this article. In most contexts, the parameters of the model pertain to the level of a quantitative trait possessed by a person or item. For example, in educational tests, item parameters pertain to the difficulty of items while person parameters pertain to the ability or attainment level of people who are assessed. The higher a person's ability relative to the difficulty of an item, the higher the probability of a correct response on that item. When a person's location on the latent trait is equal to the difficulty of the item, there is by definition a 0.5 probability of a correct response in the Rasch model.
The purpose of applying the model is to obtain measurements from categorical response data. Estimation methods are used to obtain estimates from matrices of response data based on the model.
The Rasch model is a model in the sense that it represents the structure which data should exhibit in order to obtain measurements from the data; i.e. it provides a criterion for successful measurement. It is therefore a model in the sense of an ideal or standard. The perspective or paradigm underpinning the Rasch model is distinctly different from the perspective underpinning statistical modelling. Models are most often used with the intention of describing a set of data. Parameters are modified and accepted or rejected based on how well they fit the data. In contrast, when the Rasch model is employed, the objective is to obtain data which fit the model (Andrich, 2004). The rationale for this perspective is that the Rasch model embodies requirements which must be met in order to obtain measurement, in the sense that measurement is generally understood in the physical sciences.
A useful analogy for understanding this rationale is to consider objects measured on a weighing scale. Suppose the weight of an object A is measured as being substantially greater than the weight of an object B on one occasion, then immediately afterward the weight of object B is measured as being substantially greater than the weight of object A. A property we require of measurements is that the resulting comparison between objects should be the same, or invariant, irrespective of other factors. This key requirement is embodied within the formal structure of the Rasch model. Consequently, the Rasch model is not altered to suit data. Instead, the method of assessment should be changed so that this requirement is met, in the same way that a weighing scale should be rectified if it gives different comparisons between objects upon separate measurements of the objects.
Data analysed using the model are usually responses to conventional items on tests, such as educational tests with right/wrong answers. However, the model is a general one, and can be applied wherever discrete data are obtained with the intention of measuring a quantitative attribute or trait.
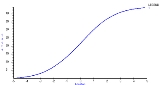
When all test-takers have an opportunity to attempt all items on a single test, each total score on the test maps to a unique estimate of ability and the greater the total, the greater the ability estimate. Total scores do not have a linear relationship with ability estimates. Rather, the relationship is non-linear as shown in Figure 1. The total score is shown on the vertical axis, while the corresponding person location estimate is shown on the horizontal axis. For the particular test on which the test characteristic curve (TCC) shown in Figure 1 is based, the relationship is approximately linear throughout the range of total scores from about 10 to 33. The shape of the TCC is generally somewhat sigmoid as in this example. However, the precise relationship between total scores and person location estimates depends on the distribution of items on the test. The TCC is steeper in ranges on the continuum in which there are a number of items, such as in the range on either side of 0 in Figures 1 and 2.
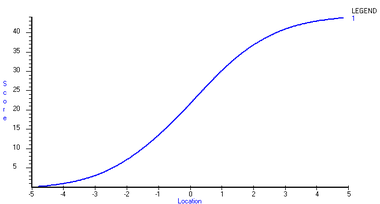
In applying the Rasch model, item locations are often scaled first, based on methods such as those described below. This part of the process of scaling is often referred to as item calibration. In educational tests, the smaller the proportion of correct responses, the higher the difficulty of an item and hence the higher the item's scale location. Once item locations are scaled, the person locations are measured on the scale. As a result, person and item locations are estimated on a single scale as shown in Figure 2.
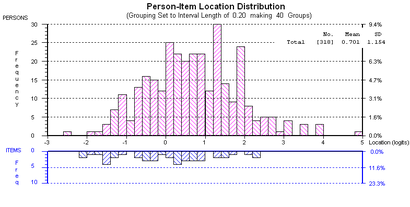For dichotomous data such as right/wrong answers, by definition, the location of an item on a scale corresponds with the person location at which there is a 0.5 probability of a correct response to the question. In general, the probability of a person responding correctly to a question with difficulty lower than that person's location is greater than 0.5, while the probability of responding correctly to a question with difficulty greater than the person's location is less than 0.5. The Item Characteristic Curve (ICC) or Item Response Function (IRF) shows the probability of a correct response as a function of the ability of persons. A single ICC is shown and explaind in more detail in relation to Figure 4 in this article (see also the item response function). The leftmost ICCs in Figure 3 are the easiest items, the rightmost items in the same figure are the most difficult items.
When responses of a person are listed according to item difficulty, from lowest to highest, the most likely pattern is a Guttman pattern
or vector; i.e. {1,1,...,1,0,0,0,...,0}. However, while this pattern is the most probable given the structure of the Rasch model, the model requires only probabilistic Guttman response patterns; that is, patterns which tend toward the Guttman pattern. It is unusual for responses to conform strictly to the pattern because there are many possible patterns. It is unnecessary for responses to conform strictly to the pattern in order for data to fit the Rasch model.
Each ability estimate has an associated standard error of measurement, which quantifies the degree of uncertainty associated with the ability estimate. Item estimates also have standard errors. Generally, the standard errors of item estimates are considerably smaller than the standard errors of person estimates because there are usually more response data for an item than for a person. That is, the number of people attempting a given item is usually greater than the number of items attempted by a given person. Standard errors of person estimates are smaller where the slope of the TCC is steeper, which is generally through the middle range of scores on a test. Thus, there is greater precision in this range since the steeper the slope, the greater the distinction between any two points on the line.
Statistical and graphical tests are used to evaluate the correspondence of data with the model. Certain tests are global, while others focus on specific items or people. Certain tests of fit provide information about which items can be used to increase the reliability
of a test by omitting or correcting problems with poor items. In Rasch Measurement the person separation index is used instead of reliability indices. However, the person separation index is analogous to a reliability index. The separation index is a summary of the genuine separation as a ratio to separation including measurement error. As mentioned earlier, the level of measurement error is not uniform across the range of a test, but is generally larger for more extreme scores (low and high).
, a Danish mathematician and statistician who advanced the epistemological case for the models based on their congruence with a core requirement of measurement in physics
; namely the requirement of invariant comparison. This is the defining feature of the class of models, as is elaborated upon in the following section. The Rasch model for dichotomous data has a close conceptual relationship to the law of comparative judgment
(LCJ), a model formulated and used extensively by L. L. Thurstone (cf Andrich, 1978b), and therefore also to the Thurstone scale
.
Prior to introducing the measurement model he is best known for, Rasch had applied the Poisson distribution
to reading data as a measurement model, hypothesizing that in the relevant empirical context, the number of errors made by a given individual was governed by the ratio of the text difficulty to the person's reading ability. Rasch referred to this model as the multiplicative Poisson model. Rasch's model for dichotomous data – i.e. where responses are classifiable into two categories – is his most widely known and used model, and is the main focus here. This model has the form of a simple logistic function
.
The brief outline above highlights certain distinctive and interrelated features of Rasch's perspective on social measurement, which are as follows:
Thus, congruent with the perspective articulated by Thomas Kuhn
in his 1961 paper The function of measurement in modern physical science, measurement was regarded both as being founded in theory
, and as being instrumental to detecting quantitative anomalies incongruent with hypotheses related to a broader theoretical framework. This perspective is in contrast to that generally prevailing in the social sciences, in which data such as test scores are directly treated as measurements without requiring a theoretical foundation for measurement. Although this contrast exists, Rasch's perspective is actually complementary to the use of statistical analysis or modelling that requires interval-level measurements, because the purpose of applying the Rasch model is to obtain such measurements. Applications of the Rasch model are described in Sivakumar, Durtis & Hungi (2005).
(IRT) model with one item parameter. However, rather than being a particular IRT model, proponents of the model regard it as a model that possesses a property which distinguishes it from other IRT models. Specifically, the defining property of Rasch models is their formal or mathematical embodiment of the principle of invariant comparison
. Rasch summarised the principle of invariant comparison as follows:
Rasch models embody this principle because their formal structure permits algebraic separation of the person and item parameters, in the sense that the person parameter can be eliminated during the process of statistical estimation of item parameters. This result is achieved through the use of conditional maximum likelihood
estimation, in which the response space is partitioned according to person total scores. The consequence is that the raw score for an item or person is the sufficient statistic for the item or person parameter
. That is to say, the person total score contains all information available within the specified context about the individual, and the item total score contains all information with respect to item, with regard to the relevant latent trait. The Rasch model requires a specific structure in the response data, namely a probabilistic Guttman
structure.
In somewhat more familiar terms, Rasch models provide a basis and justification for obtaining person locations on a continuum from total scores on assessments. Although it is not uncommon to treat total scores directly as measurements, they are actually counts of discrete observations rather than measurements. Each observation represents the observable outcome of a comparison
between a person and item. Such outcomes are directly analogous to the observation of the rotation of a balance scale in one direction or another. This observation would indicate that one or other object has a greater mass, but counts of such observations cannot be treated directly as measurements.
Rasch pointed out that the principle of invariant comparison is characteristic of measurement in physics using, by way of example, a two-way experimental frame of reference in which each instrument exerts a mechanical
force
upon solid bodies to produce acceleration
. Rasch (1960/1980, pp. 112–3) stated of this context: "Generally: If for any two objects we find a certain ratio of their accelerations produced by one instrument, then the same ratio will be found for any other of the instruments". It is readily shown that Newton's second law entails that such ratios are inversely proportional to the ratios of the masses
of the bodies.
be a dichotomous random variable where, for example, 
denotes a correct response and 
an incorrect response to a given assessment item. In the Rasch model for dichotomous data, the probability of the outcome 
is given by:
where
is the ability of person 
and 
is the difficulty of item 
. Thus, in the case of a dichotomous attainment item, 
is the probability of success upon interaction between the relevant person and assessment item. It is readily shown that the log odds
, or logit
, of correct response by a person to an item, based on the model, is equal to
. It can be shown that the log odds of a correct response by a person to one item, conditional on a correct response to one of two items, is equal to the difference between the item locations. For example,
where
is the total score of person n over the two items, which implies a correct response to one or other of the items. Hence, the conditional log odds does not involve the person parameter 
, which can therefore be eliminated by conditioning on the total score 
. That is, by partitioning the responses according to raw scores and calculating the log odds of a correct response, an estimate 
is obtained without involvement of 
. More generally, a number of item parameters can be estimated iteratively through application of a process such as Conditional Maximum Likelihood estimation (see Rasch model estimation
). While more involved, the same fundamental principle applies in such estimations.
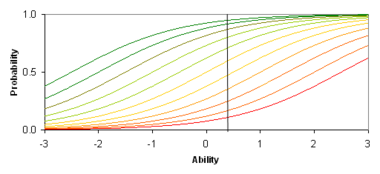
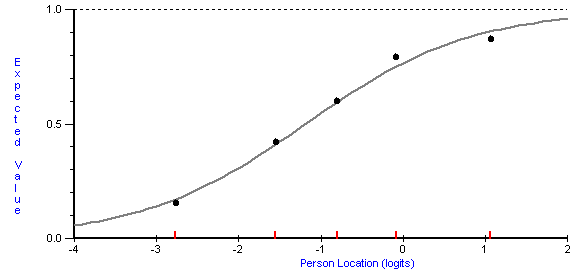The ICC of the Rasch model for dichotomous data is shown in Figure 4. The grey line maps a person with a location of approximately 0.2 on the latent continuum, to the probability of the discrete outcome 
for items with different locations on the latent continuum. The location of an item is, by definition, that location at which the probability that 
is equal to 0.5. In figure 4, the black circles represent the actual or observed proportions of persons within Class Intervals for which the outcome was observed. For example, in the case of an assessment item used in the context of educational psychology
, these could represent the proportions of persons who answered the item correctly. Persons are ordered by the estimates of their locations on the latent continuum and classified into Class Intervals on this basis in order to graphically inspect the accordance of observations with the model. There is a close conformity of the data with the model. In addition to graphical inspection of data, a range of statistical tests of fit are used to evaluate whether departures of observations from the model can be attributed to random effects alone, as required, or whether there are systematic departures from the model.
In the two-parameter logistic model (2PL-IRT; Lord & Novick, 1968) the weighted raw score is theoretically sufficient for person parameters, where the weights are given by model parameters referred to as discrimination parameters. Lord & Novick's one-parameter logistic model, 1PL, appears similar to the Rasch model in that it does not have discrimination parameters, but 1PL has different motivation and subtly different parameterization. The 1PL is a descriptive model which summarizes the sample as a normal distribution. The dichotomous Rasch model is a measurement model which parameterizes each member of the sample individually. There are other technical differences.
Verhelst & Glas (1995) derive Conditional Maximum Likelihood (CML) equations for a model they refer to as the One Parameter Logistic Model (OPLM). In algebraic form it appears to be identical with the 2PL model, but OPLM contains preset discrimination indexes rather than 2PL's estimated discrimination parameters. As noted by these authors, though, the problem one faces in estimation with estimated discrimination parameters is that the discriminations are unknown, meaning that the weighted raw score "is not a mere statistic, and hence it is impossible to use CML as an estimation method" (Verhelst & Glas, 1995, p. 217). That is, sufficiency of the weighted "score" in the 2PL cannot be used according to the way in which a sufficient statistic is defined. If the weights are imputed instead of being estimated, as in OPLM, conditional estimation is possible and the properties of the Rasch model are retained (Verhelst, Glas & Verstralen, 1995; Verhelst & Glas, 1995). In OPLM, the values of the discrimination index are restricted to between 1 and 15. A limitation of this approach is that in practice, values of discrimination indexes must be preset as a starting point. This means some type of estimation of discrimination is involved when the purpose is to avoid doing so.
The Rasch model for dichotomous data inherently entails a single discrimination parameter which, as noted by Rasch (1960/1980, p. 121), constitutes an arbitrary choice of the unit
in terms of which magnitudes of the latent trait are expressed or estimated. However, the Rasch model requires that the discrimination is uniform across interactions between persons and items within a specified frame of reference (i.e. the assessment context given conditions for assessment).
Rasch models are particularly used in psychometrics
Psychometrics
Psychometrics is the field of study concerned with the theory and technique of psychological measurement, which includes the measurement of knowledge, abilities, attitudes, personality traits, and educational measurement...
, the field concerned with the theory and technique of psychological and educational measurement. In addition, they are increasingly being used in other areas, including the health profession
Health profession
The health care industry, or medical industry, is the sector of the economic system that provides goods and services to treat patients with curative, preventive, rehabilitative, palliative, or, at times, unnecessary care...
and market research because of their general applicability.
The mathematical theory underlying Rasch models is in some respects the same as item response theory
Item response theory
In psychometrics, item response theory also known as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is based...
. However, proponents of Rasch models argue it has a specific property that provides a criterion for successful measurement. Application of the models provides diagnostic information regarding how well the criterion is met. Application of the models can also provide information about how well items or questions on assessments work to measure the ability or trait. Prominent advocates of Rasch models include Benjamin D Wright, David Andrich
David Andrich
David Andrich has made substantial contributions to quantitative social science including seminal work on the Polytomous Rasch model for measurement, which is used in the social sciences, in health and other areas. He is currently a Winthrop Professor at the University of Western Australia, where...
and Erling Andersen.
The Rasch model for measurement
In the Rasch model, the probability of a specified response (e.g. right/wrong answer) is modeled as a function of person and item parameters. Specifically, in the simple Rasch model, the probability of a correct response is modeled as a logistic functionLogistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
of the difference between the person and item parameter. The mathematical form of the model is provided later in this article. In most contexts, the parameters of the model pertain to the level of a quantitative trait possessed by a person or item. For example, in educational tests, item parameters pertain to the difficulty of items while person parameters pertain to the ability or attainment level of people who are assessed. The higher a person's ability relative to the difficulty of an item, the higher the probability of a correct response on that item. When a person's location on the latent trait is equal to the difficulty of the item, there is by definition a 0.5 probability of a correct response in the Rasch model.
The purpose of applying the model is to obtain measurements from categorical response data. Estimation methods are used to obtain estimates from matrices of response data based on the model.
The Rasch model is a model in the sense that it represents the structure which data should exhibit in order to obtain measurements from the data; i.e. it provides a criterion for successful measurement. It is therefore a model in the sense of an ideal or standard. The perspective or paradigm underpinning the Rasch model is distinctly different from the perspective underpinning statistical modelling. Models are most often used with the intention of describing a set of data. Parameters are modified and accepted or rejected based on how well they fit the data. In contrast, when the Rasch model is employed, the objective is to obtain data which fit the model (Andrich, 2004). The rationale for this perspective is that the Rasch model embodies requirements which must be met in order to obtain measurement, in the sense that measurement is generally understood in the physical sciences.
A useful analogy for understanding this rationale is to consider objects measured on a weighing scale. Suppose the weight of an object A is measured as being substantially greater than the weight of an object B on one occasion, then immediately afterward the weight of object B is measured as being substantially greater than the weight of object A. A property we require of measurements is that the resulting comparison between objects should be the same, or invariant, irrespective of other factors. This key requirement is embodied within the formal structure of the Rasch model. Consequently, the Rasch model is not altered to suit data. Instead, the method of assessment should be changed so that this requirement is met, in the same way that a weighing scale should be rectified if it gives different comparisons between objects upon separate measurements of the objects.
Data analysed using the model are usually responses to conventional items on tests, such as educational tests with right/wrong answers. However, the model is a general one, and can be applied wherever discrete data are obtained with the intention of measuring a quantitative attribute or trait.
Scaling
In applying the Rasch model, item locations are often scaled first, based on methods such as those described below. This part of the process of scaling is often referred to as item calibration. In educational tests, the smaller the proportion of correct responses, the higher the difficulty of an item and hence the higher the item's scale location. Once item locations are scaled, the person locations are measured on the scale. As a result, person and item locations are estimated on a single scale as shown in Figure 2.
Interpreting scale locations
When responses of a person are listed according to item difficulty, from lowest to highest, the most likely pattern is a Guttman pattern
Guttman scale
In statistical surveys conducted by means of structured interviews or questionnaires, a subset of the survey items having binary answers forms a Guttman scale if they can be ranked in some order so that, for a rational respondent, the response pattern can be captured by a single index on that...
or vector; i.e. {1,1,...,1,0,0,0,...,0}. However, while this pattern is the most probable given the structure of the Rasch model, the model requires only probabilistic Guttman response patterns; that is, patterns which tend toward the Guttman pattern. It is unusual for responses to conform strictly to the pattern because there are many possible patterns. It is unnecessary for responses to conform strictly to the pattern in order for data to fit the Rasch model.
Statistical and graphical tests are used to evaluate the correspondence of data with the model. Certain tests are global, while others focus on specific items or people. Certain tests of fit provide information about which items can be used to increase the reliability
Reliability (statistics)
In statistics, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error.-Types:There are several general classes of reliability estimates:...
of a test by omitting or correcting problems with poor items. In Rasch Measurement the person separation index is used instead of reliability indices. However, the person separation index is analogous to a reliability index. The separation index is a summary of the genuine separation as a ratio to separation including measurement error. As mentioned earlier, the level of measurement error is not uniform across the range of a test, but is generally larger for more extreme scores (low and high).
Features of the Rasch model
The class of models is named after Georg RaschGeorg Rasch
Georg Rasch was a Danish mathematician, statistician, and psychometrician, most famous for the development of a class of measurement models known as Rasch models. He studied with R.A. Fisher and also briefly with Ragnar Frisch, and was elected a member of the International Statistical Institute in...
, a Danish mathematician and statistician who advanced the epistemological case for the models based on their congruence with a core requirement of measurement in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
; namely the requirement of invariant comparison. This is the defining feature of the class of models, as is elaborated upon in the following section. The Rasch model for dichotomous data has a close conceptual relationship to the law of comparative judgment
Law of comparative judgment
The law of comparative judgment was conceived by L. L. Thurstone. In modern day terminology, it is more aptly described as a model that is used to obtain measurements from any process of pairwise comparison...
(LCJ), a model formulated and used extensively by L. L. Thurstone (cf Andrich, 1978b), and therefore also to the Thurstone scale
Thurstone scale
In psychology, the Thurstone scale was the first formal technique for measuring an attitude. It was developed by Louis Leon Thurstone in 1928, as a means of measuring attitudes towards religion. It is made up of statements about a particular issue, and each statement has a numerical value...
.
Prior to introducing the measurement model he is best known for, Rasch had applied the Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
to reading data as a measurement model, hypothesizing that in the relevant empirical context, the number of errors made by a given individual was governed by the ratio of the text difficulty to the person's reading ability. Rasch referred to this model as the multiplicative Poisson model. Rasch's model for dichotomous data – i.e. where responses are classifiable into two categories – is his most widely known and used model, and is the main focus here. This model has the form of a simple logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
.
The brief outline above highlights certain distinctive and interrelated features of Rasch's perspective on social measurement, which are as follows:
- He was concerned principally with the measurement of individuals, rather than with distributions among populations.
- He was concerned with establishing a basis for meeting a priori requirements for measurement deduced from physics and, consequently, did not invoke any assumptions about the distribution of levels of a trait in a population.
- Rasch's approach explicitly recognizes that it is a scientific hypothesis that a given trait is both quantitative and measurable, as operationalized in a particular experimental context.
Thus, congruent with the perspective articulated by Thomas Kuhn
Thomas Kuhn
Thomas Samuel Kuhn was an American historian and philosopher of science whose controversial 1962 book The Structure of Scientific Revolutions was deeply influential in both academic and popular circles, introducing the term "paradigm shift," which has since become an English-language staple.Kuhn...
in his 1961 paper The function of measurement in modern physical science, measurement was regarded both as being founded in theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
, and as being instrumental to detecting quantitative anomalies incongruent with hypotheses related to a broader theoretical framework. This perspective is in contrast to that generally prevailing in the social sciences, in which data such as test scores are directly treated as measurements without requiring a theoretical foundation for measurement. Although this contrast exists, Rasch's perspective is actually complementary to the use of statistical analysis or modelling that requires interval-level measurements, because the purpose of applying the Rasch model is to obtain such measurements. Applications of the Rasch model are described in Sivakumar, Durtis & Hungi (2005).
Invariant comparison and sufficiency
The Rasch model for dichotomous data is often regarded as an item response theoryItem response theory
In psychometrics, item response theory also known as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is based...
(IRT) model with one item parameter. However, rather than being a particular IRT model, proponents of the model regard it as a model that possesses a property which distinguishes it from other IRT models. Specifically, the defining property of Rasch models is their formal or mathematical embodiment of the principle of invariant comparison
Comparison
Comparison may refer to:-Language:* Comparison , a feature of many languages* Degree of comparison, an English language grammatical feature* Mass comparison, a test for the relatedness of languages-Mathematics:...
. Rasch summarised the principle of invariant comparison as follows:
- The comparison between two stimuli should be independent of which particular individuals were instrumental for the comparison; and it should also be independent of which other stimuli within the considered class were or might also have been compared.
- Symmetrically, a comparison between two individuals should be independent of which particular stimuli within the class considered were instrumental for the comparison; and it should also be independent of which other individuals were also compared, on the same or some other occasion (Rasch, 1961, p. 332).
Rasch models embody this principle because their formal structure permits algebraic separation of the person and item parameters, in the sense that the person parameter can be eliminated during the process of statistical estimation of item parameters. This result is achieved through the use of conditional maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimation, in which the response space is partitioned according to person total scores. The consequence is that the raw score for an item or person is the sufficient statistic for the item or person parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
. That is to say, the person total score contains all information available within the specified context about the individual, and the item total score contains all information with respect to item, with regard to the relevant latent trait. The Rasch model requires a specific structure in the response data, namely a probabilistic Guttman
Guttman scale
In statistical surveys conducted by means of structured interviews or questionnaires, a subset of the survey items having binary answers forms a Guttman scale if they can be ranked in some order so that, for a rational respondent, the response pattern can be captured by a single index on that...
structure.
In somewhat more familiar terms, Rasch models provide a basis and justification for obtaining person locations on a continuum from total scores on assessments. Although it is not uncommon to treat total scores directly as measurements, they are actually counts of discrete observations rather than measurements. Each observation represents the observable outcome of a comparison
Comparison
Comparison may refer to:-Language:* Comparison , a feature of many languages* Degree of comparison, an English language grammatical feature* Mass comparison, a test for the relatedness of languages-Mathematics:...
between a person and item. Such outcomes are directly analogous to the observation of the rotation of a balance scale in one direction or another. This observation would indicate that one or other object has a greater mass, but counts of such observations cannot be treated directly as measurements.
Rasch pointed out that the principle of invariant comparison is characteristic of measurement in physics using, by way of example, a two-way experimental frame of reference in which each instrument exerts a mechanical
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
upon solid bodies to produce acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
. Rasch (1960/1980, pp. 112–3) stated of this context: "Generally: If for any two objects we find a certain ratio of their accelerations produced by one instrument, then the same ratio will be found for any other of the instruments". It is readily shown that Newton's second law entails that such ratios are inversely proportional to the ratios of the masses
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the bodies.
The mathematical form of the Rasch model for dichotomous data
Let be a dichotomous random variable where, for example, denotes a correct response and an incorrect response to a given assessment item. In the Rasch model for dichotomous data, the probability of the outcome is given by:where
is the ability of person and is the difficulty of item . Thus, in the case of a dichotomous attainment item, is the probability of success upon interaction between the relevant person and assessment item. It is readily shown that the log oddsOdds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
, or logit
Logit
The logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
, of correct response by a person to an item, based on the model, is equal to
. It can be shown that the log odds of a correct response by a person to one item, conditional on a correct response to one of two items, is equal to the difference between the item locations. For example,where
is the total score of person n over the two items, which implies a correct response to one or other of the items. Hence, the conditional log odds does not involve the person parameter , which can therefore be eliminated by conditioning on the total score . That is, by partitioning the responses according to raw scores and calculating the log odds of a correct response, an estimate is obtained without involvement of . More generally, a number of item parameters can be estimated iteratively through application of a process such as Conditional Maximum Likelihood estimation (see Rasch model estimationRasch model estimation
Estimation of a Rasch model is used to estimate the parameters of the Rasch model. Various techniques are employed to estimate the parameters from matrices of response data. The most common approaches are types of maximum likelihood estimation, such as joint and conditional maximum likelihood...
). While more involved, the same fundamental principle applies in such estimations.
for items with different locations on the latent continuum. The location of an item is, by definition, that location at which the probability that is equal to 0.5. In figure 4, the black circles represent the actual or observed proportions of persons within Class Intervals for which the outcome was observed. For example, in the case of an assessment item used in the context of educational psychologyEducational psychology
Educational psychology is the study of how humans learn in educational settings, the effectiveness of educational interventions, the psychology of teaching, and the social psychology of schools as organizations. Educational psychology is concerned with how students learn and develop, often focusing...
, these could represent the proportions of persons who answered the item correctly. Persons are ordered by the estimates of their locations on the latent continuum and classified into Class Intervals on this basis in order to graphically inspect the accordance of observations with the model. There is a close conformity of the data with the model. In addition to graphical inspection of data, a range of statistical tests of fit are used to evaluate whether departures of observations from the model can be attributed to random effects alone, as required, or whether there are systematic departures from the model.
The polytomous form of the Rasch model
The polytomous Rasch model, which is a generalisation of the dichotomous model, can be applied in contexts in which successive integer scores represent categories of increasing level or magnitude of a latent trait, such as increasing ability, motor function, endorsement of a statement, and so forth. The Polytomous response model is, for example, applicable to the use of Likert scales, grading in educational assessment, and scoring of performances by judges.Other considerations
A criticism of the Rasch model is that it is overly restrictive or prescriptive because it does not permit each item to have a different discrimination. A criticism specific to the use of multiple choice items in educational assessment is that there is no provision in the model for guessing because the left asymptote always approaches a zero probability in the Rasch model. These variations are available in models such as the two and three parameter logistic models (Birnbaum, 1968). However, the specification of uniform discrimination and zero left asymptote are necessary properties of the model in order to sustain sufficiency of the simple, unweighted raw score.In the two-parameter logistic model (2PL-IRT; Lord & Novick, 1968) the weighted raw score is theoretically sufficient for person parameters, where the weights are given by model parameters referred to as discrimination parameters. Lord & Novick's one-parameter logistic model, 1PL, appears similar to the Rasch model in that it does not have discrimination parameters, but 1PL has different motivation and subtly different parameterization. The 1PL is a descriptive model which summarizes the sample as a normal distribution. The dichotomous Rasch model is a measurement model which parameterizes each member of the sample individually. There are other technical differences.
Verhelst & Glas (1995) derive Conditional Maximum Likelihood (CML) equations for a model they refer to as the One Parameter Logistic Model (OPLM). In algebraic form it appears to be identical with the 2PL model, but OPLM contains preset discrimination indexes rather than 2PL's estimated discrimination parameters. As noted by these authors, though, the problem one faces in estimation with estimated discrimination parameters is that the discriminations are unknown, meaning that the weighted raw score "is not a mere statistic, and hence it is impossible to use CML as an estimation method" (Verhelst & Glas, 1995, p. 217). That is, sufficiency of the weighted "score" in the 2PL cannot be used according to the way in which a sufficient statistic is defined. If the weights are imputed instead of being estimated, as in OPLM, conditional estimation is possible and the properties of the Rasch model are retained (Verhelst, Glas & Verstralen, 1995; Verhelst & Glas, 1995). In OPLM, the values of the discrimination index are restricted to between 1 and 15. A limitation of this approach is that in practice, values of discrimination indexes must be preset as a starting point. This means some type of estimation of discrimination is involved when the purpose is to avoid doing so.
The Rasch model for dichotomous data inherently entails a single discrimination parameter which, as noted by Rasch (1960/1980, p. 121), constitutes an arbitrary choice of the unit
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
in terms of which magnitudes of the latent trait are expressed or estimated. However, the Rasch model requires that the discrimination is uniform across interactions between persons and items within a specified frame of reference (i.e. the assessment context given conditions for assessment).
External links
- Institute for Objective Measurement Online Rasch Resources
- Pearson Psychometrics Laboratory, with information about Rasch models
- Journal of Applied Measurement
- Berkeley Evaluation & Assessment Research Center (ConstructMap software)
- Directory of Rasch Software – freeware and paid
- IRT Modeling Lab at U. Illinois Urbana Champ.
- National Council on Measurement in Education (NCME)
- Rasch analysis
- Rasch Measurement Transactions
- The Standards for Educational and Psychological Testing