
Rayleigh number
Encyclopedia
In fluid mechanics
, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow (also known as free convection or natural convection). When the Rayleigh number is below the critical value for that fluid, heat transfer is primarily in the form of conduction
; when it exceeds the critical value, heat transfer is primarily in the form of convection
.
The Rayleigh number is named after Lord Rayleigh
and is defined as the product of the Grashof number, which describes the relationship between buoyancy
and viscosity
within a fluid, and the Prandtl number, which describes the relationship between momentum diffusivity and thermal diffusivity. Hence the Rayleigh number itself may also be viewed as the ratio of buoyancy and viscosity forces times the ratio of momentum and thermal diffusivities.
For free convection near a vertical wall, this number is
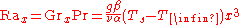
where
In the above, the fluid properties Pr, ν, α and β are evaluated at the film temperature
, which is defined as
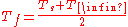
For most engineering purposes, the Rayleigh number is large, somewhere around 106 and 108.
In geophysics
the Rayleigh number is of fundamental importance: it indicates the presence and strength of convection within a fluid body such as the Earth's mantle. The mantle is a solid that behaves as a fluid over geological time scales. The Rayleigh number for the Earth's mantle, due to internal heating alone, RaH is given by

where H is the rate of radiogenic heat production, k is the thermal conductivity
, and D is the depth of the mantle
.
A Rayleigh number for bottom heating of the mantle from the core, RaT can also be defined:

Where ΔTsa is the superadiabatic temperature difference between the reference mantle temperature and the Core–mantle boundary
and c is the specific heat capacity, which is a function of both pressure and temperature.
High values for the Earth's mantle indicates that convection within the Earth is vigorous and time-varying, and that convection is responsible for almost all the heat transported from the deep interior to the surface.
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow (also known as free convection or natural convection). When the Rayleigh number is below the critical value for that fluid, heat transfer is primarily in the form of conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
; when it exceeds the critical value, heat transfer is primarily in the form of convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
.
The Rayleigh number is named after Lord Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
and is defined as the product of the Grashof number, which describes the relationship between buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
within a fluid, and the Prandtl number, which describes the relationship between momentum diffusivity and thermal diffusivity. Hence the Rayleigh number itself may also be viewed as the ratio of buoyancy and viscosity forces times the ratio of momentum and thermal diffusivities.
For free convection near a vertical wall, this number is
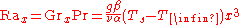
where
- x = Characteristic length (in this case, the distance from the leading edge)
- Rax = Rayleigh number at position x
- Grx = Grashof number at position x
- Pr = Prandtl number
- g = acceleration due to gravity
- Ts = Surface temperature (temperature of the wall)
- T∞ = Quiescent temperature (fluid temperature far from the surface of the object)
- ν = Kinematic viscosity
- α = Thermal diffusivityThermal diffusivityIn heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
- β = Thermal expansion coefficient
In the above, the fluid properties Pr, ν, α and β are evaluated at the film temperature
Film Temperature
In heat transfer and fluid dynamics, the film temperature is an approximation to the temperature of a fluid inside a convection boundary layer...
, which is defined as
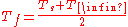
For most engineering purposes, the Rayleigh number is large, somewhere around 106 and 108.
In geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
the Rayleigh number is of fundamental importance: it indicates the presence and strength of convection within a fluid body such as the Earth's mantle. The mantle is a solid that behaves as a fluid over geological time scales. The Rayleigh number for the Earth's mantle, due to internal heating alone, RaH is given by

where H is the rate of radiogenic heat production, k is the thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
, and D is the depth of the mantle
Mantle (geology)
The mantle is a part of a terrestrial planet or other rocky body large enough to have differentiation by density. The interior of the Earth, similar to the other terrestrial planets, is chemically divided into layers. The mantle is a highly viscous layer between the crust and the outer core....
.
A Rayleigh number for bottom heating of the mantle from the core, RaT can also be defined:

Where ΔTsa is the superadiabatic temperature difference between the reference mantle temperature and the Core–mantle boundary
Core–mantle boundary
The core–mantle boundary lies between the Earth's silicate mantle and its liquid iron-nickel outer core. This boundary is located at approximately 2900 km of depth beneath the Earth's surface. The boundary is observed via the discontinuity in seismic wave velocities at that depth...
and c is the specific heat capacity, which is a function of both pressure and temperature.
High values for the Earth's mantle indicates that convection within the Earth is vigorous and time-varying, and that convection is responsible for almost all the heat transported from the deep interior to the surface.
See also
- Grashof number
- Prandtl number
- Reynolds number
- Péclet numberPéclet numberThe Péclet number is a dimensionless number relevant in the study of transport phenomena in fluid flows. It is named after the French physicist Jean Claude Eugène Péclet. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same...
- Nusselt numberNusselt numberIn heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number...

