Rayleigh–Bénard convection
Encyclopedia
Rayleigh–Bénard convection is a type of natural convection
, occurring in a plane of fluid heated from below, in which the fluid develops a regular pattern of convection cells known as Bénard cells. Rayleigh–Bénard convection is one of the most commonly studied convection phenomena because of its analytical and experimental accessibility. The convection patterns are the most carefully examined example of self-organizing nonlinear systems.
Buoyancy
, and hence gravity, is responsible for the appearance of convection cells. The initial movement is the upwelling of warmer liquid from the heated bottom layer. This upwelling spontaneously organizes into a regular pattern of cells.
, a French physicist, in 1900.
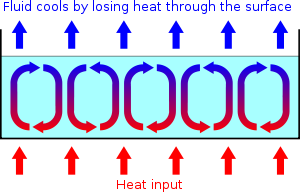The experimental set-up uses a layer of liquid, e.g. water, between two parallel planes. The height of the layer is small compared to the horizontal dimension. At first, the temperature of the bottom plane is the same as the top plane. The liquid will then tend towards an equilibrium
, where its temperature is the same as its surroundings. (Once there, the liquid is perfectly uniform: to an observer it would appear the same from any position. This equilibrium is also asymptotically stable
: after a local, temporary perturbation of the outside temperature, it will go back to its uniform state, in line with the second law of thermodynamics
).
Then, the temperature of the bottom plane is increased slightly yielding a flow of thermal energy conducted through the liquid. The system will begin to have a structure of thermal conductivity
: the temperature, and the density and pressure with it, will vary linearly between the bottom and top plane. A uniform linear gradient of temperature will be established. (This system may be modelled by statistical mechanics
).
Once conduction is established, the microscopic random movement spontaneously becomes ordered on a macroscopic level, forming Bénard convection cells, with a characteristic correlation length.
. Bénard cells are metastable
. This means that a small perturbation will not be able to change the rotation of the cells, but a larger one could affect the rotation; they exhibit a form of hysteresis
.
Moreover, the deterministic law at the microscopic level produces a non-deterministic arrangement of the cells: if the experiment is repeated, a particular position in the experiment will be in a clockwise cell in some cases, and a counter-clockwise cell in others. Microscopic perturbations of the initial conditions are enough to produce a (non-deterministic) macroscopic effect. This inability to predict long-range conditions and sensitivity to initial-conditions are characteristics of chaotic or complex systems (i.e., the butterfly effect
).
If the temperature of the bottom plane was to be further increased, the structure would become more complex in space and time; the turbulent flow would become chaotic
.
Convective Bénard cells tend to approximate regular right hexagonal prisms, particularly in the absence of turbulence, although certain experimental conditions can result in the formation of regular right square prisms or spirals.
. The Rayleigh Number is defined as:
where
As the Rayleigh number increases, the gravitational forces become more dominant. At a critical Rayleigh number of 1708, the instability sets in, and convection cells appear.
The critical Rayleigh number can be obtained analytically for a number of different boundary conditions by doing a perturbation analysis on the linearized equations in the stable state. The simplest case is that of two free boundaries, which Lord Rayleigh solved in 1916. and obtained Rc = π4 ≈ 657.51. In the case of a rigid boundary at the bottom, and a free boundary at the top (which is the situation in an kettle without a lid), the critical Rayleigh number comes out as Rc = 1,100.65.
effects will also play a role in how the convection patterns develop. Liquids flow from places of lower surface tension to places of higher surface tension. This is called the Marangoni effect
. When applying heat from below, the temperature at the top layer will show temperature fluctuations. With increasing temperature, surface tension decreases. Thus a lateral flow of liquid at the surface will take place, from warmer areas to cooler areas. In order to preserve a horizontal (or nearly horizontal) liquid surface, cooler surface liquid will descend. This down-welling of cooler liquid contributes to the driving force of the convection cells. The specific case of temperature gradient-driven surface tension variations is known as thermo-capillary convection, or Bénard–Marangoni convection.
Rayleigh–Bénard convection is also sometimes known as "Bénard–Rayleigh convection", "Bénard convection", or "Rayleigh convection".
Natural convection
Natural convection is a mechanism, or type of heat transport, in which the fluid motion is not generated by any external source but only by density differences in the fluid occurring due to temperature gradients. In natural convection, fluid surrounding a heat source receives heat, becomes less...
, occurring in a plane of fluid heated from below, in which the fluid develops a regular pattern of convection cells known as Bénard cells. Rayleigh–Bénard convection is one of the most commonly studied convection phenomena because of its analytical and experimental accessibility. The convection patterns are the most carefully examined example of self-organizing nonlinear systems.
Buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
, and hence gravity, is responsible for the appearance of convection cells. The initial movement is the upwelling of warmer liquid from the heated bottom layer. This upwelling spontaneously organizes into a regular pattern of cells.
Physical processes
The features of Rayleigh–Bénard convection can be obtained by a simple experiment first conducted by Henri BénardHenri Bénard
Henri Bénard, , French physicist, best known for his research on convection in liquids that now carries his name, Benard convection....
, a French physicist, in 1900.
Development of convection
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, where its temperature is the same as its surroundings. (Once there, the liquid is perfectly uniform: to an observer it would appear the same from any position. This equilibrium is also asymptotically stable
Asymptotic stability
In control theory, a continuous linear time-invariant system is exponentially stable if and only if the system has eigenvalues with strictly negative real parts....
: after a local, temporary perturbation of the outside temperature, it will go back to its uniform state, in line with the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
).
Then, the temperature of the bottom plane is increased slightly yielding a flow of thermal energy conducted through the liquid. The system will begin to have a structure of thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
: the temperature, and the density and pressure with it, will vary linearly between the bottom and top plane. A uniform linear gradient of temperature will be established. (This system may be modelled by statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
).
Once conduction is established, the microscopic random movement spontaneously becomes ordered on a macroscopic level, forming Bénard convection cells, with a characteristic correlation length.
Convection features
The rotation of the cells is stable and will alternate from clock-wise to counter-clockwise horizontally; this is an example of spontaneous symmetry breakingSpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
. Bénard cells are metastable
Metastability
Metastability describes the extended duration of certain equilibria acquired by complex systems when leaving their most stable state after an external action....
. This means that a small perturbation will not be able to change the rotation of the cells, but a larger one could affect the rotation; they exhibit a form of hysteresis
Hysteresis
Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
.
Moreover, the deterministic law at the microscopic level produces a non-deterministic arrangement of the cells: if the experiment is repeated, a particular position in the experiment will be in a clockwise cell in some cases, and a counter-clockwise cell in others. Microscopic perturbations of the initial conditions are enough to produce a (non-deterministic) macroscopic effect. This inability to predict long-range conditions and sensitivity to initial-conditions are characteristics of chaotic or complex systems (i.e., the butterfly effect
Butterfly effect
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
).
If the temperature of the bottom plane was to be further increased, the structure would become more complex in space and time; the turbulent flow would become chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
Convective Bénard cells tend to approximate regular right hexagonal prisms, particularly in the absence of turbulence, although certain experimental conditions can result in the formation of regular right square prisms or spirals.
The Rayleigh–Bénard Instability
Since there is a density gradient between the top and the bottom plate, gravity acts trying to pull the cooler, denser liquid from the top to the bottom. This gravitational force is opposed by the viscous damping force in the fluid. The balance of these two forces is expressed by a non-dimensional parameter called the Rayleigh numberRayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
. The Rayleigh Number is defined as:
where
- Tu is the Temperature of the top plate
- Tb is the Temperature of the bottom plate
- L is the height of the container.
- g is the acceleration due to gravityGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
. - ν is the kinematic viscosity.
- α is the Thermal diffusivityThermal diffusivityIn heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
- β is the Thermal expansion coefficient
As the Rayleigh number increases, the gravitational forces become more dominant. At a critical Rayleigh number of 1708, the instability sets in, and convection cells appear.
The critical Rayleigh number can be obtained analytically for a number of different boundary conditions by doing a perturbation analysis on the linearized equations in the stable state. The simplest case is that of two free boundaries, which Lord Rayleigh solved in 1916. and obtained Rc = π4 ≈ 657.51. In the case of a rigid boundary at the bottom, and a free boundary at the top (which is the situation in an kettle without a lid), the critical Rayleigh number comes out as Rc = 1,100.65.
Effects of surface tension
In case of a free liquid surface in contact with air, buoyancy and surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
effects will also play a role in how the convection patterns develop. Liquids flow from places of lower surface tension to places of higher surface tension. This is called the Marangoni effect
Marangoni effect
The Marangoni effect is the mass transfer along an interface between two fluids due to surface tension gradient...
. When applying heat from below, the temperature at the top layer will show temperature fluctuations. With increasing temperature, surface tension decreases. Thus a lateral flow of liquid at the surface will take place, from warmer areas to cooler areas. In order to preserve a horizontal (or nearly horizontal) liquid surface, cooler surface liquid will descend. This down-welling of cooler liquid contributes to the driving force of the convection cells. The specific case of temperature gradient-driven surface tension variations is known as thermo-capillary convection, or Bénard–Marangoni convection.
History and nomenclature
Rayleigh–Bénard convection, whose effects are due solely to a temperature gradient, was observed originally by Rayleigh; Bénard discovered thermo-capillary convection, which involves surface tension. Nonetheless in modern usage "Rayleigh–Bénard convection" refers to the effects due to temperature, whereas "Bénard–Marangoni convection" refers specifically to the effects of surface tension.Rayleigh–Bénard convection is also sometimes known as "Bénard–Rayleigh convection", "Bénard convection", or "Rayleigh convection".