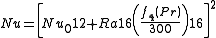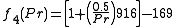Natural convection
Encyclopedia
Natural convection is a mechanism, or type of heat transport, in which the fluid motion is not generated by any external source (like a pump, fan, suction device, etc.) but only by density differences in the fluid occurring due to temperature gradient
s. In natural convection, fluid surrounding a heat source receives heat, becomes less dense and rises. The surrounding, cooler fluid then moves to replace it. This cooler fluid is then heated and the process continues, forming a convection current; this process transfers heat energy from the bottom of the convection cell to top. The driving force for natural convection is buoyancy, a result of differences in fluid density. Because of this, the presence of a proper acceleration
such as arises from resistance to gravity, or an equivalent
force (arising from acceleration
, centrifugal force
or Coriolis force), is essential for natural convection. For example, natural convection essentially does not operate in free-fall (inertial) environments, such as that of the orbiting International Space Station, where other heat transfer mechanisms are required to prevent electronic components from overheating.
Natural convection has attracted a great deal of attention from researchers because of its presence both in nature and engineering applications. In nature, convection cells formed from air raising above sunlight-warmed land or water are a major feature of all weather systems. Convection is also seen in the rising plume of hot air from fire
, oceanic currents, and sea-wind formation (where upward convection is also modified by Coriolis forces). In engineering applications, convection is commonly visualized in the formation of microstructures during the cooling of molten metals, and fluid flows around shrouded heat-dissipation fins, and solar ponds. A very common industrial application of natural convection is free air cooling without the aid of fans: this can happen on small scales (computer chips) to large scale process equipment.
(Ra). This dimensionless number is given by
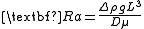
where
is the difference in density between the two parcels of material that are mixing
is the local gravitational acceleration
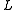is the characteristic length-scale of convection: the depth of the boiling pot, for example
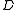is the diffusivity
of the characteristic that is causing the convection, and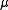
is the dynamic viscosity.
Natural convection will be more likely and/or more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection, and/or a larger distance through the convecting medium. Convection will be less likely and/or less rapid with more rapid diffusion (thereby diffusing away the gradient that is causing the convection) and/or a more viscous (sticky) fluid.
For thermal convection due to heating from below, as described in the boiling pot above, the equation is modified for thermal expansion and thermal diffusivity. Density variations due to thermal expansion are given by:
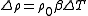
where
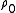is the reference density, typically picked to be the average density of the medium,
is the coefficient of thermal expansion, and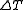
is the temperature difference across the medium.
The general diffusivity,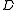
, is redefined as a thermal diffusivity
,
.
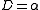
Inserting these substitutions produces a Rayleigh number that can be used to predict thermal convection.
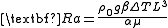
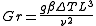
In very sticky, viscous fluids (large ν), fluid movement is restricted, and natural convection will be non-turbulent.
Following the treatment of the previous subsection, the typical fluid velocity is of the order of
, up to a numerical factor depending on the geometry of the system. Therefore Grashof number can be thought of as Reynolds number with the velocity of natural convection replacing the velocity in Reynolds number's formula. However In practice, when referring to the Reynolds number, it is understood that one is considering forced convection, and the velocity is taken as the velocity dictated by external constraints (see below).
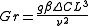
Natural convection is highly dependent on the geometry of the hot surface, various correlations exist in order to determine the heat transfer coefficent.
A general correlation that applies for a variety of geometries is
The value of f4(Pr) is calculated using the following formula
Nu is the Nusselt number
and the values of Nu0 and the characteristic length used to calculate Ra are listed below (see also Discussion):
Warning: The values indicated for the Horizontal Cylinder are wrong, see discussion.
When considering the flow of fluid is a result of heating, the following correlations can be used, assuming the fluid is an ideal diatomic, has adjacent to a vertical plate at constant temperature and the flow of the fluid is completely laminar.
Num = 0.478(Gr0.25)
Mean Nusselt Number = Num = hmL/k
Where
hm = mean coefficient applicable between the lower edge of the plate and any point in a distance L (W/m2. K)
L = height of the vertical surface (m)
k = thermal conductivity (W/m. K)
Grashof Number = Gr =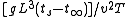
Where
g = gravitational acceleration (m/s2)
L = distance above the lower edge (m)
ts = temperature of the wall (K)
t∞ = fluid temperature outside the thermal boundary layer (K)
v = kinematic viscosity of the fluid (m2/s)
T = absolute temperature (K)
When the flow is turbulent different correlations involving the Rayleigh Number (a function of both the Grashof and the "Prandtl Number" must be used).
Convection, especially Rayleigh-Bénard convection, where the convecting fluid is contained by two rigid horizontal plates, is a convenient example of a pattern forming system
.
When heat is fed into the system from one direction (usually below), at small values it merely diffuses (conducts) from below upward, without causing fluid flow. As the heat flow is increased, above a critical value of the Rayleigh number
, the system undergoes a bifurcation
from the stable conducting state to the convecting state, where bulk motion of the fluid due to heat begins. If fluid parameters other than density do not depend significantly on temperature, the flow profile is symmetric
, with the same volume of fluid rising as falling. This is known as Boussinesq convection.
As the temperature difference between the top and bottom of the fluid becomes higher, significant differences in fluid parameters other than density may develop in the fluid due to temperature. An example of such a parameter is viscosity
, which may begin to significantly vary horizontally across layers of fluid. This breaks the symmetry of the system, and generally changes the pattern of up- and down-moving fluid from stripes to hexagons, as seen at right. Such hexagons are one example of a convection cell
.
As the Rayleigh number
is increased even further above the value where convection cells first appear, the system may undergo other bifurcations, and other more complex patterns, such as spiral
s, may begin to appear.
. Mantle convection is the result of a thermal gradient: the lower mantle is hotter than the upper mantle, and is therefore less dense. This sets up two primary types of instabilities. In the first type, plume
s rise from the lower mantle, and corresponding unstable regions of lithosphere
drip back into the mantle. In the second type, subducting oceanic plates (which largely constitute the upper thermal boundary layer of the mantle) plunge back into the mantle and move downwards towards the core-mantle boundary
. Mantle convection occurs at rates of centimeters per year, and it takes on the order of hundreds of millions of years to complete a cycle of convection.
Neutrino flux measurements from the Earth's core (see kamLAND) show the source of about two-thirds of the heat in the inner core is the radioactive decay
of 40K
, uranium and thorium. This has allowed plate tectonics on Earth to continue far longer than it would have if it were simply driven by heat left over from Earth's formation; or with heat produced from gravitational potential energy
, as a result of physical rearrangement of denser portions of the Earth's interior toward the center of the planet (i.e., a type of prolonged falling and settling).
Temperature gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees per unit length...
s. In natural convection, fluid surrounding a heat source receives heat, becomes less dense and rises. The surrounding, cooler fluid then moves to replace it. This cooler fluid is then heated and the process continues, forming a convection current; this process transfers heat energy from the bottom of the convection cell to top. The driving force for natural convection is buoyancy, a result of differences in fluid density. Because of this, the presence of a proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
such as arises from resistance to gravity, or an equivalent
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
force (arising from acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
or Coriolis force), is essential for natural convection. For example, natural convection essentially does not operate in free-fall (inertial) environments, such as that of the orbiting International Space Station, where other heat transfer mechanisms are required to prevent electronic components from overheating.
Natural convection has attracted a great deal of attention from researchers because of its presence both in nature and engineering applications. In nature, convection cells formed from air raising above sunlight-warmed land or water are a major feature of all weather systems. Convection is also seen in the rising plume of hot air from fire
Fire
Fire is the rapid oxidation of a material in the chemical process of combustion, releasing heat, light, and various reaction products. Slower oxidative processes like rusting or digestion are not included by this definition....
, oceanic currents, and sea-wind formation (where upward convection is also modified by Coriolis forces). In engineering applications, convection is commonly visualized in the formation of microstructures during the cooling of molten metals, and fluid flows around shrouded heat-dissipation fins, and solar ponds. A very common industrial application of natural convection is free air cooling without the aid of fans: this can happen on small scales (computer chips) to large scale process equipment.
Onset
The onset of natural convection is determined by the Rayleigh numberRayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
(Ra). This dimensionless number is given by
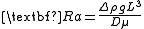
where
is the difference in density between the two parcels of material that are mixing is the local gravitational accelerationGravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
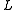is the characteristic length-scale of convection: the depth of the boiling pot, for example 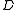is the diffusivityDiffusivity
Diffusivity can refer to:*Diffusivity of heat*Diffusivity of mass:** Molecular diffusivity ** Eddy diffusivity*Momentum diffusivity...
of the characteristic that is causing the convection, and
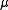is the dynamic viscosity.Natural convection will be more likely and/or more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection, and/or a larger distance through the convecting medium. Convection will be less likely and/or less rapid with more rapid diffusion (thereby diffusing away the gradient that is causing the convection) and/or a more viscous (sticky) fluid.
For thermal convection due to heating from below, as described in the boiling pot above, the equation is modified for thermal expansion and thermal diffusivity. Density variations due to thermal expansion are given by:
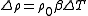
where
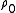is the reference density, typically picked to be the average density of the medium, is the coefficient of thermal expansion, and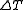 is the temperature difference across the medium.The general diffusivity,
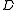, is redefined as a thermal diffusivityThermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
,
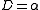
.Inserting these substitutions produces a Rayleigh number that can be used to predict thermal convection.
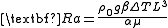
Turbulence
The tendency of a particular naturally convective system towards turbulence relies on the Grashof number (Gr).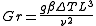In very sticky, viscous fluids (large ν), fluid movement is restricted, and natural convection will be non-turbulent.
Following the treatment of the previous subsection, the typical fluid velocity is of the order of
, up to a numerical factor depending on the geometry of the system. Therefore Grashof number can be thought of as Reynolds number with the velocity of natural convection replacing the velocity in Reynolds number's formula. However In practice, when referring to the Reynolds number, it is understood that one is considering forced convection, and the velocity is taken as the velocity dictated by external constraints (see below).Behavior
The Grashof number can be formulated for natural convection occurring due to a concentration gradient, sometimes termed thermo-solutal convection. In this case, a concentration of hot fluid diffuses into a cold fluid, in much the same way that ink poured into a container of water diffuses to dye the entire space. Then: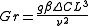Natural convection is highly dependent on the geometry of the hot surface, various correlations exist in order to determine the heat transfer coefficent.
A general correlation that applies for a variety of geometries is
The value of f4(Pr) is calculated using the following formula
Nu is the Nusselt number
Nusselt number
In heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number...
and the values of Nu0 and the characteristic length used to calculate Ra are listed below (see also Discussion):
| Geometry | Characteristic Length | Nu0 |
|---|---|---|
| Inclined Plane | x (Distance along plane) | 0.68 |
| Inclined Disk | 9D/11 (D = Diameter) | 0.56 |
| Vertical Cylinder | x (height of cylinder) | 0.68 |
| Cone | 4x/5 (x = distance along sloping surface) | 0.54 |
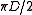| Horizontal Cylinder |  (D = Diameter of cylinder) |
0.36 |
Warning: The values indicated for the Horizontal Cylinder are wrong, see discussion.
Natural Convection from a Vertical Plate
In this system heat is transferred from a vertical plate to a fluid moving parallel to it by natural convection. This will occur in any system wherein the density of the moving fluid varies with position. These phenomena will only be of significance when the moving fluid is minimally affected by forced convection.When considering the flow of fluid is a result of heating, the following correlations can be used, assuming the fluid is an ideal diatomic, has adjacent to a vertical plate at constant temperature and the flow of the fluid is completely laminar.
Num = 0.478(Gr0.25)
Mean Nusselt Number = Num = hmL/k
Where
hm = mean coefficient applicable between the lower edge of the plate and any point in a distance L (W/m2. K)
L = height of the vertical surface (m)
k = thermal conductivity (W/m. K)
Grashof Number = Gr =
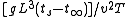
Where
g = gravitational acceleration (m/s2)
L = distance above the lower edge (m)
ts = temperature of the wall (K)
t∞ = fluid temperature outside the thermal boundary layer (K)
v = kinematic viscosity of the fluid (m2/s)
T = absolute temperature (K)
When the flow is turbulent different correlations involving the Rayleigh Number (a function of both the Grashof and the "Prandtl Number" must be used).
Pattern formation
Pattern formation
The science of pattern formation deals with the visible, orderly outcomes of self-organisation and the common principles behind similar patterns....
.
When heat is fed into the system from one direction (usually below), at small values it merely diffuses (conducts) from below upward, without causing fluid flow. As the heat flow is increased, above a critical value of the Rayleigh number
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
, the system undergoes a bifurcation
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
from the stable conducting state to the convecting state, where bulk motion of the fluid due to heat begins. If fluid parameters other than density do not depend significantly on temperature, the flow profile is symmetric
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, with the same volume of fluid rising as falling. This is known as Boussinesq convection.
As the temperature difference between the top and bottom of the fluid becomes higher, significant differences in fluid parameters other than density may develop in the fluid due to temperature. An example of such a parameter is viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, which may begin to significantly vary horizontally across layers of fluid. This breaks the symmetry of the system, and generally changes the pattern of up- and down-moving fluid from stripes to hexagons, as seen at right. Such hexagons are one example of a convection cell
Convection cell
A convection cell is a phenomenon of fluid dynamics that occurs in situations where there are density differences within a body of liquid or gas. The convection usually requires a gravitational field but in microgravity experiments, thermal convection has been observed without gravitational effects...
.
As the Rayleigh number
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
is increased even further above the value where convection cells first appear, the system may undergo other bifurcations, and other more complex patterns, such as spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
s, may begin to appear.
Mantle convection
Convection within Earth's mantle is the driving force for plate tectonicsPlate tectonics
Plate tectonics is a scientific theory that describes the large scale motions of Earth's lithosphere...
. Mantle convection is the result of a thermal gradient: the lower mantle is hotter than the upper mantle, and is therefore less dense. This sets up two primary types of instabilities. In the first type, plume
Plume
Plume may refer to:In science:* Plume , the form of effluent in water or emissions in air* Eruption column, or volcanic plume, a column of hot volcanic ash and gas emitted into the atmosphere during an explosive volcanic eruption...
s rise from the lower mantle, and corresponding unstable regions of lithosphere
Lithosphere
The lithosphere is the rigid outermost shell of a rocky planet. On Earth, it comprises the crust and the portion of the upper mantle that behaves elastically on time scales of thousands of years or greater.- Earth's lithosphere :...
drip back into the mantle. In the second type, subducting oceanic plates (which largely constitute the upper thermal boundary layer of the mantle) plunge back into the mantle and move downwards towards the core-mantle boundary
Core-mantle boundary
The core–mantle boundary lies between the Earth's silicate mantle and its liquid iron-nickel outer core. This boundary is located at approximately 2900 km of depth beneath the Earth's surface. The boundary is observed via the discontinuity in seismic wave velocities at that depth...
. Mantle convection occurs at rates of centimeters per year, and it takes on the order of hundreds of millions of years to complete a cycle of convection.
Neutrino flux measurements from the Earth's core (see kamLAND) show the source of about two-thirds of the heat in the inner core is the radioactive decay
Radioactive decay
Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
of 40K
Potassium
Potassium is the chemical element with the symbol K and atomic number 19. Elemental potassium is a soft silvery-white alkali metal that oxidizes rapidly in air and is very reactive with water, generating sufficient heat to ignite the hydrogen emitted in the reaction.Potassium and sodium are...
, uranium and thorium. This has allowed plate tectonics on Earth to continue far longer than it would have if it were simply driven by heat left over from Earth's formation; or with heat produced from gravitational potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, as a result of physical rearrangement of denser portions of the Earth's interior toward the center of the planet (i.e., a type of prolonged falling and settling).