
Rayleigh–Faber–Krahn inequality
Encyclopedia
In spectral geometry
, the Rayleigh–Faber–Krahn inequality, named after its conjecturer, Lord Rayleigh, and two individuals who independently proved the conjecture, G. Faber and Edgar Krahn
, is an inequality
concerning the lowest Dirichlet eigenvalue
of the Laplace operator
on a bounded domain in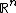 ,
, 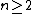 . It states that the first Dirichlet eigenvalue is no less than the corresponding Dirichlet eigenvalue of a Euclidean ball having the same volume. Furthermore, the inequality is rigid in the sense that if the first Dirichlet eigenvalue is equal to that of the corresponding ball, then the domain must actually be a ball.
. It states that the first Dirichlet eigenvalue is no less than the corresponding Dirichlet eigenvalue of a Euclidean ball having the same volume. Furthermore, the inequality is rigid in the sense that if the first Dirichlet eigenvalue is equal to that of the corresponding ball, then the domain must actually be a ball.
More generally, the Faber–Krahn inequality holds in any Riemannian manifold
in which the isoperimetric inequality holds.
Spectral geometry
Spectral geometry is a field in mathematics which concerns relationships between geometric structures of manifolds and spectra of canonically defined differential operators. The case of the Laplace–Beltrami operator on a closed Riemannian manifold has been most intensively studied, although other...
, the Rayleigh–Faber–Krahn inequality, named after its conjecturer, Lord Rayleigh, and two individuals who independently proved the conjecture, G. Faber and Edgar Krahn
Edgar Krahn
Edgar Krahn was an Estonian mathematician.Krahn was born in Sootage, district Laiuse, Estonia, as a member of the Baltic German minority...
, is an inequality
Inequality
In mathematics, an inequality is a statement how the relative size or order of two objects, or about whether they are the same or not .*The notation a b means that a is greater than b....
concerning the lowest Dirichlet eigenvalue
Dirichlet eigenvalue
In mathematics, the Dirichlet eigenvalues are the fundamental modes of vibration of an idealized drum with a given shape. The problem of whether one can hear the shape of a drum is: given the Dirichlet eigenvalues, what features of the shape of the drum can one deduce. Here a "drum" is thought of...
of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
on a bounded domain in
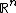 ,
, 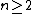 . It states that the first Dirichlet eigenvalue is no less than the corresponding Dirichlet eigenvalue of a Euclidean ball having the same volume. Furthermore, the inequality is rigid in the sense that if the first Dirichlet eigenvalue is equal to that of the corresponding ball, then the domain must actually be a ball.
. It states that the first Dirichlet eigenvalue is no less than the corresponding Dirichlet eigenvalue of a Euclidean ball having the same volume. Furthermore, the inequality is rigid in the sense that if the first Dirichlet eigenvalue is equal to that of the corresponding ball, then the domain must actually be a ball.More generally, the Faber–Krahn inequality holds in any Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
in which the isoperimetric inequality holds.

