
Realizability
Encyclopedia
Realizability is a part of proof theory
which can be used to handle information about formula
s instead of about the proof
s of formulas. A natural number n is said to realize a statement in the language of arithmetic of natural numbers. Other logical and mathematical statements are also realizable, providing a method for interpreting
well formed formulas without resorting to proofs for arriving at those formulas.
introduced the concept of realizability in 1945 in the hopes of it being a faithful mirror of intuitionistic
reasoning, but this conjecture was first disproved by Rose with his example of realizable propositional formula
s that are unprovable in intuitionist calculus. Realizability appears to defy axiomatization due to its complexity
, but it may be approachable through a higher-order Heyting arithmetic
(HA). For HA3, a completeness
property
for the category
of modest sets may be proved from the axiom
s which characterize the realizability of HA3.
as the language of realizers. Modified realizability is one way to show that Markov's principle
is not derivable in intuitionistic logic. On the contrary, it allows to constructively justify the principle of independence of premisses: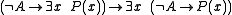 .
.
Relative realizability is an intuitionist analysis of recursive or recursively enumerable elements of data structures that are not necessarily computable, such as computable operations on all real numbers when reals can be only approximated on digital computer systems.
.
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
which can be used to handle information about formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s instead of about the proof
Proof
Proof may refer to:* Proof , sufficient evidence or argument for the truth of a proposition* Formal proof* Mathematical proof, a convincing demonstration that some mathematical statement is necessarily true...
s of formulas. A natural number n is said to realize a statement in the language of arithmetic of natural numbers. Other logical and mathematical statements are also realizable, providing a method for interpreting
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
well formed formulas without resorting to proofs for arriving at those formulas.
Origins
KleeneStephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
introduced the concept of realizability in 1945 in the hopes of it being a faithful mirror of intuitionistic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
reasoning, but this conjecture was first disproved by Rose with his example of realizable propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
s that are unprovable in intuitionist calculus. Realizability appears to defy axiomatization due to its complexity
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
, but it may be approachable through a higher-order Heyting arithmetic
Heyting arithmetic
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
(HA). For HA3, a completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
property
Property (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
for the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of modest sets may be proved from the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s which characterize the realizability of HA3.
Later developments
The modified realizability uses typed lambda calculusTyped lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
as the language of realizers. Modified realizability is one way to show that Markov's principle
Markov's principle
Markov's principle, named after Andrey Markov Jr, is a classical tautology that is not intuitionistically valid but that may be justified by constructive means.There are many equivalent formulations of Markov's principle.- Statements of the principle :...
is not derivable in intuitionistic logic. On the contrary, it allows to constructively justify the principle of independence of premisses:
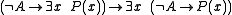 .
.Relative realizability is an intuitionist analysis of recursive or recursively enumerable elements of data structures that are not necessarily computable, such as computable operations on all real numbers when reals can be only approximated on digital computer systems.
Applications in computer science
Modified realizability justifies the process of program extraction implemented in some proof assistants such as CoqCoq
In computer science, Coq is an interactive theorem prover. It allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification...
.
External links
- Realizability Collection of links to recent papers on realizability and related topics.

