Reciprocal polynomial
Encyclopedia
In mathematics
, for a polynomial
p with complex
coefficients,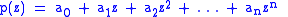
we define the reciprocal polynomial, p*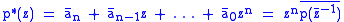
where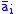
denotes the complex conjugate
of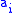
.
A polynomial is called self-reciprocal if
.
If the coefficients ai are real
then this reduces to ai = an−i. In this case p is also called a palindromic polynomial.
If p(z) is the minimal polynomial of z0 with |z0| = 1, and p(z) has real
coefficients, then p(z) is self-reciprocal. This follows because
.
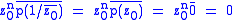So z0 is a root of the polynomial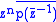
which has degree n. But, the minimal polynomial is unique, hence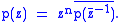
A consequence is that the cyclotomic polynomial
s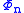
are self-reciprocal for 
; this is used in the special number field sieve
to allow numbers of the form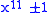
, 
, 
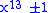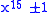and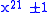 
to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively - note that 
of the exponents are 10, 12, 8 and 12.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, for a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
p with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients,
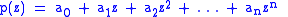
we define the reciprocal polynomial, p*
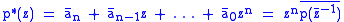
where
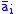denotes the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of
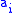.A polynomial is called self-reciprocal if
.If the coefficients ai are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
then this reduces to ai = an−i. In this case p is also called a palindromic polynomial.
If p(z) is the minimal polynomial of z0 with |z0| = 1, and p(z) has real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficients, then p(z) is self-reciprocal. This follows because
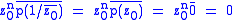.So z0 is a root of the polynomial
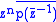which has degree n. But, the minimal polynomial is unique, hence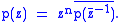A consequence is that the cyclotomic polynomial
Cyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
s
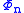are self-reciprocal for ; this is used in the special number field sieveSpecial number field sieve
In number theory, a branch of mathematics, the special number field sieve is a special-purpose integer factorization algorithm. The general number field sieve was derived from it....
to allow numbers of the form
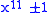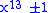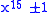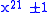, , and to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively - note that of the exponents are 10, 12, 8 and 12.External links
- Reciprocal Polynomial (on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
)