Rectified 10-orthoplex
Encyclopedia
10-orthoplex |
Rectified 10-orthoplex |
Birectified 10-orthoplex |
Trirectified 10-orthoplex |
Quadirectified 10-orthoplex |
Quadrirectified 10-cube |
Trirectified 10-cube |
Birectified 10-cube |
Rectified 10-cube Rectified 10-cube In ten-dimensional geometry, a rectified 10-cube is a convex uniform 10-polytope, being a rectification of the regular 10-cube.There are 10 rectifications of the 10-cube, with the zeroth being the 10-cube itself. Vertices of the rectified 10-cube are located at the edge-centers of the 10-cube... |
10-cube 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... |
||
| Orthogonal projections in A10 Coxeter plane | |||
|---|---|---|---|
In ten-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a rectified 10-orthoplex is a convex uniform 10-polytope, being a rectification
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
of the regular 10-orthoplex.
There are 10 rectifications of the 10-orthoplex. Vertices of the rectified 10-orthoplex are located at the edge-centers of the 9-orthoplex. Vertices of the birectified 10-orthoplex are located in the triangular face centers of the 10-orthoplex. Vertices of the trirectified 10-orthoplex are located in the tetrahedral
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
cell centers of the 10-orthoplex.
These polytopes are part of a family 1023 uniform 10-polytopes with BC10 symmetry.
Rectified 10-orthoplex
| Rectified 10-orthoplex | |
|---|---|
| Type | uniform 10-polytope |
| Schläfli symbol | t1{3,3,3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 2880 |
| Vertices | 180 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
8-orthoplex prism |
| Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
icosagon Icosagon In geometry, an icosagon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.One interior angle in a regular icosagon is 162° meaning that one exterior angle would be 18°... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
C10, [4,38] D10, [37,1,1] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
In ten-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a rectified 10-orthoplex is an 10-polytope
10-polytope
In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets....
, being a rectification
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
of the regular 10-orthoplex.
Rectified 10-orthoplex
The rectified 10-orthoplex is the vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
for the demidekeractic honeycomb.
- or
Construction
There are two Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s associated with the rectified 10-orthoplex, one with the C10 or [4,3,3,3,3,3,3,3,3] Coxeter group, and a lower symmetry with two copies of 9-orthoplex facets, alternating, with the D10 or [37,1,1] Coxeter group.
Cartesian coordinates
Cartesian coordinates for the vertices of a rectified 10-orthoplex, centered at the origin, edge length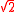
are all permutations of:
- (±1,±1,0,0,0,0,0,0,0,0)
Root vectors
Its 180 vertices represent the root vectors of the simple Lie groupSimple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
D10. When combined with the 20 vertices of the 9-orthoplex, these vertices represent the 200 root vectors of the simple Lie group B10.
Birectified 10-orthoplex
| Birectified 10-orthoplex | |
|---|---|
| Type | uniform 10-polytope |
| Schläfli symbol | t2{3,3,3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
C10, [4,38] D10, [37,1,1] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
Trirectified 10-orthoplex
| Trirectified 10-orthoplex | |
|---|---|
| Type | uniform 10-polytope |
| Schläfli symbol | t3{3,3,3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
C10, [4,38] D10, [37,1,1] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
Quadrirectified 10-orthoplex
| Quadrirectified 10-orthoplex | |
|---|---|
| Type | uniform 10-polytope |
| Schläfli symbol | t4{3,3,3,3,3,3,3,3,4} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| 7-faces | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
C10, [4,38] D10, [37,1,1] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |