
Reduced residue system
Encyclopedia
Any subset R of the set of integers is called a reduced residue system modulo n if
Here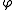 denotes Euler's totient function
denotes Euler's totient function
.
A reduced residue system modulo n can be formed from a complete residue system modulo n by removing all integers not relatively prime to n. For example, a complete residue system modulo 12 is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}. 1, 5, 7 and 11 are the only integers in this set which are relatively prime to 12, and so the corresponding reduced residue system modulo 12 is {1,5,7,11}. Note that the cardinality of this set is . Some other reduced residue systems modulo 12 are
. Some other reduced residue systems modulo 12 are
- gcd(r, n) = 1 for each r contained in R;
- R contains φ(n) elements;
- no two elements of R are congruent modulo n.
Here
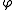 denotes Euler's totient function
denotes Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
A reduced residue system modulo n can be formed from a complete residue system modulo n by removing all integers not relatively prime to n. For example, a complete residue system modulo 12 is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}. 1, 5, 7 and 11 are the only integers in this set which are relatively prime to 12, and so the corresponding reduced residue system modulo 12 is {1,5,7,11}. Note that the cardinality of this set is
 . Some other reduced residue systems modulo 12 are
. Some other reduced residue systems modulo 12 are- {13,17,19,23}
- {−11,−7,−5,−1}
- {−7,−13,13,31}
- {35,43,53,61}
Facts
- If is a reduced residue system with n > 2, then
 .
. - Every number in a reduced residue system mod n (except for 1) is a generator for the multiplicative group of integers mod nMultiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
.
See also
- Complete residue system modulo m
- Congruence relationCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
- Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
- Greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
- Least residue system modulo m
- Modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
- Number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
- Residue number systemResidue number systemA residue number system represents a large integer using a set of smaller integers, so that computation may be performed more efficiently...
External links
- Residue systems at PlanetMath
- Reduced residue system at MathWorld

