Redundant binary representation
Encyclopedia
A redundant binary representation (RBR) is a numeral system
that uses more bits than needed to represent a single binary digit
so that most numbers have several representations. A RBR is unlike usual binary numeral system
s, including two's complement
, which use a single bit for each digit. Many of a RBR's properties differ from those of regular binary representation systems. Most importantly, a RBR allows addition without using a typical carry. When compared to non-redundant representation, a RBR makes bitwise logical operation
slower, but arithmetic operations are faster when a greater bit width is used. Usually, each digit has its own sign that is not necessarily the same as the sign of the number represented. When digits have signs, that RBR is also a signed-digit representation
.
. In a RBR, digit
s are pairs of bits, that is, for every place, a RBR uses a pair of bits. The value represented by an RBR digit can be found using a translation table. This table indicates the mathematical value of each possible pair of bits.
As in conventional binary representation, the integer
value of a given representation is a weighted sum of the values of the digits. The weight starts at 1 for the rightmost position and goes up by a factor of 2 for each next position. Usually, a RBR allows negative values. There is no single sign bit that tells if a RBR represented number is positive or negative. Most integers have several possible representations in an RBR.
An integer
value can be converted back from a RBR using the following formula, where n is the number of digit and dk is the interpreted value of the k-th digit, where k starts at 0 at the rightmost position: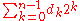
The conversion from a RBR to two's complement can be done in O(log(n)) using prefix adder where n is the number of digit.
Not all RBR have the same properties. For example, using the translation table on the right, the number 1 can be represented in this RBR in many ways: "01·01·01·11", "01·01·10·11", "01·01·11·00", "11·00·00·00". Also, for this translation table, flipping all bits (NOT gate) corresponds to finding the additive inverse
(multiplication
by −1) of the integer represented.
In this case: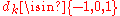
s.
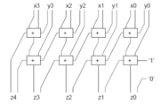
In particular, a carry-save adder uses a RBR.
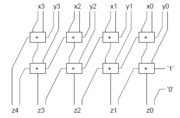The addition operation in all RBRs is carry-free, which means that the carry does not have to propagate through all the width of the addition unit. In effect, the addition in all RBRs is a constant-time operation. The addition will always take the same amount of time independent of the bit width of the operand
s. This does not imply that the addition is always faster in a RBR than is two's complement
representation, but that the addition will eventually be faster in a RBR with increasing bit width because the two's complement addition unit's delay is proportional to log(n) (where n is the bit width). The addition in a RBR take a constant time because each digit of the result can be calculated independently of one another, implying that each digit of the result can be calculated in parallel. A few of the adders can be found here
of the second operand needs to be computed first. The additive inverse
is usually found using a translation table.
operation on a pair of representations of 1 is expected to have value 1 in usual representations. Since there are many ways to represent 1 in a RBR, it is not possible to simply use the basic logic gate AND
between every digit. The same problem apply to the OR
and XOR operations. While it is possible to do bitwise operation
s directly on the underlying bits inside a RBR, it is not clear that this is a meaningful operation. Assuming one wants the result to represent the same integer value as if the operation had been carried out using a standard non-redundant binary representation, it is necessary to convert the two operands first to non-redundant representations. Consequently, logical operations are slower in a RBR. More precisely, they take a time proportional to log(n) (where n is the number of digit) compared to a constant-time in two's complement
.
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
that uses more bits than needed to represent a single binary digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
so that most numbers have several representations. A RBR is unlike usual binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
s, including two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
, which use a single bit for each digit. Many of a RBR's properties differ from those of regular binary representation systems. Most importantly, a RBR allows addition without using a typical carry. When compared to non-redundant representation, a RBR makes bitwise logical operation
Bitwise operation
A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
slower, but arithmetic operations are faster when a greater bit width is used. Usually, each digit has its own sign that is not necessarily the same as the sign of the number represented. When digits have signs, that RBR is also a signed-digit representation
Signed-digit representation
Signed-digit representation of numbers indicates that digits can be prefixed with a − sign to indicate that they are negative.Signed-digit representation can be used in low-level software and hardware to accomplish fast addition of integers because it can eliminate carries...
.
Conversion from RBR
A RBR is a place-value notation systemPositional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
. In a RBR, digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s are pairs of bits, that is, for every place, a RBR uses a pair of bits. The value represented by an RBR digit can be found using a translation table. This table indicates the mathematical value of each possible pair of bits.
As in conventional binary representation, the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
value of a given representation is a weighted sum of the values of the digits. The weight starts at 1 for the rightmost position and goes up by a factor of 2 for each next position. Usually, a RBR allows negative values. There is no single sign bit that tells if a RBR represented number is positive or negative. Most integers have several possible representations in an RBR.
An integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
value can be converted back from a RBR using the following formula, where n is the number of digit and dk is the interpreted value of the k-th digit, where k starts at 0 at the rightmost position:
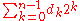
The conversion from a RBR to two's complement can be done in O(log(n)) using prefix adder where n is the number of digit.
Example of redundant binary representation
| Digit | Interpreted value |
|---|---|
| 00 | −1 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
Not all RBR have the same properties. For example, using the translation table on the right, the number 1 can be represented in this RBR in many ways: "01·01·01·11", "01·01·10·11", "01·01·11·00", "11·00·00·00". Also, for this translation table, flipping all bits (NOT gate) corresponds to finding the additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
(multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by −1) of the integer represented.
In this case:
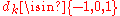
Arithmetic operations
A RBR is used by particular arithmetic logic unitArithmetic logic unit
In computing, an arithmetic logic unit is a digital circuit that performs arithmetic and logical operations.The ALU is a fundamental building block of the central processing unit of a computer, and even the simplest microprocessors contain one for purposes such as maintaining timers...
s.
In particular, a carry-save adder uses a RBR.
Addition
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
s. This does not imply that the addition is always faster in a RBR than is two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
representation, but that the addition will eventually be faster in a RBR with increasing bit width because the two's complement addition unit's delay is proportional to log(n) (where n is the bit width). The addition in a RBR take a constant time because each digit of the result can be calculated independently of one another, implying that each digit of the result can be calculated in parallel. A few of the adders can be found here
Subtraction
Subtraction is the same as the addition except that the additive inverseAdditive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of the second operand needs to be computed first. The additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
is usually found using a translation table.
Logical operations
Implementing logical operations in a RBR using digital logic is more complicated than in usual representations. For example, the expected result of the bitwise ANDAND gate
The AND gate is a basic digital logic gate that implements logical conjunction - it behaves according to the truth table to the right. A HIGH output results only if both the inputs to the AND gate are HIGH . If neither or only one input to the AND gate is HIGH, a LOW output results...
operation on a pair of representations of 1 is expected to have value 1 in usual representations. Since there are many ways to represent 1 in a RBR, it is not possible to simply use the basic logic gate AND
AND gate
The AND gate is a basic digital logic gate that implements logical conjunction - it behaves according to the truth table to the right. A HIGH output results only if both the inputs to the AND gate are HIGH . If neither or only one input to the AND gate is HIGH, a LOW output results...
between every digit. The same problem apply to the OR
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
and XOR operations. While it is possible to do bitwise operation
Bitwise operation
A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
s directly on the underlying bits inside a RBR, it is not clear that this is a meaningful operation. Assuming one wants the result to represent the same integer value as if the operation had been carried out using a standard non-redundant binary representation, it is necessary to convert the two operands first to non-redundant representations. Consequently, logical operations are slower in a RBR. More precisely, they take a time proportional to log(n) (where n is the number of digit) compared to a constant-time in two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
.