Refactorable number
Encyclopedia
A refactorable number or tau number is an integer n that is divisible by the count of its divisor
s, or to put it algebraically, n is such that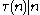
. The first few refactorable numbers are listed in 1, 2, 8, 9, 12
, 18
, 24
, 36
, 40
, 56
, 60
, 72
, 80
, 84
, 88
, 96
. For example, 18 has 6 divisors (1 and 18, 2 and 9, 3 and 6) and is divisible by 6.
Cooper and Kennedy proved that refactorable numbers have natural density
zero. Zelinsky proved that no three consecutive integers can all be refactorable. Colton proved that no refactorable number is perfect
. The equation GCD
(n, x) = τ(n) has solutions only if n is a refactorable number.
There are still unsolved problems regarding refactorable numbers. Colton asked if there are there arbitrarily large n such that both n and n + 1 are refactorable. Zelinsky wondered if there exists a refactorable number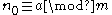
, does there necessarily exist 
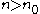such that n is refactorable and 
.
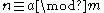and Robert E. Kennedy where they showed that the tau numbers has natural density
zero, they were later rediscovered by Simon Colton
using a computer program he had made which invents and judges definitions from a variety of areas of mathematics such as number theory
and graph theory
. Colton called such numbers "refactorable". While computer programs had discovered proofs before, this discovery was one of the first times that a computer program had discovered a new or previously obscure idea. Colton proved many results about refactorable numbers, showing that there were infinitely many and proving a variety of congruence restrictions on their distribution. Colton was only later alerted that Kennedy and Cooper had previously investigated the topic.
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s, or to put it algebraically, n is such that
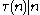. The first few refactorable numbers are listed in 1, 2, 8, 9, 1212 (number)
12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 18
18 (number)
18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress...
, 24
24 (number)
24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
, 36
36 (number)
36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number...
, 40
40 (number)
40 is the natural number following 39 and preceding 41.Despite being related to the word "four" , 40 is spelled "forty", and not "fourty"...
, 56
56 (number)
56 is the natural number following 55 and preceding 57.- Mathematics :56 is the sum of the first six triangular numbers , as well as the sum of six consecutive primes . It is also a tetranacci number and a pronic number. Adding up the divisors of 1 through 8 gives 56...
, 60
60 (number)
60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:...
, 72
72 (number)
72 is the natural number following 71 and preceding 73. It is half a gross or 6 dozen .-In mathematics:...
, 80
80 (number)
80 is the natural number following 79 and preceding 81.- In mathematics :The sum of Euler's totient function φ over the first sixteen integers is 80....
, 84
84 (number)
84 is the natural number following 83 and preceding 85.- In mathematics :Eighty-four is the sum of the first seven triangular numbers , as well as the sum of a twin prime...
, 88
88 (number)
88 is the natural number following 87 and preceding 89.- In mathematics :Eighty-Eight is a refactorable number, a primitive semiperfect number and an untouchable number...
, 96
96 (number)
96 is the natural number following 95 and preceding 97.-In mathematics:Ninety-six is an octagonal number, a refactorable number and an untouchable number. Since it is a multiple of 6, it is a semiperfect number...
. For example, 18 has 6 divisors (1 and 18, 2 and 9, 3 and 6) and is divisible by 6.
Cooper and Kennedy proved that refactorable numbers have natural density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
zero. Zelinsky proved that no three consecutive integers can all be refactorable. Colton proved that no refactorable number is perfect
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
. The equation GCD
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(n, x) = τ(n) has solutions only if n is a refactorable number.
There are still unsolved problems regarding refactorable numbers. Colton asked if there are there arbitrarily large n such that both n and n + 1 are refactorable. Zelinsky wondered if there exists a refactorable number
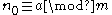, does there necessarily exist 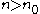such that n is refactorable and 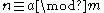.History
First defined by Curtis CooperCurtis Cooper (mathematician)
Curtis Niles Cooper is an American mathematician. He currently is a professor at the University of Central Missouri, in the Department of Mathematics and Computer Science....
and Robert E. Kennedy where they showed that the tau numbers has natural density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
zero, they were later rediscovered by Simon Colton
Simon Colton
Simon Colton is a British computer scientist, currently working in the Computational Creativity Group at Imperial College London, where he holds the position of Reader. He graduated from the University of Durham with a degree in Mathematics, gained a MSc...
using a computer program he had made which invents and judges definitions from a variety of areas of mathematics such as number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. Colton called such numbers "refactorable". While computer programs had discovered proofs before, this discovery was one of the first times that a computer program had discovered a new or previously obscure idea. Colton proved many results about refactorable numbers, showing that there were infinitely many and proving a variety of congruence restrictions on their distribution. Colton was only later alerted that Kennedy and Cooper had previously investigated the topic.