For reflection principles in set theory, see reflection principle

Reflection principle

In set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...

.

In algebraic number theory

Algebraic number theory

Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...

, a reflection theorem or Spiegelungssatz (German

German language

German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....

 for reflection theorem – see Spiegel

Spiegel

Spiegel is German, Yiddish, and Dutch for "mirror". More specifically, it may refer to:* Der Spiegel , the weekly German magazine** Spiegel scandal, a 1962 German political scandal, named after the Der Spiegel magazine...

and Satz

Satz (disambiguation)

Satz is a German word and name, and may refer to:* Satz, a formal section in music analysis* "theorem" in German, conventionally used in the name of certain theorems. Note however that the word "Theorem" is also used in German, generally for more important results, and thus in a stricter...

) is one of a collection of theorems linking the sizes of different ideal class group

Ideal class group

In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...

s (or ray class groups), or the sizes of different isotypic component

Isotypic component

The Isotypic component of weight \lambda of a Lie algebra module is the sum of all submodules which are isomorphic to the highest weight module with weight \lambda.-Definition:...

s of a class group. The original example is due to Ernst Eduard Kummer

Ernst Kummer

Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...

, who showed that the class number of the cyclotomic field

Cyclotomic field

In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...

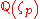 , with p a prime number, will be divisible by p if the class number of the maximal real subfield 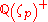is. Another example is due to Scholz. A simplified version of his theorem states that if 3 divides the class number of a real quadratic field , then 3 also divides the class number of the imaginary quadratic field .

Both of the above results are generalized by Leopoldt's "Spiegelungssatz", which relates the p-ranks of different isotypic components of the class group of a number field K, considered as a module

Galois module

In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...

 over the Galois group

Galois group

In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...

 of a Galois extension K/k. Extensions of his Spiegelungssatz were given by Oriat and Oriat-Satge, where class groups were no longer associated with characters of the Galois group of K/k, but rather by ideals in a group ring

Group ring

In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...

 over the Galois group of K/k. Leopoldt's Spiegelungssatz was generalized in a different direction by Kuroda, who extended it to a statement about ray class groups. This was further developed into the very general "T-S reflection theorem" of Georges Gras. Kenkichi Iwasawa

Kenkichi Iwasawa

Kenkichi Iwasawa was a Japanese mathematician who is known for his influence on algebraic number theory.Iwasawa was born in Shinshuku-mura, a town near Kiryū, in Gunma Prefecture...

 also provided an Iwasawa-theoretic

Iwasawa theory

In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...

reflection theorem.