Reflections of signals on conducting lines
Encyclopedia
A signal travelling along an electrical transmission line
will be partly, or wholly, reflected
back in the opposite direction when the travelling signal encounters a discontinuity in the transmission parameters of the line, or at the far end of the line if the line is not correctly terminated
in its characteristic impedance
. This can happen, for instance, if two lengths of dissimilar transmission lines are joined together.
This article is about signal reflection
s on electrically conducting lines. Such lines are loosely referred to as copper
lines, and indeed, in telecommunications are generally made from copper, but other metals are used, notably aluminium
in power lines. Although this article is limited to describing reflections on conducting lines, this is essentially the same phenomenon as optical reflections in fibre-optic lines and microwave
reflections in waveguide
s.
Reflections cause several undesirable effects, including modifying frequency response
s, causing overload
power in transmitter
s and overvoltage
s on power line
s. However, the reflection phenomenon can also be made use of in such devices as stubs and impedance transformers
.
s is particularly enlightening. A simple example is a step voltage,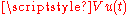
, applied to one end of a lossless line, and consider what happens when the line is terminated in various ways. The step will be propagated down the line according to the telegrapher's equation at some velocity 
and the incident voltage at some point 
on the line is given by
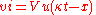
The incident current in the line is given by the characteristic impedance
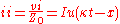
the step will arrive at the open circuit at time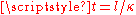 
, at which point the current in the line is zero (by the definition of an open circuit). Since charge continues to arrive at the end of the line through the incident current, but no current is leaving the line, then conservation of electric charge requires that there must be an equal and opposite current into the end of the line. Essentially, this is Kirchhoff's current law
in operation. This equal and opposite current is the reflected current,
, and since
there must also be a reflected voltage,
, to drive the reflected current down the line. This reflected voltage must exist by reason of conservation of energy. The source is supplying energy to the line at a rate of 
. None of this energy is dissipated in the line or its termination and it must go somewhere. The only available direction is back up the line. Since the reflected current is equal in magnitude to the incident current, it must also be so that
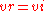
These two voltages will add to each other so that after the step has been reflected, twice the incident voltage appears across the output terminals of the line. As the reflection proceeds back up the line the reflected voltage continues to add to the incident voltage and the reflected current continues to subtract from the incident current. After a further interval of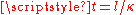
the reflected step arrives at the generator end and the condition of double voltage and zero current will pertain there also as well as all along the length of the line. If the generator is matched to the line with an impedance of 
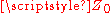the step transient will be absorbed in the generator internal impedance and there will be no further reflections.
This doubling of voltage is a problem frequently arising when switching operations are carried out on power grids. A brief open circuit while switching is in progress will cause such a reflection and a voltage "spike" results. This counter-intuitive result may become clearer if the circuit voltages are considered when the line is so short that it can be ignored for the purposes of analysis. The equivalent circuit of a generator matched to a load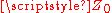
to which it is delivering a voltage 
can be represented as in figure 2. That is, the generator can be represented as an ideal voltage generator of twice the voltage it is to deliver and an internal impedance of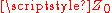 
.
However if the generator is left open circuit, a voltage of
appears at the generator output terminals as in figure 3. The same situation pertains if a very short transmission line is inserted between the generator and the open circuit. If, however, a longer line with a characteristic impedance of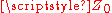 
and noticeable end-to-end delay is inserted, the generator – being initially matched to the impedance of the line – will have 
at the output. But after an interval, a reflected transient will return from the end of the line with the "information" on what the line is actually terminated with, and the voltage will become 
as before.
:
and,
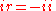
As the reflection travels back up the line, the two voltages subtract and cancel, while the currents will add (the reflection is double negative - a negative current travelling in the reverse direction), the dual situation to the open circuit case.
travelling down the line and analyse it in the frequency domain
. The impedance is consequently represented as a frequency
dependant complex function.
For a line terminated in its own characteristic impedance there is no reflection. By definition, terminating in the characteristic impedance has the same effect as an infinitely long line. Any other impedance will result in a reflection. The magnitude of the reflection will be smaller than the magnitude of the incident wave if the terminating impedance is wholly or partly resistive since some of the energy of the incident wave will be absorbed in the resistance. The voltage across the terminating impedance may be calculated by replacing the output of the line with an equivalent generator (figure 4) and is given by
The reflection,
must be the exact amount required to make 
,
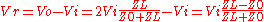
The reflection coefficient is defined as
and substituting in the expression for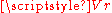
,
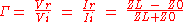
In general
is a complex function but the above expression shows that the magnitude is limited to
when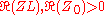 
The physical interpretation of this is that the reflection cannot be greater than the incident wave when only passive elements are involved (but see negative resistance amplifier for an example where this condition does not hold). For the special cases described above,
When both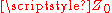
and 
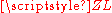are purely resistive then 
must be purely real. In the general case when 
is complex, this is to be interpreted as a shift in phase
of the reflected wave relative to the incident wave.
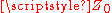is purely real and 
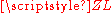is purely imaginary, 
, that is, it is a reactance
. In this case,
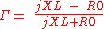
Since
then
showing that all the incident wave is reflected, and none of it is absorbed in the termination, as is to be expected from a pure reactance. There is, however, a change of phase in the reflection given by
In a similar manner, a transmission coefficient can be defined to describe the portion of the wave that it is transmitted in the forward direction:
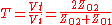
Another kind of discontinuity is caused when both sections of line have an identical characteristic impedance but there is a lumped element at the discontinuity. For the example shown (figure 6) of a shunt lumped element,
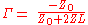
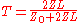
Similar expressions can be developed for a series element, or any electrical network for that matter.
of the two waves will add. There will be other points where the two waves are in anti-phase and will consequently subtract. At these latter points the amplitude is at a minimum and they are known as nodes
. If the incident wave has been totally reflected and the line is lossless, there will be complete cancellation at the nodes with zero signal present there despite the ongoing transmission of waves in both directions. The points where the waves are in phase are anti-nodes and represent a peak in amplitude. Nodes and anti-nodes alternate along the line and the combined wave amplitude varies continuously between them. The combined (incident plus reflected) wave appears to be standing still on the line and is called a standing wave
.
The incident wave can be characterised in terms of the line's propagation constant
,
, source voltage, 
and distance from the source, , by
However, it is often more convenient to work in terms of distance from the load () and the incident voltage that has arrived there (
).
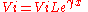
The exponent is positive because
is measured in the reverse direction back up the line and the voltage is increasing closer to the source. Likewise the reflected voltage is given by
The total voltage on the line is given by
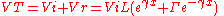
It is often convenient to express this in terms of hyperbolic function
s
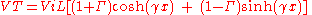
Similarly, the total current on the line is
The voltage nodes (current nodes are not at the same locations) and anti-nodes occur when
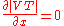
This does not have an easy analytical solution in the general case, but in the case of lossless lines (or lines that are short enough to be considered so)
can be replaced by 
where 
is the phase change constant. The voltage equation then reduces to trigonometric functions
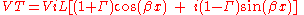
and the partial differential of the magnitude of this yields the condition,
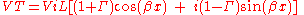
Expressing
in terms of wavelength, 
, allows 
to be solved in terms of 
:
is purely real when the termination is short circuit or open circuit, or when both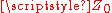 
and 
are purely resistive. In those cases the nodes and anti-nodes are given by
which solves for
at
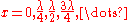
For
the first point is a node, for 
the first point is an anti-node and thenceforth they will alternate. For terminations that are not purely resistive the spacing and alternation remain the same but the whole pattern is shifted along the line by a constant amount related to the phase of 
.
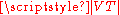at anti-nodes and nodes is called the voltage standing wave ratio (VSWR) and is related to the reflection coefficient by
for a lossless line. For a lossy line the expression is only valid adjacent to the termination; VSWR asymptotically
approaches unity with distance from the termination or discontinuity.
VSWR and the positions of the nodes are parameters that can be directly measured with an instrument called a slotted line. This instrument makes use of the reflection phenomenon to make many different measurements at microwave frequencies. One use is that VSWR and node position can be used to calculate the impedance of a test component terminating the slotted line. This is a useful method because measuring impedances by directly measuring voltages and currents is difficult at these frequencies.
and will be a function of the length of the line. The value of this impedance can be found by dividing the expression for total voltage by the expression for total current given above:
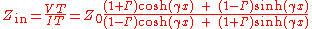
Substituting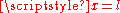
, the length of the line and dividing through by 
reduces this to
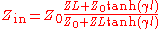
As before, when considering just short pieces of transmission line,
can be replaced by 
and the expression reduces to trigonometric functions
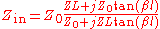
By suitable choice of length, the stub can be used in place of a capacitor, an inductor or a resonant circuit.
The other structure is the quarter wave impedance transformer
. As its name suggests, this is a line exactly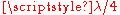
in length. Since 
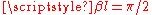this will produce the inverse of its terminating impedance
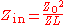
Both of these structures are widely used in distributed element filter
s and impedance matching
networks.
Transmission line
In communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that its wave nature must be taken into account...
will be partly, or wholly, reflected
Reflection (physics)
Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...
back in the opposite direction when the travelling signal encounters a discontinuity in the transmission parameters of the line, or at the far end of the line if the line is not correctly terminated
Electrical termination
Electrical termination of a signal involves providing a terminator at the end of a wire or cable to prevent an RF signal from being reflected back from the end, causing interference...
in its characteristic impedance
Characteristic impedance
The characteristic impedance or surge impedance of a uniform transmission line, usually written Z_0, is the ratio of the amplitudes of a single pair of voltage and current waves propagating along the line in the absence of reflections. The SI unit of characteristic impedance is the ohm...
. This can happen, for instance, if two lengths of dissimilar transmission lines are joined together.
This article is about signal reflection
Signal reflection
Signal reflection occurs when a signal is transmitted along a transmission medium, such as a copper cable or an optical fiber, some of the signal power may be reflected back to its origin rather than being carried all the way along the cable to the far end. This happens because imperfections in the...
s on electrically conducting lines. Such lines are loosely referred to as copper
Copper
Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish...
lines, and indeed, in telecommunications are generally made from copper, but other metals are used, notably aluminium
Aluminium
Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances....
in power lines. Although this article is limited to describing reflections on conducting lines, this is essentially the same phenomenon as optical reflections in fibre-optic lines and microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
reflections in waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
s.
Reflections cause several undesirable effects, including modifying frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
s, causing overload
Overload
-Bands:* Overload * Overload * Overload -Albums:*Overload *Overload *Overload -Songs:*Overload , a dance song by Voodoo and Serano...
power in transmitter
Transmitter
In electronics and telecommunications a transmitter or radio transmitter is an electronic device which, with the aid of an antenna, produces radio waves. The transmitter itself generates a radio frequency alternating current, which is applied to the antenna. When excited by this alternating...
s and overvoltage
Overvoltage
When the voltage in a circuit or part of it is raised above its upper design limit, this is known as overvoltage. The conditions may be hazardous...
s on power line
Power Line
Power Line is an American political blog, providing news and commentary from a conservative point-of-view. It was originally written by three lawyers who attended Dartmouth College together: John H. Hinderaker, Scott W. Johnson, and Paul Mirengoff...
s. However, the reflection phenomenon can also be made use of in such devices as stubs and impedance transformers
Quarter wave impedance transformer
A quarter-wave impedance transformer, often written as λ/4 impedance transformer, is a component used in electrical engineering consisting of a length of transmission line or waveguide exactly one-quarter of a wavelength long and terminated in some known impedance. The device presents at its...
.
Specific cases
There are several approaches to understanding reflections, but the relationship of reflections to the conservation lawConservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s is particularly enlightening. A simple example is a step voltage,
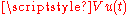, applied to one end of a lossless line, and consider what happens when the line is terminated in various ways. The step will be propagated down the line according to the telegrapher's equation at some velocity and the incident voltage at some point on the line is given by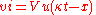The incident current in the line is given by the characteristic impedance
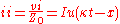
Open circuit line
The incident wave travelling down the line is not affected in any way by the open circuit at the end of the line. It cannot have any effect until the step actually reaches that point. The signal cannot have any foreknowledge of what is at the end of the line and is only affected by the local characteristics of the line. However, if the line is of length the step will arrive at the open circuit at time 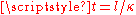, at which point the current in the line is zero (by the definition of an open circuit). Since charge continues to arrive at the end of the line through the incident current, but no current is leaving the line, then conservation of electric charge requires that there must be an equal and opposite current into the end of the line. Essentially, this is Kirchhoff's current lawKirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
in operation. This equal and opposite current is the reflected current,
, and sincethere must also be a reflected voltage,
, to drive the reflected current down the line. This reflected voltage must exist by reason of conservation of energy. The source is supplying energy to the line at a rate of . None of this energy is dissipated in the line or its termination and it must go somewhere. The only available direction is back up the line. Since the reflected current is equal in magnitude to the incident current, it must also be so that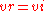These two voltages will add to each other so that after the step has been reflected, twice the incident voltage appears across the output terminals of the line. As the reflection proceeds back up the line the reflected voltage continues to add to the incident voltage and the reflected current continues to subtract from the incident current. After a further interval of
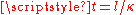the reflected step arrives at the generator end and the condition of double voltage and zero current will pertain there also as well as all along the length of the line. If the generator is matched to the line with an impedance of 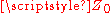the step transient will be absorbed in the generator internal impedance and there will be no further reflections.This doubling of voltage is a problem frequently arising when switching operations are carried out on power grids. A brief open circuit while switching is in progress will cause such a reflection and a voltage "spike" results. This counter-intuitive result may become clearer if the circuit voltages are considered when the line is so short that it can be ignored for the purposes of analysis. The equivalent circuit of a generator matched to a load
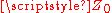to which it is delivering a voltage can be represented as in figure 2. That is, the generator can be represented as an ideal voltage generator of twice the voltage it is to deliver and an internal impedance of 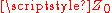.However if the generator is left open circuit, a voltage of
appears at the generator output terminals as in figure 3. The same situation pertains if a very short transmission line is inserted between the generator and the open circuit. If, however, a longer line with a characteristic impedance of 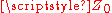and noticeable end-to-end delay is inserted, the generator – being initially matched to the impedance of the line – will have at the output. But after an interval, a reflected transient will return from the end of the line with the "information" on what the line is actually terminated with, and the voltage will become as before.Short circuit line
The reflection from a short-circuited line can be described in similar terms to that from an open-circuited line. Just as in the open circuit case the current must be zero at the end of the line, in the short circuit case the voltage must be zero since there can be no volts across a short circuit. Again, all of the energy must be reflected back up the line and the reflected voltage must be equal and opposite to the incident voltage by Kirchhoff's voltage lawKirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
:
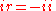
and,As the reflection travels back up the line, the two voltages subtract and cancel, while the currents will add (the reflection is double negative - a negative current travelling in the reverse direction), the dual situation to the open circuit case.
Arbitrary impedance
For the general case of a line terminated in some arbitrary impedance it is usual to describe the signal as a waveWave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
travelling down the line and analyse it in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. The impedance is consequently represented as a frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
dependant complex function.
For a line terminated in its own characteristic impedance there is no reflection. By definition, terminating in the characteristic impedance has the same effect as an infinitely long line. Any other impedance will result in a reflection. The magnitude of the reflection will be smaller than the magnitude of the incident wave if the terminating impedance is wholly or partly resistive since some of the energy of the incident wave will be absorbed in the resistance. The voltage across the terminating impedance may be calculated by replacing the output of the line with an equivalent generator (figure 4) and is given by
The reflection,
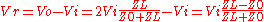
must be the exact amount required to make ,The reflection coefficient is defined as
and substituting in the expression for
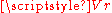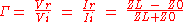
,In general
is a complex function but the above expression shows that the magnitude is limited to when 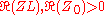The physical interpretation of this is that the reflection cannot be greater than the incident wave when only passive elements are involved (but see negative resistance amplifier for an example where this condition does not hold). For the special cases described above,
| Termination |  |
|---|---|
| Open circuit |  |
| Short circuit |  |
  |
  |
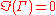When both
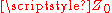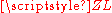and are purely resistive then must be purely real. In the general case when is complex, this is to be interpreted as a shift in phasePhase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
of the reflected wave relative to the incident wave.
Reactive termination
Another special case occurs when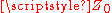 is purely real and 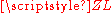is purely imaginary, , that is, it is a reactanceReactance
Reactance is the opposition of a circuit element to a change of electric current or voltage, due to that element's capacitance or inductance. A built-up electric field resists the change of voltage on the element, while a magnetic field resists the change of current...
. In this case,
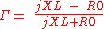
Since
then
showing that all the incident wave is reflected, and none of it is absorbed in the termination, as is to be expected from a pure reactance. There is, however, a change of phase in the reflection given by
Discontinuity along line
A discontinuity, or mismatch, somewhere along the length of the line results in part of the incident wave being reflected and part being transmitted onward in the second section of line as shown in figure 5. The reflection coefficient in this case is given byIn a similar manner, a transmission coefficient can be defined to describe the portion of the wave that it is transmitted in the forward direction:
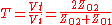
Another kind of discontinuity is caused when both sections of line have an identical characteristic impedance but there is a lumped element at the discontinuity. For the example shown (figure 6) of a shunt lumped element,
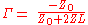
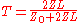
Similar expressions can be developed for a series element, or any electrical network for that matter.
Networks
Reflections in more complex scenarios, such as found on a network of cables, can result in very complicated and long lasting waveforms on the cable. Even a simple overvoltage pulse entering a cable system as uncomplicated as the power wiring found in a typical private home can result in an oscillatory disturbance as the pulse is reflected to and fro from multiple circuit ends. These ring waves as they are known persist for far longer than the original pulse and their waveforms bears little obvious resemblance to the original disturbance, containing high frequency components in the tens of MHz range.Standing waves
The phase of the reflected wave is continually changing with distance, with respect to the incident wave, as it proceeds back down the line. Because of this continuous change there are certain points on the line that the reflection will be in phase with the incident wave and the amplitudeAmplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the two waves will add. There will be other points where the two waves are in anti-phase and will consequently subtract. At these latter points the amplitude is at a minimum and they are known as nodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
. If the incident wave has been totally reflected and the line is lossless, there will be complete cancellation at the nodes with zero signal present there despite the ongoing transmission of waves in both directions. The points where the waves are in phase are anti-nodes and represent a peak in amplitude. Nodes and anti-nodes alternate along the line and the combined wave amplitude varies continuously between them. The combined (incident plus reflected) wave appears to be standing still on the line and is called a standing wave
Standing wave
In physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
.
The incident wave can be characterised in terms of the line's propagation constant
Propagation constant
The propagation constant of an electromagnetic wave is a measure of the change undergone by the amplitude of the wave as it propagates in a given direction. The quantity being measured can be the voltage or current in a circuit or a field vector such as electric field strength or flux density...
,
, source voltage, and distance from the source, , byHowever, it is often more convenient to work in terms of distance from the load () and the incident voltage that has arrived there (
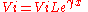
).The exponent is positive because
is measured in the reverse direction back up the line and the voltage is increasing closer to the source. Likewise the reflected voltage is given byThe total voltage on the line is given by
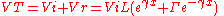
It is often convenient to express this in terms of hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s
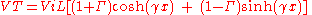
Similarly, the total current on the line is
The voltage nodes (current nodes are not at the same locations) and anti-nodes occur when
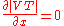
This does not have an easy analytical solution in the general case, but in the case of lossless lines (or lines that are short enough to be considered so)
can be replaced by where is the phase change constant. The voltage equation then reduces to trigonometric functions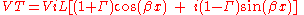and the partial differential of the magnitude of this yields the condition,
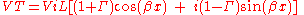
Expressing
in terms of wavelength, , allows to be solved in terms of : is purely real when the termination is short circuit or open circuit, or when both 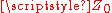and are purely resistive. In those cases the nodes and anti-nodes are given bywhich solves for
at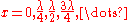For
the first point is a node, for the first point is an anti-node and thenceforth they will alternate. For terminations that are not purely resistive the spacing and alternation remain the same but the whole pattern is shifted along the line by a constant amount related to the phase of .Voltage standing wave ratio
The ratio of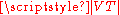 at anti-nodes and nodes is called the voltage standing wave ratio (VSWR) and is related to the reflection coefficient byfor a lossless line. For a lossy line the expression is only valid adjacent to the termination; VSWR asymptotically
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
approaches unity with distance from the termination or discontinuity.
VSWR and the positions of the nodes are parameters that can be directly measured with an instrument called a slotted line. This instrument makes use of the reflection phenomenon to make many different measurements at microwave frequencies. One use is that VSWR and node position can be used to calculate the impedance of a test component terminating the slotted line. This is a useful method because measuring impedances by directly measuring voltages and currents is difficult at these frequencies.
Input impedance
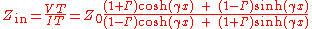
The input impedance looking into a transmission line which is not terminated with its characteristic impedance at the far will be something other than and will be a function of the length of the line. The value of this impedance can be found by dividing the expression for total voltage by the expression for total current given above:Substituting
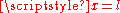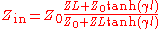
, the length of the line and dividing through by reduces this toAs before, when considering just short pieces of transmission line,
can be replaced by and the expression reduces to trigonometric functions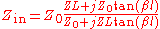Applications
There are two structures that are of particular importance which use reflected waves to modify impedance. One is the stub which is a short length of line terminated in a short-circuit (or it can be an open-circuit). This produces a purely imaginary impedance at its input, that is, a reactanceBy suitable choice of length, the stub can be used in place of a capacitor, an inductor or a resonant circuit.
The other structure is the quarter wave impedance transformer
Quarter wave impedance transformer
A quarter-wave impedance transformer, often written as λ/4 impedance transformer, is a component used in electrical engineering consisting of a length of transmission line or waveguide exactly one-quarter of a wavelength long and terminated in some known impedance. The device presents at its...
. As its name suggests, this is a line exactly
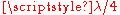in length. Since 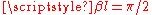this will produce the inverse of its terminating impedance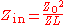Both of these structures are widely used in distributed element filter
Distributed element filter
A distributed element filter is an electronic filter in which capacitance, inductance and resistance are not localised in discrete capacitors, inductors and resistors as they are in conventional filters. Its purpose is to allow a range of signal frequencies to pass, but to block others...
s and impedance matching
Impedance matching
In electronics, impedance matching is the practice of designing the input impedance of an electrical load to maximize the power transfer and/or minimize reflections from the load....
networks.