Relativistic electromagnetism
Encyclopedia
Relativistic electromagnetism is a modern teaching strategy for developing electromagnetic field
theory from Coulomb’s law and Lorentz transformation
s. Though Coulomb’s law expresses action at a distance
, it is an easily understood electric force principle. The more sophisticated view of electromagnetism
expressed by electromagnetic fields in spacetime
can be approached by applying spacetime symmetries. In certain special configurations it is possible to exhibit magnetic effects due to relative charge density in various simultaneous hyperplanes. This approach to physics education
and the education and training of electrical and electronics engineers
can be seen in the Encyclopædia Britannica (1956), The Feynman Lectures on Physics
(1964), Edward M. Purcell (1965), Jack R. Tessman (1966), W.G.V. Rosser (1968), Anthony French
(1968), and Dale R. Corson
& Paul Lorrain (1970). This approach provides some preparation for understanding of magnetic forces involved in the Biot-Savart Law
, Ampère's law
, and Maxwell's equations
.
wrote to the Cleveland Physics Society on the occasion of a commemoration of the Michaelson–Morley experiment. In that letter he wrote:
This statement by Einstein reveals that he investigated spacetime symmetries to determine the complementarity of electric and magnetic forces.
, and how it looks from a different reference frame moving with respect to the first, is crucial to understand fields created by moving sources. In the special case, the sources that create the field are at rest with respect to one of the reference frames. Given the electric field
in the frame where the sources are at rest, Purcell asked: what is the electric field in some other frame?
He stated that the fundamental assumption is that, knowing the electric field at some point (in space and time) in the rest frame of the sources, and knowing the relative velocity
of the two frames provided all the information needed to calculate the electric field at the same point in the other frame. In other words, the electric field in the other frame does not depend on the particular distribution of the source charges
, only on the local value of the electric field in the first frame at that point. He assumed that the electric field is a complete representation of the influence of the far-away charges.
Alternatively, introductory treatments of magnetism
introduce the Biot-Savart law
, which describes the magnetic field associated with an electric current
. An observer at rest with respect to a system of static, free charges will see no magnetic field. However, a moving observer looking at the same set of charges does perceive a current, and thus a magnetic field.
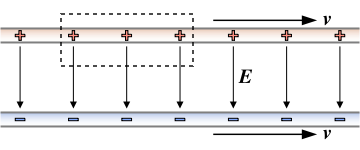Consider the very simple situation of a charged parallel-plate capacitor
, whose electric field (in its rest frame) is uniform (neglecting edge effects) between the plates and zero outside.
To calculate the electric field of this charge distribution in a reference frame where it is in motion, suppose that the motion is in a direction parallel to the plates as shown in figure 1. The plates will then be shorter by a factor of:
than they are in their rest frame, but the distance between them will be the same. Since charge is independent of the frame in which it is measured, the total charge on each plate is also the same. So the charge per unit area on the plates is therefore larger than in the rest frame by a factor of:
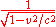
The field between the plates is therefore stronger by this factor.
Consider the electric field of a single, infinite plate of positive charge, moving parallel to itself. The field must be uniform both above and below the plate, since it is uniform
in its rest frame. We also assume that knowing the field in one frame is sufficient for calculating it in the other frame.
The plate however could have a non zero component of electric field in the direction of motion as in Fig 2a. Even in this case, the field of the infinite plane of negative charge must be equal and opposite to that of the positive plate (as in Fig 2b), since the combination of plates is neutral and cannot therefore produce any net fields. When the plates are separated, the horizontal components still cancel, and the resultant is a uniform vertical field as shown in Fig 1.
If Gauss's law is applied to pillbox as shown in Fig 1, it can be shown that the magnitude of the electric field between the plates is given by:
where the prime (') indicates the value measured in the frame in which the plates are moving.
represents the surface charge density of the positive plate. Since the plates are contracted in length by the factor
then the surface charge density in the primed frame is related to the value in the rest frame of the plates by:
But the electric field in the rest frame has value σ / ε0 and the field points in the same direction on both of the frames, so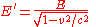
The E field in the primed frame is therefore stronger than in the unprimed frame. If the direction of motion is perpendicular to the plates, length contraction of the plates does not occur, but the distance between them is reduced. This closer spacing however does not affect the strength of the electric field. So for motion parallel to the electric field E,
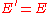
In the general case where motion is in a diagonal direction relative to the field the field is merely a superposition of the perpendicular and parallel fields., each generated by a set of plates at right angles to each other as shown in Fig 3. Since both sets of plates are length contracted, the two components of the E field are
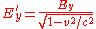
and
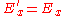
where the y subscript denotes perpendicular, and the x subscript, parallel.
These transformation equations only apply if the source of the field is at rest in the unprimed frame.
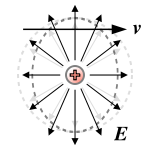A very important application of the electric field transformation equations is to the field of a single point charge moving with constant velocity. In its rest frame, the electric field of a positive point charge has the same strength in all directions and points directly away from the charge. In some other reference frame the field will appear differently.
In applying the transformation equations to a nonuniform electric field, it is important to record not only of the value of the field, but also at what point in space it has this value.
In the rest frame of the particle, the point charge can be imagined to be surrounded by a spherical shell which is also at rest. In our reference frame, however, both the particle and its sphere are moving. Length contraction therefore states that the sphere
is deformed into a spheroid
, as shown in cross section
in Fig 4.
Consider the value of the electric field at any point on the surface
of the sphere. Let x and y be the components of the displacement
(in the rest frame of the charge), from the charge to a point on the sphere, measured parallel
and perpendicular to the direction of motion as shown in the figure. Because the field in the rest frame of the charge points directly away from the charge, its components are in the same ratio as the components of the displacement:
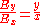
In our reference frame, where the charge is moving, the displacement x' in the direction of motion is length-contracted:
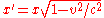
The electric field at any point on the sphere points directly away from the charge. (b) In a reference frame where the charge and the sphere are moving to the right, the sphere is length-contracted but the vertical component of the field is stronger. These two effects combine to make the field again point directly away from the current location of the charge. (While the y component of the displacement is the same in both frames).
However, according to the above results, the y component of the field is enhanced by a similar factor:
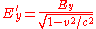
whilst the x component of the field is the same in both frames. The ratio of the field components is therefore
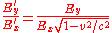
So, the field in the primed frame points directly away from the charge, just as in the unprimed frame.
A view of the electric field of a point charge moving at constant velocity is shown in figure 4. The faster the charge is moving, the more noticeable the enhancement of the perpendicular component of the field becomes. If the speed of the charge is much less than the speed of light, this enhancement is often negligible. But under certain circumstances, it is crucially important even at low velocities.
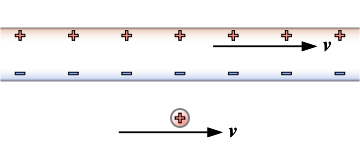In the simple model of events in a wire stretched out horizontally, a current can be represented by the evenly spaced positive charges, moving to the right, whilst an equal number of negative charges remain at rest. If the wire is electrostatically neutral, the distance between adjacent positive charges must be the same as the distance between adjacent negative charges.
Assume a positively charged particle, with charge Q, outside the wire and traveling (initially) in a direction parallel to the current (Figure 5). This particle is the test charge. Assume the speed of the test charge to be v, the same as the speed of the moving charges in the wire. The test charge should experience a magnetic force as can be easily confirmed by experiment.
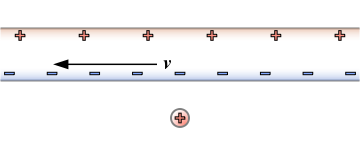In this situation where both the source charges and the test charge are moving, we consider what happens in a different reference frame, for simplicity. Consider a reference frame where the test charge is at rest, at least initially (Figure 6). The reference frame is the 'test charge frame' and the original reference frame was the 'lab frame'.
In the 'test charge frame' the only possible force is the electrostatic force QE, since the electric field is defined as the force exerted on a unit positive test charge that is at rest. The same situation as in the fig, but viewed from the reference frame in which the test charge is initially at rest. Here the positive charges in the wire are at rest while the negative charges in the wire are moving to the left. The distance between the negative charges is 'length-contracted' relative to the lab frame, while the distance between the positive charges is not 'length-contracted', so the wire carries a net negative charge. The situation in the test charge frame is shown in the figure. The positive charges in the wire are also at rest, but the negative charges in the wire are moving to the left with speed v.
If we now consider length contraction, the negative charges are at rest in the lab frame but moving in the frame of the test charge, so the distance between these negative charges is smaller in the test charge frame than in the lab frame. Their average separation is given by:
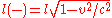
Conversely, the positive charges are moving in the lab frame but at rest in the test charge frame. So the distance between the positive charges is larger in the test charge frame than in the lab frame.
Their separation in the test charge frame is:
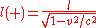
Both of these effects combine to give the wire a net negative charge in the frame of test charge. Now it is known that a negatively charged wire exerts an attractive force on a positively charged particle. The test charge will therefore be attracted and will move toward the wire.
If the currents are in opposite directions, consider the charge moving to the left. No charges are now at rest in the reference frame of the test charge. The negative charges are moving with speed v in the test charge frame so their spacing is again:
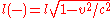
The distance between positive charges is more difficult to calculate. The relative velocity should be less than 2v due to special relativity. For simplicity, assume it is 2v. The positive charge spacing contraction is then:
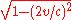
relative to its value in their rest frame. Now its value in their rest frame was found to be
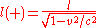
So the final spacing of positive charges is:
To determine whether l(+) or l(-) is larger we assume that v<<c and use the binomial approximation that
After some algebraic calculation it is found that l(+) < l(-), and so the wire is positively charged in the frame of the test charge.
where is the distance between them in the lab frame. Similarly, the distance between the positive charges is not length-contracted:
Both of these effects give the wire a net negative charge in the test charge frame, so that it exerts an attractive force on the test charge.
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
theory from Coulomb’s law and Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s. Though Coulomb’s law expresses action at a distance
Action at a distance (physics)
In physics, action at a distance is the interaction of two objects which are separated in space with no known mediator of the interaction. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant...
, it is an easily understood electric force principle. The more sophisticated view of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
expressed by electromagnetic fields in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
can be approached by applying spacetime symmetries. In certain special configurations it is possible to exhibit magnetic effects due to relative charge density in various simultaneous hyperplanes. This approach to physics education
Physics education
Physics education or physics education research refers both to the methods currently used to teach physics and to an area of pedagogical research that seeks to improve those methods. Historically, physics has been taught at the high school and college level primarily by the lecture method...
and the education and training of electrical and electronics engineers
Education and training of electrical and electronics engineers
Both electrical and electronics engineers typically possess an academic degree with a major in electrical/ electronics engineering. The length of study for such a degree is usually three or four years and the completed degree may be designated as a Bachelor of Engineering, Bachelor of Science or...
can be seen in the Encyclopædia Britannica (1956), The Feynman Lectures on Physics
The Feynman Lectures on Physics
The Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
(1964), Edward M. Purcell (1965), Jack R. Tessman (1966), W.G.V. Rosser (1968), Anthony French
Anthony French
Anthony Philip French is an emeritus professor of physics at the Massachusetts Institute of Technology. He was born in Brighton, England....
(1968), and Dale R. Corson
Dale R. Corson
Dale R. Corson was the eighth president of Cornell University. Born in Pittsburg, Kansas, in 1914, Corson received a B.A. degree from the College of Emporia in 1934, his M.A. degree from the University of Kansas in 1935, and his Ph.D...
& Paul Lorrain (1970). This approach provides some preparation for understanding of magnetic forces involved in the Biot-Savart Law
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
, Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
, and Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
Einstein’s motivation
In 1953 Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
wrote to the Cleveland Physics Society on the occasion of a commemoration of the Michaelson–Morley experiment. In that letter he wrote:
- What led me more or less directly to the special theory of relativity was the conviction that the electromotive force acting on a body in motion in a magnetic field was nothing else but an electric field.
This statement by Einstein reveals that he investigated spacetime symmetries to determine the complementarity of electric and magnetic forces.
Introduction
Purcell argued that the question of an electric field in one inertial frame of referenceInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
, and how it looks from a different reference frame moving with respect to the first, is crucial to understand fields created by moving sources. In the special case, the sources that create the field are at rest with respect to one of the reference frames. Given the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
in the frame where the sources are at rest, Purcell asked: what is the electric field in some other frame?
He stated that the fundamental assumption is that, knowing the electric field at some point (in space and time) in the rest frame of the sources, and knowing the relative velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the two frames provided all the information needed to calculate the electric field at the same point in the other frame. In other words, the electric field in the other frame does not depend on the particular distribution of the source charges
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
, only on the local value of the electric field in the first frame at that point. He assumed that the electric field is a complete representation of the influence of the far-away charges.
Alternatively, introductory treatments of magnetism
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
introduce the Biot-Savart law
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
, which describes the magnetic field associated with an electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
. An observer at rest with respect to a system of static, free charges will see no magnetic field. However, a moving observer looking at the same set of charges does perceive a current, and thus a magnetic field.
Uniform electric field — simple analysis
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
, whose electric field (in its rest frame) is uniform (neglecting edge effects) between the plates and zero outside.
To calculate the electric field of this charge distribution in a reference frame where it is in motion, suppose that the motion is in a direction parallel to the plates as shown in figure 1. The plates will then be shorter by a factor of:
than they are in their rest frame, but the distance between them will be the same. Since charge is independent of the frame in which it is measured, the total charge on each plate is also the same. So the charge per unit area on the plates is therefore larger than in the rest frame by a factor of:
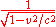
The field between the plates is therefore stronger by this factor.
More rigorous analysis
Uniform
A uniform is a set of standard clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are worn by armed forces and paramilitary organizations such as police, emergency services, security guards, in some workplaces and schools and by inmates...
in its rest frame. We also assume that knowing the field in one frame is sufficient for calculating it in the other frame.
The plate however could have a non zero component of electric field in the direction of motion as in Fig 2a. Even in this case, the field of the infinite plane of negative charge must be equal and opposite to that of the positive plate (as in Fig 2b), since the combination of plates is neutral and cannot therefore produce any net fields. When the plates are separated, the horizontal components still cancel, and the resultant is a uniform vertical field as shown in Fig 1.
If Gauss's law is applied to pillbox as shown in Fig 1, it can be shown that the magnitude of the electric field between the plates is given by:
where the prime (') indicates the value measured in the frame in which the plates are moving.
represents the surface charge density of the positive plate. Since the plates are contracted in length by the factorthen the surface charge density in the primed frame is related to the value in the rest frame of the plates by:
But the electric field in the rest frame has value σ / ε0 and the field points in the same direction on both of the frames, so
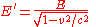
The E field in the primed frame is therefore stronger than in the unprimed frame. If the direction of motion is perpendicular to the plates, length contraction of the plates does not occur, but the distance between them is reduced. This closer spacing however does not affect the strength of the electric field. So for motion parallel to the electric field E,
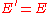
In the general case where motion is in a diagonal direction relative to the field the field is merely a superposition of the perpendicular and parallel fields., each generated by a set of plates at right angles to each other as shown in Fig 3. Since both sets of plates are length contracted, the two components of the E field are
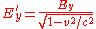
and
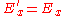
where the y subscript denotes perpendicular, and the x subscript, parallel.
These transformation equations only apply if the source of the field is at rest in the unprimed frame.
The field of a moving point charge
In applying the transformation equations to a nonuniform electric field, it is important to record not only of the value of the field, but also at what point in space it has this value.
In the rest frame of the particle, the point charge can be imagined to be surrounded by a spherical shell which is also at rest. In our reference frame, however, both the particle and its sphere are moving. Length contraction therefore states that the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is deformed into a spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
, as shown in cross section
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
in Fig 4.
Consider the value of the electric field at any point on the surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
of the sphere. Let x and y be the components of the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
(in the rest frame of the charge), from the charge to a point on the sphere, measured parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
and perpendicular to the direction of motion as shown in the figure. Because the field in the rest frame of the charge points directly away from the charge, its components are in the same ratio as the components of the displacement:
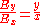
In our reference frame, where the charge is moving, the displacement x' in the direction of motion is length-contracted:
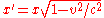
The electric field at any point on the sphere points directly away from the charge. (b) In a reference frame where the charge and the sphere are moving to the right, the sphere is length-contracted but the vertical component of the field is stronger. These two effects combine to make the field again point directly away from the current location of the charge. (While the y component of the displacement is the same in both frames).
However, according to the above results, the y component of the field is enhanced by a similar factor:
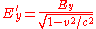
whilst the x component of the field is the same in both frames. The ratio of the field components is therefore
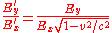
So, the field in the primed frame points directly away from the charge, just as in the unprimed frame.
A view of the electric field of a point charge moving at constant velocity is shown in figure 4. The faster the charge is moving, the more noticeable the enhancement of the perpendicular component of the field becomes. If the speed of the charge is much less than the speed of light, this enhancement is often negligible. But under certain circumstances, it is crucially important even at low velocities.
The origin of magnetic forces
Assume a positively charged particle, with charge Q, outside the wire and traveling (initially) in a direction parallel to the current (Figure 5). This particle is the test charge. Assume the speed of the test charge to be v, the same as the speed of the moving charges in the wire. The test charge should experience a magnetic force as can be easily confirmed by experiment.
In the 'test charge frame' the only possible force is the electrostatic force QE, since the electric field is defined as the force exerted on a unit positive test charge that is at rest. The same situation as in the fig, but viewed from the reference frame in which the test charge is initially at rest. Here the positive charges in the wire are at rest while the negative charges in the wire are moving to the left. The distance between the negative charges is 'length-contracted' relative to the lab frame, while the distance between the positive charges is not 'length-contracted', so the wire carries a net negative charge. The situation in the test charge frame is shown in the figure. The positive charges in the wire are also at rest, but the negative charges in the wire are moving to the left with speed v.
If we now consider length contraction, the negative charges are at rest in the lab frame but moving in the frame of the test charge, so the distance between these negative charges is smaller in the test charge frame than in the lab frame. Their average separation is given by:
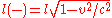
Conversely, the positive charges are moving in the lab frame but at rest in the test charge frame. So the distance between the positive charges is larger in the test charge frame than in the lab frame.
Their separation in the test charge frame is:
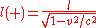
Both of these effects combine to give the wire a net negative charge in the frame of test charge. Now it is known that a negatively charged wire exerts an attractive force on a positively charged particle. The test charge will therefore be attracted and will move toward the wire.
If the currents are in opposite directions, consider the charge moving to the left. No charges are now at rest in the reference frame of the test charge. The negative charges are moving with speed v in the test charge frame so their spacing is again:
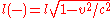
The distance between positive charges is more difficult to calculate. The relative velocity should be less than 2v due to special relativity. For simplicity, assume it is 2v. The positive charge spacing contraction is then:
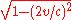
relative to its value in their rest frame. Now its value in their rest frame was found to be
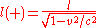
So the final spacing of positive charges is:
To determine whether l(+) or l(-) is larger we assume that v<<c and use the binomial approximation that
After some algebraic calculation it is found that l(+) < l(-), and so the wire is positively charged in the frame of the test charge.
The Lorentz force law
A test charge near a wire carrying current will experience a magnetic force dependent on the velocity of the moving charges in the wire. If the current is flowing to the right, and a positive test charge is below the wire, then there is a force in a direction 90° counterclockwise from the direction of motion.The magnetic field of a wire
Calculation of the magnitude of the force exerted by a current-carrying wire on a moving charge is equivalent to calculating the magnetic field produced by the wire. Consider again the situation shown in figures. The latter figure, showing the situation in the reference frame of the test charge, is reproduced in the figure. The positive charges in the wire, each with charge q, are at rest in this frame, while the negative charges, each with charge −q, are moving to the left with speed v. The average distance between the negative charges in this frame is length-contracted to:where is the distance between them in the lab frame. Similarly, the distance between the positive charges is not length-contracted:
Both of these effects give the wire a net negative charge in the test charge frame, so that it exerts an attractive force on the test charge.
See also
- Formulation of Maxwell's equations in special relativityFormulation of Maxwell's equations in special relativityThe covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...
- Special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
- ElectromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
- Liénard-Wiechert potentialsLiénard-Wiechert PotentialsLiénard-Wiechert potentials describe the classical electromagnetic effect of a moving electric point charge in terms of a vector potential and a scalar potential...
- Wheeler-Feynman absorber theory