
Relaxation method
Encyclopedia
In numerical mathematics, relaxation methods are iterative method
s for solving systems of equations
, including nonlinear systems.
Relaxation methods were developed for solving large sparse
linear system
s, which arose as finite-difference
discretization
s of differential equation
s. They are also used for the solution of linear equations for linear least-squares problems and also for systems of linear inequalities, such as those arising in linear programming
. They have also been developed for solving nonlinear systems of equations.
Relaxation methods are important especially in the solution linear systems used to model elliptic partial differential equations, such as Laplace's equation
and its generalization, Poisson's equation
. These equations describe boundary-value problems, in which the solution-function 's values are specified on boundary of a domain; the problem is to compute a solution also on its interior. Relaxation methods are used to solve the linear equations resulting from a discretization of the differential equation, for example by finite differences.
These iterative methods of relaxation should not be confused with "relaxations" in mathematical optimization, which approximate
a difficult problem by a simpler problem, whose "relaxed" solution provides information about the solution of the original problem.
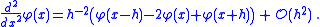
Using this in both dimensions for a function φ of two arguments at the point (x, y), and solving for φ(x, y), results in: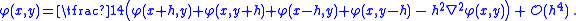
To approximate the solution of the Poisson equation: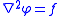
numerically on a two-dimensional grid with grid spacing h, the relaxation method assigns the given values of function φ to the grid points near the boundary and arbitrary values to the interior grid points, and then repeatedly performs the assignment
φ := φ* on the interior points, where φ* is defined by: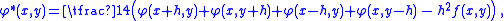
until convergence.
The method, sketched here for two dimensions, is readily generalized to other numbers of dimensions.
s for new methods. Indeed, the choice of preconditioner is often more important than the choice of iterative method, according to Yousef Saad
.
Multigrid methods may be used to accelerate the methods. One can first compute an approximation on a coarser grid – usually the double spacing 2h – and use that solution with interpolated
values for the other grid points as the initial assignment. This can then also be done recursively for the coarser computation.
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s for solving systems of equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
, including nonlinear systems.
Relaxation methods were developed for solving large sparse
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s, which arose as finite-difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
discretization
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
s of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. They are also used for the solution of linear equations for linear least-squares problems and also for systems of linear inequalities, such as those arising in linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. They have also been developed for solving nonlinear systems of equations.
Relaxation methods are important especially in the solution linear systems used to model elliptic partial differential equations, such as Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
and its generalization, Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
. These equations describe boundary-value problems, in which the solution-function 's values are specified on boundary of a domain; the problem is to compute a solution also on its interior. Relaxation methods are used to solve the linear equations resulting from a discretization of the differential equation, for example by finite differences.
These iterative methods of relaxation should not be confused with "relaxations" in mathematical optimization, which approximate
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
a difficult problem by a simpler problem, whose "relaxed" solution provides information about the solution of the original problem.
Model problem of potential theory
When φ is a smooth real-valued function on the real numbers, its second derivative can be approximated by: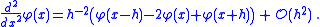
Using this in both dimensions for a function φ of two arguments at the point (x, y), and solving for φ(x, y), results in:
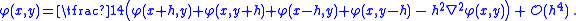
To approximate the solution of the Poisson equation:
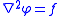
numerically on a two-dimensional grid with grid spacing h, the relaxation method assigns the given values of function φ to the grid points near the boundary and arbitrary values to the interior grid points, and then repeatedly performs the assignment
φ := φ* on the interior points, where φ* is defined by:
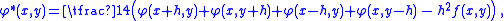
until convergence.
The method, sketched here for two dimensions, is readily generalized to other numbers of dimensions.
Convergence and acceleration
While the method converges under general conditions, it typically makes slower progress than competing methods. Nonetheless, the study of relaxation methods remains a core part of linear algebra, because the transformations of relaxation theory provide excellent preconditionerPreconditioner
In mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...
s for new methods. Indeed, the choice of preconditioner is often more important than the choice of iterative method, according to Yousef Saad
Yousef Saad
Yousef Saad is an I.T. Distinguished Professor of Computer Science in the Department of Computer Science and Engineering at the University of Minnesota. He holds the William Norris Chair for Large-Scale Computing since January 2006...
.
Multigrid methods may be used to accelerate the methods. One can first compute an approximation on a coarser grid – usually the double spacing 2h – and use that solution with interpolated
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
values for the other grid points as the initial assignment. This can then also be done recursively for the coarser computation.
See also
- The Jacobi methodJacobi methodIn numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
is a simple relaxation method. - The Gauss–Seidel method is an improvement upon the Jacobi method.
- Successive over-relaxationSuccessive over-relaxationIn numerical linear algebra, the method of successive over-relaxation is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.It was devised simultaneously by David...
can be applied to either of the Jacobi and Gauss–Seidel methods to speed convergence. - Multigrid methods
Further reading
- Southwell, R.V. (1940) Relaxation Methods in Engineering Science. Oxford University Press, Oxford.
- Southwell, R.V. (1946) Relaxation Methods in Theoretical Physics. Oxford University Press, Oxford.

