Residuated mapping
Encyclopedia
In mathematics, the concept of a residuated mapping arises in the theory of partially ordered set
s. It refines the concept of a monotone function
.
If A, B are posets
, a function f: A → B is defined to be monotone if and only if it is order-preserving: that is, x ≤ y implies f(x) ≤ f(y). This is equivalent to the condition that the preimage under f of every down-set of B is a down-set of A. We define a principal down-set to be one of the form ↓{b} = { b' ∈ B : b' ≤ b }. In general the preimage of a principal down-set need not be a principal down-set.
The notion of residuated map can be generalized to a binary operator (or any higher arity
) via component-wise residuation. This approach gives rise to notions of left and right division in a partially ordered magma
, additionally endowing it with a quasigroup
structure. (One speaks only of residuated algebra for higher arities). A binary (or higher arity) residuated map is usually not residuated as a unary map.
It can be shown that f is residuated if and only if there exists a unique monotone function f +: B → A such that f o f + ≤ idB and f + o f ≥ idA, where id is the identity function
. The function f + is the residual of f. A residuated function and its residual form a Galois connection
under the (more recent) monotone definition of that concept, and for every (monotone) Galois connection the lower adjoints is residuated with the residual being the upper adjoint. Therefore, the notions of monotone Galois connection and residuated mapping essentially coincide.
Additionally, we have f -1(↓{b}) = ↓{f +(b)}.
If B° denotes the order dual (opposite poset) to B then f : A → B is a residuated mapping if and only if f : A → B° and f *: B° → A form a Galois connection
under the original antitone definition of this notion.
If f : A → B and g : B → C are residuated mappings, then so is the function composition
fg : A → C, with residual (fg) + = g +f +. The antitone Galois connections do not share this property.
The set of monotone transformations (functions) over a poset is an ordered monoid with the pointwise order, and so is the set of residuated transformations.
For example, every ordered group
is residuated, and the division defined by the above coincides with notion of division in a group. A less trivial example is the set Matn(B) of square matrices over a boolean algebra B, where the matrices are ordered pointwise
. The pointwise order endows Matn(B) with pointwise meets, joins and complements. Matrix multiplication
is defined in the usual manner with the "product" being a meet, and the "sum" a join. It can be shown that X\Y = (YtX’)’ and X/Y = (X’Yt)’, where (X’ is the complement of X, and Yt is the transposed matrix).
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s. It refines the concept of a monotone function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
.
If A, B are posets
Posets
Posets may refer to:*Posets peak, a mountain, second highest of the Pyrenees*Partially ordered sets...
, a function f: A → B is defined to be monotone if and only if it is order-preserving: that is, x ≤ y implies f(x) ≤ f(y). This is equivalent to the condition that the preimage under f of every down-set of B is a down-set of A. We define a principal down-set to be one of the form ↓{b} = { b
The notion of residuated map can be generalized to a binary operator (or any higher arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
) via component-wise residuation. This approach gives rise to notions of left and right division in a partially ordered magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
, additionally endowing it with a quasigroup
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
structure. (One speaks only of residuated algebra for higher arities). A binary (or higher arity) residuated map is usually not residuated as a unary map.
Definition
If A, B are posets, a function f: A → B is residuated if and only if the preimage under f of every principal down-set of B is a principal down-set of A.Consequences
With A, B posets, the set of functions A → B can be ordered by the pointwise order f ≤ g ↔ (∀x ∈ A) f(x) ≤ g(x).It can be shown that f is residuated if and only if there exists a unique monotone function f +: B → A such that f o f + ≤ idB and f + o f ≥ idA, where id is the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
. The function f + is the residual of f. A residuated function and its residual form a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
under the (more recent) monotone definition of that concept, and for every (monotone) Galois connection the lower adjoints is residuated with the residual being the upper adjoint. Therefore, the notions of monotone Galois connection and residuated mapping essentially coincide.
Additionally, we have f -1(↓{b}) = ↓{f +(b)}.
If B° denotes the order dual (opposite poset) to B then f : A → B is a residuated mapping if and only if f : A → B° and f *: B° → A form a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
under the original antitone definition of this notion.
If f : A → B and g : B → C are residuated mappings, then so is the function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
fg : A → C, with residual (fg) + = g +f +. The antitone Galois connections do not share this property.
The set of monotone transformations (functions) over a poset is an ordered monoid with the pointwise order, and so is the set of residuated transformations.
Examples
- The ceiling function
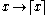from R to Z (with the usual order in each case) is residuated, with residual mapping the natural embedding of Z into R. - The embedding of Z into R is also residuated. Its residual is the floor functionFloor functionIn mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
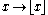Residuated binary operators
If • : P × Q → R is a binary map and P, Q, and R are posets, then one may define residuation component-wise for the left and right translations, i.e. multiplication by a fixed element. For an element x in P define xλ(y) = x • y, and for x in Q define λx(y) = y • x. Then • is said to be residuated if and only if xλ and λx are residuated for all x (in P and respectively Q). Left (and resp. right) division are defined by taking the residuals of the left (and resp. right) translations: x\y = (xλ)+(y) and x/y = (λx)+(y)For example, every ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
is residuated, and the division defined by the above coincides with notion of division in a group. A less trivial example is the set Matn(B) of square matrices over a boolean algebra B, where the matrices are ordered pointwise
Pointwise
In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
. The pointwise order endows Matn(B) with pointwise meets, joins and complements. Matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
is defined in the usual manner with the "product" being a meet, and the "sum" a join. It can be shown that X\Y = (YtX’)’ and X/Y = (X’Yt)’, where (X’ is the complement of X, and Yt is the transposed matrix).