
Restricted sumset
Encyclopedia
In additive number theory
and combinatorics
, a restricted sumset has the form

where are finite nonempty subsets of a field
are finite nonempty subsets of a field
 and
and  is a polynomial over
is a polynomial over  .
.
When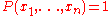 ,
, 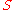 is the usual sumset
is the usual sumset
 which is denoted by
which is denoted by  if
if 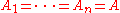 ; when
; when
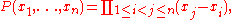
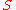 is written as
is written as  which is denoted by
which is denoted by 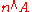 if
if 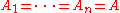 . Note that
. Note that 
if and only if there exist
with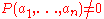 .
.
and Harold Davenport
asserts that for any prime and nonempty subsets
and nonempty subsets  and
and  of the field
of the field 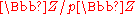 we have the inequality
we have the inequality
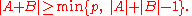
and Hans Heilbronn
in 1964 states that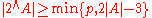 if
if 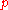 is a prime and
is a prime and  is a nonempty subset of the field
is a nonempty subset of the field  . This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994
. This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994
who showed that

where is a finite nonempty subset of a field
is a finite nonempty subset of a field  , and
, and 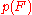 is a prime
is a prime  if
if  is of characteristic
is of characteristic 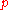 , and
, and 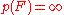 if
if  is of characteristic 0. Various extensions of this result were given by Noga Alon
is of characteristic 0. Various extensions of this result were given by Noga Alon
, M. B. Nathanson and I. Ruzsa
in 1996, Q. H. Hou and Zhi-Wei Sun
in 2002,
and G. Karolyi in 2004.
 be a polynomial over a field
be a polynomial over a field  .
.
Suppose that the coefficient of the monomial in
in  is nonzero and
is nonzero and  is the total degree of
is the total degree of  . If
. If  are finite subsets of
are finite subsets of  with
with  for
for  , then there are
, then there are 
such that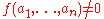 .
.
The method using the combinatorial Nullstellensatz is also called the polynomial method. This tool was rooted in a paper of N. Alon and M. Tarsi in 1989,
and developed by Alon, Nathanson and Ruzsa in 1995-1996,
and reformulated by Alon in 1999.
Additive number theory
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a restricted sumset has the form

where
 are finite nonempty subsets of a field
are finite nonempty subsets of a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 and
and  is a polynomial over
is a polynomial over  .
.When
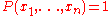 ,
, 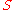 is the usual sumset
is the usual sumsetSumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
 which is denoted by
which is denoted by  if
if 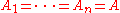 ; when
; when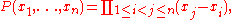
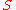 is written as
is written as  which is denoted by
which is denoted by 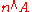 if
if 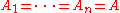 . Note that
. Note that 
if and only if there exist

with
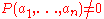 .
.Cauchy-Davenport theorem
The Cauchy–Davenport theorem named after Augustin Louis CauchyAugustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
and Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
asserts that for any prime
 and nonempty subsets
and nonempty subsets  and
and  of the field
of the field 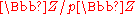 we have the inequality
we have the inequality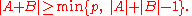
Erdős–Heilbronn conjecture
The Erdős–Heilbronn conjecture posed by Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Hans Heilbronn
Hans Heilbronn
Hans Arnold Heilbronn was a mathematician.He was born into a German-Jewish family. He was a student at the universities of Berlin, Freiburg and Göttingen, where he met Edmund Landau, who supervised his doctorate...
in 1964 states that
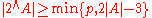 if
if 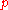 is a prime and
is a prime and  is a nonempty subset of the field
is a nonempty subset of the field  . This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994
. This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994who showed that

where
 is a finite nonempty subset of a field
is a finite nonempty subset of a field  , and
, and 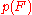 is a prime
is a prime  if
if  is of characteristic
is of characteristic 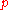 , and
, and 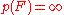 if
if  is of characteristic 0. Various extensions of this result were given by Noga Alon
is of characteristic 0. Various extensions of this result were given by Noga AlonNoga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
, M. B. Nathanson and I. Ruzsa
Imre Z. Ruzsa
Imre Z. Ruzsa is a Hungarian mathematician specializing in number theory.Ruzsa participated in the International Mathematical Olympiad for Hungary, winning a silver medal in 1969, and two consecutive gold medals with perfect scores in 1970 and 1971. He graduated from the Eötvös Loránd University...
in 1996, Q. H. Hou and Zhi-Wei Sun
Zhi-Wei Sun
Zhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
in 2002,
and G. Karolyi in 2004.
Combinatorial Nullstellensatz
A powerful tool in the study of lower bounds for cardinalities of various restricted sumsets is the following fundamental principle: the combinatorial Nullstellensatz. Let be a polynomial over a field
be a polynomial over a field  .
.Suppose that the coefficient of the monomial
 in
in  is nonzero and
is nonzero and  is the total degree of
is the total degree of  . If
. If  are finite subsets of
are finite subsets of  with
with  for
for  , then there are
, then there are 
such that
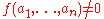 .
.The method using the combinatorial Nullstellensatz is also called the polynomial method. This tool was rooted in a paper of N. Alon and M. Tarsi in 1989,
and developed by Alon, Nathanson and Ruzsa in 1995-1996,
and reformulated by Alon in 1999.
External links
- Zhi-Wei SunZhi-Wei SunZhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
: On some conjectures of Erdős-Heilbronn, Lev and Snevily (PDF), a survey talk.

