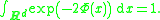Reversible diffusion
Encyclopedia
In mathematics
, a reversible diffusion is a specific example of a reversible
stochastic process
. Reversible diffusions have an elegant characterization
due to the Russia
n mathematician
Andrey Nikolaevich Kolmogorov.
al standard Brownian motion
; let b : Rd → Rd be a Lipschitz continuous vector field
. Let X : [0, +∞) × Ω → Rd be an Itō diffusion
defined on a probability space
(Ω, Σ, P) and solving the Itō stochastic differential equation
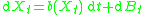
with square-integrable initial condition, i.e. X0 ∈ L2(Ω, Σ, P; Rd). Then the following are equivalent:
(Of course, the condition that b be the negative of the gradient
of Φ only determines Φ up to an additive constant; this constant may be chosen so that exp(−2Φ(·)) is a probability density function
with integral 1.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a reversible diffusion is a specific example of a reversible
Reversibility
Reversibility can refer to:* Reversible dynamics, a mathematical dynamical system, or physical laws of motion, for which time-reversed dynamics are well defined* Reversible diffusion, an example of a reversible stochastic process...
stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. Reversible diffusions have an elegant characterization
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
due to the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Andrey Nikolaevich Kolmogorov.
Kolmogorov's characterization of reversible diffusions
Let B denote a d-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al standard Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
; let b : Rd → Rd be a Lipschitz continuous vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. Let X : [0, +∞) × Ω → Rd be an Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
defined on a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) and solving the Itō stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
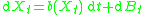
with square-integrable initial condition, i.e. X0 ∈ L2(Ω, Σ, P; Rd). Then the following are equivalent:
- The process X is reversible with stationary distributionStationary distributionStationary distribution may refer to:* The limiting distribution in a Markov chain* The marginal distribution of a stationary process or stationary time series* The set of joint probability distributions of a stationary process or stationary time series...
μ on Rd.
- There exists a scalar potentialScalar potentialA scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
Φ : Rd → R such that b = −∇Φ, μ has Radon–Nikodym derivative
(Of course, the condition that b be the negative of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of Φ only determines Φ up to an additive constant; this constant may be chosen so that exp(−2Φ(·)) is a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
with integral 1.)