Rhumb line
Encyclopedia
In navigation
, a rhumb line (or loxodrome) is a line crossing all meridians
of longitude
at the same angle, i.e. a path derived from a defined initial bearing
. That is, upon taking an initial bearing, one proceeds along the same bearing, without changing the direction as measured relative to true north
.
of certain navigational maps. A rhumb line appears as a straight line on a Mercator projection
map.
The name is derived from Old French: "rumb", a line on the chart which intersects all meridians at the same angle. On a plane surface this would be the shortest distance between two points. Over the Earth's surface at low latitudes or over short distances it can be used for plotting a vehicle, aircraft or ship's course. Over longer distances and/or at higher latitudes great circle
routes provide the shortest distances. However the inconvenience of having to continuously change bearings while travelling a great circle route makes rhumb line navigation appealing in certain instances.
The point can be illustrated with an East-West passage over 90 degrees of longitude along the equator
, for which the great-circle and rhumb-line distances are the same at 5400 nautical miles (10,000.8 km). At 20 degrees North the great-circle distance is 4997 miles (8,041.9 km) while the rhumb-line distance is 5074 miles (8,165.8 km), about 1½ percent further. But at 60 degrees North the great circle distance is 2485 miles (3,999.2 km) while the rhumb-line is 2700 miles (4,345.2 km), a difference of 8½ percent. A more extreme case is the air route between New York and Hong Kong, for which the rhumb-line path is 9700 nautical miles (17,964.4 km). The great-circle route over the North Pole is 7000 nautical miles (12,964 km), or 5½ hours less flying time at a typical cruising speed
.
Some old maps in the Mercator projection have grids composed of lines of latitude
and longitude
but also show rhumb lines which are oriented directly towards North, at a right angle from the North, or at some angle from the North which is some simple rational fraction of a right angle. These rhumb lines would be drawn so that they would converge at certain points of the map: lines going in every direction would converge at each of these points. See compass rose
. Such maps would necessarily have been in the Mercator projection therefore not all old maps would have been capable of showing rhumb-line markings.
The radial oriented lines on a compass rose are also called rhumbs. The expression "sailing on a rhumb" was used in the 16th–19th centuries to indicate a particular compass heading.
Some Muslim groups in North America face along the rhumb line to Mecca (southeastwards) as their qibla
(praying direction) instead of the most direct Great Circle path, which is northeastward from North America.
Early navigators in the time before the invention of the chronometer used rhumb-line courses on long ocean passages, because the ship's latitude could be established accurately by sightings of the Sun or stars but there was no accurate way to determine the longitude. The ship would sail North or South until the latitude of the destination was reached, and the ship would then sail East or West along the rhumb-line, maintaining a constant latitude and recording regular estimates of the distance sailed until evidence of land was sighted.
mathematician
Pedro Nunes
in 1537, in his Treatise in Defense of the Marine Chart, with further mathematical development by Thomas Harriot
in the 1590s.
A rhumb line can be contrasted with a great circle
, which is the shortest distance between two points on the surface of a sphere, but whose bearing is non-constant. If you were to drive a car along a great circle you would hold the steering wheel in the centre, but to follow a rhumb line you would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature
, whereas a rhumb line has non-zero geodesic curvature.
Meridians of longitude and parallels of latitude provide special cases of the rhumb line, where their angles of intersection are respectively 0° and 90°. On a North-South passage the rhumb-line course coincides with a great circle, as it does on an East-West passage along the equator.
On a Mercator projection
map, a rhumb line is a straight line; a rhumb line can be drawn on such a map between any two points on Earth without going off the edge of the map. But theoretically a loxodrome can extend beyond the right edge of the map, where it then continues at the left edge with the same slope (assuming that the map covers exactly 360 degrees of longitude).
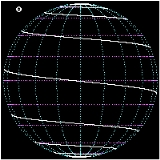
Rhumb lines which cut meridians at oblique angles are loxodromic curves which spiral towards the poles. On a Mercator projection the North and South poles occur at infinity and are therefore never shown. However the full loxodrome on an infinitely high map would consist of infinitely many line segments between the two edges. On a stereographic projection
map, a loxodrome is an equiangular spiral whose center is the North (or South) Pole.
All loxodromes spiral from one pole
to the other. Near the poles, they are close to being logarithmic spiral
s (on a stereographic projection
they are exactly, see below), so they wind round each pole an infinite number of times but reach the pole in a finite distance. The pole-to-pole length of a loxodrome is (assuming a perfect sphere
) the length of the meridian
divided by the cosine of the bearing away from true north. Loxodromes are not defined at the poles.
from true north of the loxodrome and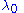
be the longitude where the loxodrome passes the equator. Let 
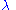be the longitude of a point on the loxodrome. Under the Mercator projection
the loxodrome will be a straight line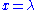
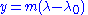
with slope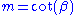
. For a point with latitude 
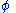and longitude 
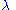the position in the Mercator projection can be expressed as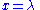
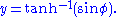
Then the latitude of the point will be
or in terms of the Gudermannian function gd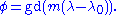
In cartesian coordinates this can be simplified to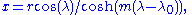
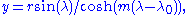
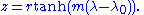
Finding the loxodromes between two given points can be done graphically on a Mercator map, or by solving a nonlinear system of two equations in the two unknowns tan(α) and λ0. There are infinitely many solutions; the shortest one is that which covers the actual longitude difference, i.e. does not make extra revolutions, and does not go "the wrong way around".
The distance between two points, measured along a loxodrome, is simply the absolute value of the secant
of the bearing (azimuth) times the north-south distance (except for circles of latitude for which the distance becomes infinite).
The above formulas assume a spherical earth; the formulas for the spheroid are of course more complicated, but not hopelessly so.
.
The 1878 edition ofThe Globe Encyclopaedia of Universal Information describes loxodrome lines as:
, that is, as a projection of the sphere to the complex plane
. In this case, loxodromes can be understood as certain classes of Möbius transformations.
Note: this article incorporates text from the 1878 edition of The Globe Encyclopaedia of Universal Information, a work in the public domain
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, a rhumb line (or loxodrome) is a line crossing all meridians
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
of longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
at the same angle, i.e. a path derived from a defined initial bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
. That is, upon taking an initial bearing, one proceeds along the same bearing, without changing the direction as measured relative to true north
True north
True north is the direction along the earth's surface towards the geographic North Pole.True geodetic north usually differs from magnetic north , and from grid north...
.
Usage
Its use in navigation is directly linked to the style, or projectionMap projection
A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...
of certain navigational maps. A rhumb line appears as a straight line on a Mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
map.
The name is derived from Old French: "rumb", a line on the chart which intersects all meridians at the same angle. On a plane surface this would be the shortest distance between two points. Over the Earth's surface at low latitudes or over short distances it can be used for plotting a vehicle, aircraft or ship's course. Over longer distances and/or at higher latitudes great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
routes provide the shortest distances. However the inconvenience of having to continuously change bearings while travelling a great circle route makes rhumb line navigation appealing in certain instances.
The point can be illustrated with an East-West passage over 90 degrees of longitude along the equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
, for which the great-circle and rhumb-line distances are the same at 5400 nautical miles (10,000.8 km). At 20 degrees North the great-circle distance is 4997 miles (8,041.9 km) while the rhumb-line distance is 5074 miles (8,165.8 km), about 1½ percent further. But at 60 degrees North the great circle distance is 2485 miles (3,999.2 km) while the rhumb-line is 2700 miles (4,345.2 km), a difference of 8½ percent. A more extreme case is the air route between New York and Hong Kong, for which the rhumb-line path is 9700 nautical miles (17,964.4 km). The great-circle route over the North Pole is 7000 nautical miles (12,964 km), or 5½ hours less flying time at a typical cruising speed
Cruise (flight)
Cruise is the level portion of aircraft travel where flight is most fuel efficient. It occurs between ascent and descent phases and is usually the majority of a journey. Technically, cruising consists of heading changes only at a constant airspeed and altitude...
.
Some old maps in the Mercator projection have grids composed of lines of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
but also show rhumb lines which are oriented directly towards North, at a right angle from the North, or at some angle from the North which is some simple rational fraction of a right angle. These rhumb lines would be drawn so that they would converge at certain points of the map: lines going in every direction would converge at each of these points. See compass rose
Compass rose
A compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
. Such maps would necessarily have been in the Mercator projection therefore not all old maps would have been capable of showing rhumb-line markings.
The radial oriented lines on a compass rose are also called rhumbs. The expression "sailing on a rhumb" was used in the 16th–19th centuries to indicate a particular compass heading.
Some Muslim groups in North America face along the rhumb line to Mecca (southeastwards) as their qibla
Qibla
The Qiblah , also transliterated as Qibla, Kiblah or Kibla, is the direction that should be faced when a Muslim prays during salah...
(praying direction) instead of the most direct Great Circle path, which is northeastward from North America.
Early navigators in the time before the invention of the chronometer used rhumb-line courses on long ocean passages, because the ship's latitude could be established accurately by sightings of the Sun or stars but there was no accurate way to determine the longitude. The ship would sail North or South until the latitude of the destination was reached, and the ship would then sail East or West along the rhumb-line, maintaining a constant latitude and recording regular estimates of the distance sailed until evidence of land was sighted.
General and mathematical description
The effect of following a rhumb line course on the surface of a globe was first discussed by the PortuguesePortuguese people
The Portuguese are a nation and ethnic group native to the country of Portugal, in the west of the Iberian peninsula of south-west Europe. Their language is Portuguese, and Roman Catholicism is the predominant religion....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Pedro Nunes
Pedro Nunes
Pedro Nunes , was a Portuguese mathematician, cosmographer, and professor, from a New Christian family. Nunes, considered to be one of the greatest mathematicians of his time , is best known for his contributions in the technical field of navigation, which was crucial to the Portuguese period of...
in 1537, in his Treatise in Defense of the Marine Chart, with further mathematical development by Thomas Harriot
Thomas Harriot
Thomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland...
in the 1590s.
A rhumb line can be contrasted with a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
, which is the shortest distance between two points on the surface of a sphere, but whose bearing is non-constant. If you were to drive a car along a great circle you would hold the steering wheel in the centre, but to follow a rhumb line you would have to turn the wheel, turning it more sharply as the poles are approached. In other words, a great circle is locally "straight" with zero geodesic curvature
Geodesic curvature
In Riemannian geometry, the geodesic curvature k_g of a curve lying on a submanifold of the ambient space measures how far the curve is from being a geodesic...
, whereas a rhumb line has non-zero geodesic curvature.
Meridians of longitude and parallels of latitude provide special cases of the rhumb line, where their angles of intersection are respectively 0° and 90°. On a North-South passage the rhumb-line course coincides with a great circle, as it does on an East-West passage along the equator.
On a Mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
map, a rhumb line is a straight line; a rhumb line can be drawn on such a map between any two points on Earth without going off the edge of the map. But theoretically a loxodrome can extend beyond the right edge of the map, where it then continues at the left edge with the same slope (assuming that the map covers exactly 360 degrees of longitude).
Rhumb lines which cut meridians at oblique angles are loxodromic curves which spiral towards the poles. On a Mercator projection the North and South poles occur at infinity and are therefore never shown. However the full loxodrome on an infinitely high map would consist of infinitely many line segments between the two edges. On a stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
map, a loxodrome is an equiangular spiral whose center is the North (or South) Pole.
All loxodromes spiral from one pole
Geographical pole
A geographical pole is either of the two points—the north pole and the south pole—on the surface of a rotating planet where the axis of rotation meets the surface of the body...
to the other. Near the poles, they are close to being logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
s (on a stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
they are exactly, see below), so they wind round each pole an infinite number of times but reach the pole in a finite distance. The pole-to-pole length of a loxodrome is (assuming a perfect sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
) the length of the meridian
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
divided by the cosine of the bearing away from true north. Loxodromes are not defined at the poles.
Mathematical derivation
Let β be the constant bearingBearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
from true north of the loxodrome and
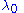be the longitude where the loxodrome passes the equator. Let 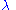be the longitude of a point on the loxodrome. Under the Mercator projectionMercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
the loxodrome will be a straight line
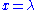
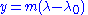
with slope
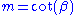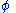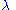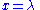
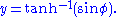
. For a point with latitude and longitude the position in the Mercator projection can be expressed asThen the latitude of the point will be
or in terms of the Gudermannian function gd
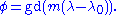
In cartesian coordinates this can be simplified to
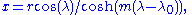
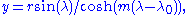
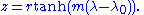
Finding the loxodromes between two given points can be done graphically on a Mercator map, or by solving a nonlinear system of two equations in the two unknowns tan(α) and λ0. There are infinitely many solutions; the shortest one is that which covers the actual longitude difference, i.e. does not make extra revolutions, and does not go "the wrong way around".
The distance between two points, measured along a loxodrome, is simply the absolute value of the secant
Secant
Secant is a term in mathematics. It comes from the Latin secare . It can refer to:* a secant line, in geometry* the secant variety, in algebraic geometry...
of the bearing (azimuth) times the north-south distance (except for circles of latitude for which the distance becomes infinite).
The above formulas assume a spherical earth; the formulas for the spheroid are of course more complicated, but not hopelessly so.
Etymology and historical description
The word "loxodrome" comes from Greek loxos : oblique + dromos : running (from dramein : to run). The word "rhumb" may come from Spanish/Portuguese rumbo/rumo (course, direction) and Greek ῥόμβοςRhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
.
The 1878 edition ofThe Globe Encyclopaedia of Universal Information describes loxodrome lines as:
- Loxodrom'ic Line is a curve which cuts every member of a system of lines of curvature of a given surface at the same angle. A ship sailing towards the same point of the compass describes such a line which cuts all the meridians at the same angle. In Mercator's Projection (q.v.) the Loxodromic lines are evidently straight.
On the Riemann sphere
The surface of the earth can be understood mathematically as a Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, that is, as a projection of the sphere to the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. In this case, loxodromes can be understood as certain classes of Möbius transformations.
External links
- Loxodromes: A Rhumb Way to Go (PDF)
- Constant Headings and Rhumb Lines at MathPages
- An example of a 16th-century Mercator projection with rhumb-lines
Note: this article incorporates text from the 1878 edition of The Globe Encyclopaedia of Universal Information, a work in the public domain