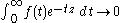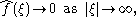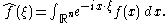Riemann-Lebesgue lemma
Encyclopedia
In mathematics
, the Riemann–Lebesgue lemma, named after Bernhard Riemann
and Henri Lebesgue
, is of importance in harmonic analysis
and asymptotic analysis
.
The lemma says that the Fourier transform
or Laplace transform of an L1 function
vanishes at infinity.
. If ƒ is L1 integrable
, that is to say if the Lebesgue integral of |ƒ| is finite, then

This says that the Fourier transform of ƒ tends to 0 as z tends to infinity.
Step 1. An elementary calculation shows that
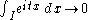 as
as 
for every interval I ⊂ [a, b]. The proposition is therefore true for all step functions with support in [a, b] (similarly, the proposition is also true for a slightly larger class of functions known as simple function
).
Step 2. By the dominated convergence theorem
, the proposition is true for all positive functions, integrable on [a, b].
Step 3. Let f be an arbitrary measurable function, integrable on [a, b]. The proposition is true for such a general f, because one can always write f = g − h where g and h are positive functions, integrable on [a, b].
Step 4. Because functions with compact support are dense in
L1(R),
this special case extends to the general result if we require t to be real.
The case of non-real t.
Assume first that f has a compact support on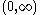 and that f is continuously differentiable.
and that f is continuously differentiable.
Denote the Fourier/Laplace transforms of f and by F and G, respectively.
by F and G, respectively.
Then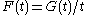 , hence
, hence 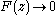 as
as 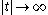 .
.
Because the functions of this form are dense in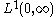 , the same holds for every f.
, the same holds for every f.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemann–Lebesgue lemma, named after Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
, is of importance in harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and asymptotic analysis
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
.
The lemma says that the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or Laplace transform of an L1 function
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
vanishes at infinity.
Statement
Let ƒ:R → C be a measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
. If ƒ is L1 integrable
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, that is to say if the Lebesgue integral of |ƒ| is finite, then

This says that the Fourier transform of ƒ tends to 0 as z tends to infinity.
Other versions
The Riemann–Lebesgue lemma holds in a variety of other situations.- If ƒ is L1 integrable and supported on (0, ∞), then the Riemann–Lebesgue lemma also holds for the Laplace transform of ƒ. That is,
-
- as |z| → ∞ within the half-plane Im(z) ≥ 0.
- A version holds for Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
as well: if ƒ is an integrable function on an interval, then the Fourier coefficients of ƒ tend to 0 as n → ±∞,
-
- This follows by extending ƒ by zero outside the interval, and then applying the version of the lemma on the entire real line.
- The lemma also holds for the Fourier transform in higher dimensions. If ƒ ∈ L1(Rn), then
-
- where
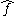 is the Fourier transform
is the Fourier transform
Applications
The Riemann–Lebesgue lemma can be used to prove the validity of asymptotic approximations for integrals. Rigorous treatments of the method of steepest descent and the method of stationary phase, amongst others, are based on the Riemann–Lebesgue lemma.Proof
The proof of the last special case can be organized into 3 steps; the 4th step extends the result to the first special case.Step 1. An elementary calculation shows that
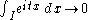 as
as 
for every interval I ⊂ [a, b]. The proposition is therefore true for all step functions with support in [a, b] (similarly, the proposition is also true for a slightly larger class of functions known as simple function
Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...
).
Step 2. By the dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
, the proposition is true for all positive functions, integrable on [a, b].
Step 3. Let f be an arbitrary measurable function, integrable on [a, b]. The proposition is true for such a general f, because one can always write f = g − h where g and h are positive functions, integrable on [a, b].
Step 4. Because functions with compact support are dense in
L1(R),
this special case extends to the general result if we require t to be real.
The case of non-real t.
Assume first that f has a compact support on
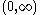 and that f is continuously differentiable.
and that f is continuously differentiable.Denote the Fourier/Laplace transforms of f and
 by F and G, respectively.
by F and G, respectively.Then
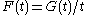 , hence
, hence 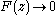 as
as 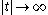 .
.Because the functions of this form are dense in
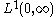 , the same holds for every f.
, the same holds for every f.