Riemann problem - AbsoluteAstronomy.com

A Riemann problem, named after Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

, consists of a conservation law

Conservation law

In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....

together with piecewise

Piecewise

On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...

constant data having a single discontinuity

Discontinuity

Discontinuity may refer to:*Discontinuity , a harmless irregularity in a casting*Discontinuity in geotechnics is a plane or surface marking a change in physical or chemical properties in a soil or rock mass...

. The Riemann problem
is very useful for the understanding of hyperbolic partial differential equation

Hyperbolic partial differential equation

In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...

s like the Euler equations because all properties, such as shocks and rarefaction waves, appear as characteristic

Method of characteristics

In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...

s in the solution. It also gives an exact solution to some complex nonlinear equations, such as the Euler equations.

In numerical analysis

Numerical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

, Riemann problems appear in a natural way in finite volume method

Finite volume method

The finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]....

s for the solution of equation of conservation laws due to the discreteness of the grid. For that it is widely used in computational fluid dynamics

Computational fluid dynamics

Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...

and in MHD

Computational Magnetohydrodynamics

Computational magnetohydrodynamics is a rapidly developing branch of magnetohydrodynamics that uses numerical methods and algorithms to solve and analyze problems that involve electrically conducting fluids. Most of the methods used in CMHD are borrowed from the well established techniques...

simulations. In these fields Riemann problems are calculated using Riemann solver

Riemann solver

A Riemann solver is a numerical method used to solve a Riemann problem. They are heavily used in computational fluid dynamics and computational magnetohydrodynamics.-Exact solvers:...

The Riemann problem in linearized gas dynamics

As a simple example, we investigate the properties of the one dimensional Riemann problem
in gas dynamics

Gas dynamics

Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics...

, which is defined by

where x = 0 separates two different states, together with the linearised gas dynamic equation (see gas dynamics

Gas dynamics

Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics...

for derivation)

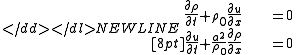
we can rewrite the above equation in conservative form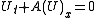

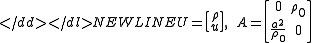
The eigenvalues of the system are the characteristics of the system

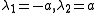. They give the propagation speed of the medium, including that of any discontinuity, which is the speed of sound here. The corresponding eigenvectors are

By decomposing the left state

in terms of the eigenvectors, we get

Now we can solve for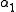

and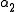

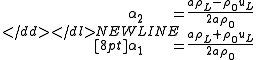
By doing the same for the right state we get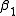

and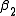

. Which is

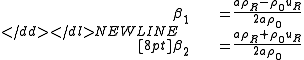
With this, we get the final solution in the domain in between the characteristics, which is

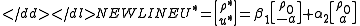
As this just a simple example, it still shows the basic properties. Most important the characteristics which decompose the solution into three domains. The propagation speed
of these two equations is equivalent to the propagations speed of the sound.

The fastest characteristic defines the CFL

Courant–Friedrichs–Lewy condition

In mathematics, the Courant–Friedrichs–Lewy condition is a necessary condition for convergence while solving certain partial differential equations numerically by the method of finite differences. It arises when explicit time-marching schemes are used for the numerical solution...

condition, which sets the restriction for the maximum time step in a computer simulation. Generally as more conservation equations are used, the more characteristics are involved.

The Riemann problem in linearized gas dynamics

See also