
Riesz transform
Encyclopedia
In the mathematical
theory of harmonic analysis
, the Riesz transforms are a family of generalizations of the Hilbert transform
to Euclidean space
s of dimension d > 1. They are a type of singular integral operator, meaning that they are given by a convolution
of one function with another function having a singularity at the origin. Specifically, the Riesz transforms of a complex-valued function ƒ on Rd are defined by
for j = 1,2,...,d. The constant cd is a dimensional normalization given by
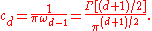
where ωd−1 is the volume of the (d − 1)-ball. The limit is written in various ways, often as a principal value
, or as a convolution
with the tempered distribution

The Riesz transforms arises in the study of differentiability properties of harmonic potentials in potential theory
and harmonic analysis
. In particular, they arise in the proof of the Calderón-Zygmund inequality .
of Rjƒ is given by
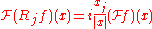
(up to an overall positive constant depending on the normalization of the Fourier transform). In this form, the Riesz transforms are seen to be generalizations of the Hilbert transform. The kernel is a distribution
which is homogeneous
of degree zero. A particular consequence of this last observation is that the Riesz transform defines a bounded linear operator from L2(Rd) to itself.
This homogeneity property can also be stated more directly without the aid of the Fourier transform. If σs is the dilation on Rd by the scalar s, that is σsx = sx, then σs defines an action on functions via pullback:

The Riesz transforms commute with σs:
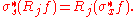
Similarly, the Riesz transforms commute with translations. Let τa be the translation on Rd along the vector a; that is, τa(x) = x + a. Then
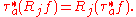
For the final property, it is convenient to regard the Riesz transforms as a single vectorial entity Rƒ = (R1ƒ,…,Rdƒ). Consider a rotation
ρ in Rd. The rotation acts on spatial variables, and thus on functions via pullback. But it also can act on the spatial vector Rƒ. The final transformation property asserts that the Riesz transform is equivariant
with respect to these two actions; that is,

These three properties in fact characterize the Riesz transform in the following sense. Let T=(T1,…,Td) be a d-tuple of bounded linear operators from L2(Rd) to L2(Rd) such that
Then, for some constant c, T = cR.
s of a solution of the equation
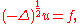
where Δ is the Laplacian. Thus the Riesz transform of ƒ can be written as:

In particular, one should also have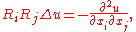
so that the Riesz transforms give a way of recovering information about the entire hessian
of a function from knowledge of only its Laplacian.
This is now made more precise. Suppose that u is a Schwartz function. Then indeed by the explicit form of the Fourier multiplier, one has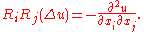
The identity is not generally true in the sense of distributions
. For instance, if u is a tempered distribution
such that Δu ∈ L2(Rd), then one can only conclude that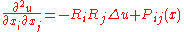
for some polynomial Pij.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, the Riesz transforms are a family of generalizations of the Hilbert transform
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s of dimension d > 1. They are a type of singular integral operator, meaning that they are given by a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of one function with another function having a singularity at the origin. Specifically, the Riesz transforms of a complex-valued function ƒ on Rd are defined by
for j = 1,2,...,d. The constant cd is a dimensional normalization given by
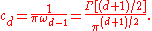
where ωd−1 is the volume of the (d − 1)-ball. The limit is written in various ways, often as a principal value
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
, or as a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with the tempered distribution
Tempered distribution
*Distribution *Tempered representation...

The Riesz transforms arises in the study of differentiability properties of harmonic potentials in potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. In particular, they arise in the proof of the Calderón-Zygmund inequality .
Multiplier properties
The Riesz transform are given by a Fourier multiplier. Indeed, the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of Rjƒ is given by
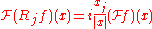
(up to an overall positive constant depending on the normalization of the Fourier transform). In this form, the Riesz transforms are seen to be generalizations of the Hilbert transform. The kernel is a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
which is homogeneous
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree zero. A particular consequence of this last observation is that the Riesz transform defines a bounded linear operator from L2(Rd) to itself.
This homogeneity property can also be stated more directly without the aid of the Fourier transform. If σs is the dilation on Rd by the scalar s, that is σsx = sx, then σs defines an action on functions via pullback:

The Riesz transforms commute with σs:
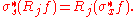
Similarly, the Riesz transforms commute with translations. Let τa be the translation on Rd along the vector a; that is, τa(x) = x + a. Then
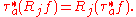
For the final property, it is convenient to regard the Riesz transforms as a single vectorial entity Rƒ = (R1ƒ,…,Rdƒ). Consider a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
ρ in Rd. The rotation acts on spatial variables, and thus on functions via pullback. But it also can act on the spatial vector Rƒ. The final transformation property asserts that the Riesz transform is equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
with respect to these two actions; that is,

These three properties in fact characterize the Riesz transform in the following sense. Let T=(T1,…,Td) be a d-tuple of bounded linear operators from L2(Rd) to L2(Rd) such that
- T commutes with all dilations and translations.
- T is equivariant with respect to rotations.
Then, for some constant c, T = cR.
Relationship with the Laplacian
Somewhat imprecisely, the Riesz transforms of ƒ give the first partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of a solution of the equation
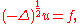
where Δ is the Laplacian. Thus the Riesz transform of ƒ can be written as:

In particular, one should also have
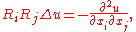
so that the Riesz transforms give a way of recovering information about the entire hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of a function from knowledge of only its Laplacian.
This is now made more precise. Suppose that u is a Schwartz function. Then indeed by the explicit form of the Fourier multiplier, one has
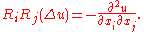
The identity is not generally true in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. For instance, if u is a tempered distribution
Tempered distribution
*Distribution *Tempered representation...
such that Δu ∈ L2(Rd), then one can only conclude that
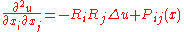
for some polynomial Pij.

