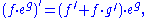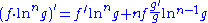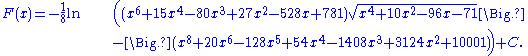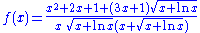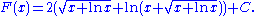Risch algorithm
Encyclopedia
The Risch algorithm, named after Robert Henry Risch, is an algorithm
for the calculus
operation of indefinite integration (i.e., finding antiderivative
s). The algorithm transforms the problem of integration into a problem in algebra
. It is based on the form of the function being integrated and on methods for integrating rational function
s, radical
s, logarithm
s, and exponential function
s. Risch, who developed the algorithm in 1968, called it a decision procedure, because it is a method for deciding if a function has an elementary function
as an indefinite integral; and also, if it does, determining it. The Risch algorithm is summarized (in more than 100 pages) in Algorithms for Computer Algebra by Keith O. Geddes
, Stephen R. Czapor and George Labahn. The Risch–Norman algorithm (after A. C. Norman), a faster but less powerful technique, was developed in 1976.
solved this problem for the case of rational functions, as he showed that the indefinite integral of a rational function is a rational function and a finite number of constant multiples of logarithms of rational functions. The algorithm suggested by Laplace is usually described in calculus textbooks; as a computer program it was finally implemented in the 1960s.
Liouville
formulated the problem solved by the Risch algorithm. Liouville proved by analytical means that if there is an elementary solution g to the equation g ′ = f then for constants αi and elementary functions ui and v the solution is of the form
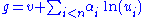
Risch developed a method that allows one to only consider a finite set of elementary functions of Liouville's form.
The intuition for the Risch algorithm comes from the behavior of the exponential and logarithm functions under differentiation. For the function f eg, where f and g are differentiable function
s, we have
so if eg were in the result of an indefinite integration, it should be expected to be inside the integral. Also, as
then if lnng were in the result of an integration, then only a few powers of the logarithm should be expected.
namely:
(Some computer algebra systems may here return an antiderivative in terms of non-elementary functions (i.e. elliptic integral
s), which however are outside the scope of the Risch algorithm.) But if 71 is changed to 72, it is not possible to represent the antiderivative using elementary functions. The reason is that the Galois group
of
is D(4), e.g. generated by permutations (1 2 3 4) and (1 3), and contains 8 elements (same as in x4 − 2), while the Galois group of
is S(4), e.g. generated by permutations (1 2), (1 3), (1 4), and contains 24 elements.
The following function is a more complex example:
In fact, the antiderivative of this function has a fairly short form:
s have partial implementations.
because it needs to check, as a part of its operation, if certain expressions are equivalent to zero (constant problem
), in particular in the constant field. For expressions that involve only functions commonly taken to be elementary it is not known whether an algorithm performing such a check exists or not (current computer algebra system
s use heuristics); moreover, if one adds the absolute value function
to the list of elementary functions, it is known that no such algorithm exists; see Richardson's theorem
.
Note that this issue also arises in the polynomial division algorithm; this algorithm will fail if it cannot correctly determine whether coefficients vanish identically. Therefore, the Risch algorithm too requires that the constant field be computable, i.e., that for elements not dependent on x, the problem of zero-equivalence is decidable.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for the calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
operation of indefinite integration (i.e., finding antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s). The algorithm transforms the problem of integration into a problem in algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
. It is based on the form of the function being integrated and on methods for integrating rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s, radical
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s, and exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s. Risch, who developed the algorithm in 1968, called it a decision procedure, because it is a method for deciding if a function has an elementary function
Elementary function (differential algebra)
In mathematics, an elementary function is a function of one variable built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations...
as an indefinite integral; and also, if it does, determining it. The Risch algorithm is summarized (in more than 100 pages) in Algorithms for Computer Algebra by Keith O. Geddes
Keith Geddes
Keith Geddes is a professor emeritus in the David R. Cheriton School of Computer Science within the Faculty of Mathematics at the University of Waterloo in Waterloo, Ontario. He is a former director of the in the School of Computer Science...
, Stephen R. Czapor and George Labahn. The Risch–Norman algorithm (after A. C. Norman), a faster but less powerful technique, was developed in 1976.
Description
The Risch algorithm is used to integrate elementary functions. These are functions obtained by composing exponentials, logarithms, radicals, trigonometry, and the four arithmetic operations (+ − × ÷). LaplacePierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
solved this problem for the case of rational functions, as he showed that the indefinite integral of a rational function is a rational function and a finite number of constant multiples of logarithms of rational functions. The algorithm suggested by Laplace is usually described in calculus textbooks; as a computer program it was finally implemented in the 1960s.
Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
formulated the problem solved by the Risch algorithm. Liouville proved by analytical means that if there is an elementary solution g to the equation g ′ = f then for constants αi and elementary functions ui and v the solution is of the form
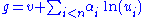
Risch developed a method that allows one to only consider a finite set of elementary functions of Liouville's form.
The intuition for the Risch algorithm comes from the behavior of the exponential and logarithm functions under differentiation. For the function f eg, where f and g are differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s, we have
so if eg were in the result of an indefinite integration, it should be expected to be inside the integral. Also, as
then if lnng were in the result of an integration, then only a few powers of the logarithm should be expected.
Problem examples
Finding an elementary antiderivative is very sensitive to details. For instance, the following function has an elementary antiderivative:namely:
(Some computer algebra systems may here return an antiderivative in terms of non-elementary functions (i.e. elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s), which however are outside the scope of the Risch algorithm.) But if 71 is changed to 72, it is not possible to represent the antiderivative using elementary functions. The reason is that the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of
is D(4), e.g. generated by permutations (1 2 3 4) and (1 3), and contains 8 elements (same as in x4 − 2), while the Galois group of
is S(4), e.g. generated by permutations (1 2), (1 3), (1 4), and contains 24 elements.
The following function is a more complex example:
In fact, the antiderivative of this function has a fairly short form:
Implementation
Transforming the Risch decision procedure into an algorithm that can be executed by a computer is a complex task that requires the use of heuristics and many refinements. No software is known to implement the full Risch algorithm, although several computer algebra systemComputer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s have partial implementations.
Decidability
The Risch algorithm applied to general elementary functions is not an algorithm but a semi-algorithmRE (complexity)
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to...
because it needs to check, as a part of its operation, if certain expressions are equivalent to zero (constant problem
Constant problem
In mathematics, the constant problem is the problem of deciding if a given expression is equal to zero.-The problem:This problem is also referred to as the identity problem or the method of zero estimates. It has no formal statement as such but refers to a general problem prevalent in...
), in particular in the constant field. For expressions that involve only functions commonly taken to be elementary it is not known whether an algorithm performing such a check exists or not (current computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s use heuristics); moreover, if one adds the absolute value function
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
to the list of elementary functions, it is known that no such algorithm exists; see Richardson's theorem
Richardson's theorem
In mathematics, Richardson's theorem establishes a limit on the extent to which an algorithm can decide whether certain mathematical expressions are equal...
.
Note that this issue also arises in the polynomial division algorithm; this algorithm will fail if it cannot correctly determine whether coefficients vanish identically. Therefore, the Risch algorithm too requires that the constant field be computable, i.e., that for elements not dependent on x, the problem of zero-equivalence is decidable.
See also
- Lists of integrals
- Liouville's theorem (differential algebra)Liouville's theorem (differential algebra)In mathematics, Liouville's theorem, originally formulated by Joseph Liouville in the 1830s and 1840s, places an important restriction on antiderivatives that can be expressed as elementary functions....
- Symbolic integrationSymbolic integrationIn calculus symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f, i.e...
- Axiom (computer algebra system)
- Incomplete Gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...