Rod calculus
Encyclopedia
Rod calculus or rod calculation is the method of mathematical computation with counting rods
in China from the Warring States to Ming dynasty
before the counting rods were replaced by the more convenient and faster abacus
.
and a counting board. The counting rods are usually made of bamboo sticks, about 12 cm- 15cm in length, 2mm to 4 mm diameter, sometimes from animal bones, or ivory and jade (for well heeled merchants). A counting board could be a table top, a wooden board with or without grid, on the floor or on sand.
In 1971 Chinese archeologists unearthed a bundle of well preserved animal bone counting rods stored in a silk pouch from a tomb in Qian Yang county in Shanxi province, dated back to the first half of Han dynasty
(206 BC - 8AD). In 1975 a bundle of bamboo counting rods was unearthed.
The use of counting rods for rod calculus flourished in the Warring States, although no archeological artifacts were found earlier than the Western Han Dynasty(the first half of Han dynasty
, however archeologist did unearth software artifacts of rod calculus dated back to the Warring States); since the rod calculus software must have gone along with rod calculus hardware, there is no doubt that rod calculus was already flourishing during the Warring States more than 2,200 years ago.
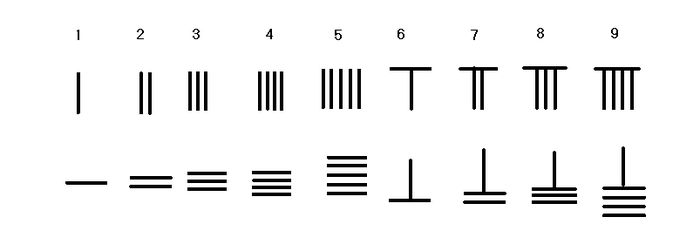
Rod Numerals is the only numeric system that uses different placement of a single symbol to convey any number or fraction in the Decimal System. For numbers in the units place, every vertical rod represent 1. Two vertical rods represent 2, and so on, until 5 vertical rods, which represents 5. For number between 6 and 9, a biquinary system is used, in which a horizontal bar on top of the vertical bars represent 5. The first row are the number 1 to 9 in rod numerals, and the second row is the same numbers in horizontal form.
For numbers larger than 9, a decimal system
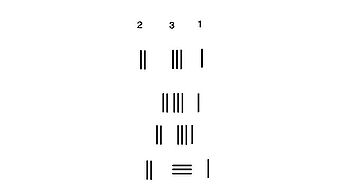
is used. Rods placed one place to the left of the units place represent 10 times that number. For the hundreds place, another set of rods is placed to the left which represents 100 times of that number, and so on. As shown in the image to the right, the number 231 is represented in rod numerals in the top row, with one rod in the units place representing 1, three rods in the tens place representing 30, and two rods in the hundreds place representing 200, with a sum of 231.
When doing calculation, usually there was no grid on the surface. If rod numerals two, three, and one is placed consecutively in the vertical form, there's a possibility of it being mistaken for 51 or 24, as shown in the second and third row of the image to the right. To avoid confusion, number in consecutive places are placed in alternating vertical and horizontal form, with the units place in vertical form, as shown in the bottom row on the right.
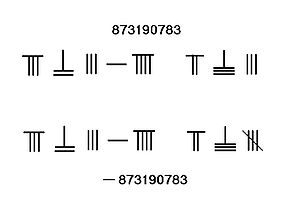
, zeroes are represented by a space, which serves both as a number and a place holder value. Unlike in Arabic Numerals
, there is no specific symbol to represent zero. In the image to the right, the number zero is merely represented with a space.
mathematicians used red to represent positive numbers and black for negative numbers. However, another way is to add a slash to the last place to show that the number is negative.
1 chi=10cun,1cun=10fen,1fen=10li,1li=10hao,1hou=10hu.
1 chi2cun3fen4li5hao6shi7hu is laid out on counting board as
where
is the unit measurement chi.
Southern Song dynasty mathematicial Qin Jiushao extended the use of decimal fraction beyond metrology. In his book Shu shu Jiuzhang
he formally expressed 1.1446154 day as
He marked the unit with a word “日”(day) underneath it。
, counting rods itself have additive properties. The process of addition involves mechanically moving the rods without the need of memorizing an addition table. This is the biggest difference with Arabic Numerals, as one cannot mechanically put 1 and 2 together to form 3, or 2 and 3 together to form 5.
The image to the right presents the steps in adding 3748 to 289:
The rods in the augend changes throughout the addition, while the rods in the addend at the bottom "disappears".
Augend's rods in the first row changes throughout the addition. Addend's rods in the bottom "disappears" throughout the process.
described in detail the algorithm of multiplication in The Mathematical Classic of Sun Zi
. On the right are the steps to calculate 38×76:
The animation on the left shows the steps for calculating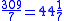
The Sunzi algorithm for division was transmitted in toto by al Khwarizmi to Islamic country from Indian sources in 825AD. Al Khwarizmi's book was translated into Latin in 13th century, The Sunzi division algorithm later evolved into Galley division
in Europe. The division algorithm in Abu'l-Hasan al-Uqlidisi
's 925AD book Kitab al-Fusul fi al-Hisab al-Hindi and in 11th century Kushyar ibn Labban
's Principles of Hindu Reckoning
were identical to Sunzu's division algorithm.
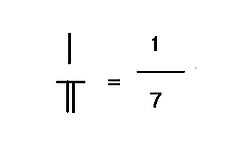
's notes to Jiuzhang suanshu (2nd century BCE), the number on top is called "shi实", while the one at bottom is called "fa法". In Sun Tzu
's Calculation Classic, the number on top is called "zi子" or "fenzi" (lit., son of fraction), and the one on the bottom is called "mu母" or "fenmu" (lit., mother of fraction). Fenzi and Fenmu are also the modern Chinese name for numerator and denominator, respectively. As shown on the right, 1 is the numerator remainder, 7 is the denominator divisor, formed a fraction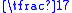
. The quotient of the division 309/7 is 44 + 
.
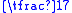Liu Hui's used a lot of calculations with fraction in The Sea Island Mathematical Manual
.
This form of fraction with numerator on top and denominator at bottom without a horizontal bar in between, was transmitted to Arabic country in a 825AD book by al Khwarizmi via India, and in use by 10th century Abu'l-Hasan al-Uqlidisi
and 15th century Jamshīd al-Kāshī
's work "Arithematic Key".
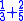
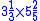
fraction was laid out in Jiuzhang suanshu.
The highest common factor is found by successive division with remainders until
the last two remainders are identical.
The animation on the right illustrates the algorithm for finding the hightest common factor of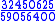
and reduction of a fraction.
In this case the hcf is 25.
Divide the numerator and denominator by 25.The reduced fraction is
.
's legendary π=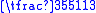
could be obtained with He Chengtian's method
Problem 8-1: Suppose we have 3 bundles of top quality cereals, 2 bundles of medium quality cereals and a bundle of low quality cereal, total thirty nine dou. We also have 2, 3 bundles and 1 bundle of respective cereals amount to 34 dou; we also have 1,2 and 3 bundles of respective cereals, total 26 dou.
Find the quantity of top, medium, and poor quality cereals.
In algebra, this problem can be expressed in three system equation with three unknowns.
This problem was solved in Jiuzhang suanshu with counting rods laid out on counting board in a tabular format similar to a 3x4 matrix:
Algorithm:
The amount of on bundle of low quality cereal =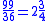
From which the amount of one bundle of top and medium quality cereals can be found easily:
One bundle of top quality cereals=9 dou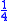
One bundle of medium cereal=4 dou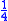
>
.
The animation shows the algorithm for rod calculus extraction of an approximation of the square root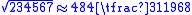
from the algorithm in chap 2 problem 19 of The Mathematical Classic of Sun Zi:
The algorithm is as follows:
.
North Song dynasty mathematician Jia Xian
developed addtive multiplicative algorithm for extration square root, in which he replaced the traditional "doubling" of "fang fa" by adding
shang digit to fang fa digit, with same effect.
〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何？答曰：一百二十三尺。
problem 19: We have a 1860867 cubic chi, what is the length of a side ? Answer:123 chi.
North Song dynasty mathematician Jia Xian
invented a method similar to simplified form of Horner scheme
for extraction of cubic root.
The animation at right shows Jia Xian's algorithm for solving problem 19 in Jiuzhang suanshu vol 4.
invented Horner scheme
for solving simple 4th order equation of the form
South Song dynasty mathematician Qin Jiushao improved Jia Xian's Horner method to solve polynomial equation up to 10th order.
The following is algorithm for solving
This equation was arranged bottom up with counting rods on counting board in tabular form
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
in China from the Warring States to Ming dynasty
Ming Dynasty
The Ming Dynasty, also Empire of the Great Ming, was the ruling dynasty of China from 1368 to 1644, following the collapse of the Mongol-led Yuan Dynasty. The Ming, "one of the greatest eras of orderly government and social stability in human history", was the last dynasty in China ruled by ethnic...
before the counting rods were replaced by the more convenient and faster abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
.
Hardware
The basic equipment for carrying out rod calculus is a bundle of counting rodsCounting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
and a counting board. The counting rods are usually made of bamboo sticks, about 12 cm- 15cm in length, 2mm to 4 mm diameter, sometimes from animal bones, or ivory and jade (for well heeled merchants). A counting board could be a table top, a wooden board with or without grid, on the floor or on sand.
In 1971 Chinese archeologists unearthed a bundle of well preserved animal bone counting rods stored in a silk pouch from a tomb in Qian Yang county in Shanxi province, dated back to the first half of Han dynasty
Han Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
(206 BC - 8AD). In 1975 a bundle of bamboo counting rods was unearthed.
The use of counting rods for rod calculus flourished in the Warring States, although no archeological artifacts were found earlier than the Western Han Dynasty(the first half of Han dynasty
Han Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
, however archeologist did unearth software artifacts of rod calculus dated back to the Warring States); since the rod calculus software must have gone along with rod calculus hardware, there is no doubt that rod calculus was already flourishing during the Warring States more than 2,200 years ago.
Software
The key software required for rod calculus was a simple 45 phrase positional decimal multiplication table used in China since antiquity, called the nine-nine table, which were learned by heart by pupils, merchants, government officials and mathematicians alike.Displaying Numbers
For numbers larger than 9, a decimal system
Decimal system
Decimal system may refer to:* The decimal number system, used in mathematics for writing numbers and performing arithmetic.* The Dewey Decimal System, a subject classification system used in libraries....
is used. Rods placed one place to the left of the units place represent 10 times that number. For the hundreds place, another set of rods is placed to the left which represents 100 times of that number, and so on. As shown in the image to the right, the number 231 is represented in rod numerals in the top row, with one rod in the units place representing 1, three rods in the tens place representing 30, and two rods in the hundreds place representing 200, with a sum of 231.
When doing calculation, usually there was no grid on the surface. If rod numerals two, three, and one is placed consecutively in the vertical form, there's a possibility of it being mistaken for 51 or 24, as shown in the second and third row of the image to the right. To avoid confusion, number in consecutive places are placed in alternating vertical and horizontal form, with the units place in vertical form, as shown in the bottom row on the right.
Displaying Zeroes
In Rod NumeralsCounting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
, zeroes are represented by a space, which serves both as a number and a place holder value. Unlike in Arabic Numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
, there is no specific symbol to represent zero. In the image to the right, the number zero is merely represented with a space.
Negative and Positive Numbers
SongSong Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians used red to represent positive numbers and black for negative numbers. However, another way is to add a slash to the last place to show that the number is negative.
Decimal fraction
The Mathematical Treatise of Sun Zi used decimal fraction metrology. The unit of length was 1 chi,1 chi=10cun,1cun=10fen,1fen=10li,1li=10hao,1hou=10hu.
1 chi2cun3fen4li5hao6shi7hu is laid out on counting board as
where
is the unit measurement chi.Southern Song dynasty mathematicial Qin Jiushao extended the use of decimal fraction beyond metrology. In his book Shu shu Jiuzhang
he formally expressed 1.1446154 day as
-
-
-
-
-
- 日
-
-
-
-
He marked the unit with a word “日”(day) underneath it。
Addition
Rod calculus itself works on the principle of addition. Unlike Arabic NumeralsArabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
, counting rods itself have additive properties. The process of addition involves mechanically moving the rods without the need of memorizing an addition table. This is the biggest difference with Arabic Numerals, as one cannot mechanically put 1 and 2 together to form 3, or 2 and 3 together to form 5.
The image to the right presents the steps in adding 3748 to 289:
- Place the augend 3748 in the first row, and the addend 289 in the second.
- Calculate from LEFT to RIGHT, from the 2 of 289 first.
- Take away two rod from the bottom add to 7 on top to make 9.
- Move 2 rods from top to bottom 8 , carry one to forward to 9, which becomes zero and carries to 3 to make 4, remove 8 from bottom row.
- Move one rod from 8 on top row to 9 on bottom to form a carry one to next rank and add one rod to 2 rods on top row to make 3 rods, top row left 7.
- Result 3748+289=4037
The rods in the augend changes throughout the addition, while the rods in the addend at the bottom "disappears".
Augend's rods in the first row changes throughout the addition. Addend's rods in the bottom "disappears" throughout the process.
Without Borrowing
In situation in which no borrowing is needed, one only needs to take the number of rods in the subtrahend from the minuend. The result of the calculation is the difference. The image on the left shows the steps in subtracting 23 from 54.Borrowing
In situations in which borrowing is needed such as 4231-789, the steps are shown on the right.- Place the minuend 4231 on top, the subtrahend 789 on the bottom. Calculate from the left to the right.
- Borrow 1 from the thousands place for a ten in the hundreds place, minus 7 from the row below, the difference 3 is added to the 2 on top to form 5. The 7 on the bottom is subtracted, shown by the space.
- Borrow 1 from the hundreds place, which leaves 4. The 10 in the tens place minus the 8 below results in 2, which is added to the 3 above to form 5. The top row now is 3451, the bottom 9.
- Borrow 1 from the 5 in the tens place on top, which leaves 4. The 1 borrowed from the tens is 10 in the units place, subtracting 9 which results in 1, which are added to the top to form 2. With all rods in the bottom row subtracted, the 3442 in the top row is then, the result of the calculation
Multiplication
Sun TzuSun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
described in detail the algorithm of multiplication in The Mathematical Classic of Sun Zi
The Mathematical Classic of Sun Zi
The Mathematical Classic of Sun Zi was a mathematical treatise written during the 5th century, and was listed as one of The Ten Computational Canons in Tang Dynasty. The identity of the author Sunzi is still unknown, and not to be confused with the author of The Art of War...
. On the right are the steps to calculate 38×76:
- Place the multiplicand on top, the multiplier on bottom. Line up the units place of the multiplier with the highest place of the multiplicand. Leave room in the middle for recording.
- Start calculating from the highest place of the multiplicand (in the example, calculate 30×76, and then 8×76). Using the multiplication tableMultiplication tableIn mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
3 times 7 is 21. Place 21 in rods in the middle, with 1 aligned with the tens place of the multiplier (on top of 7). Then, 3 times 6 equals 18, place 18 as it is shown in the image. With the 3 in the multiplicand multiplied totally, take the rods off. - Move the multiplier one place to the right. Change 7 to horizontal form, 6 to vertical.
- 8×7 = 56, place 56 in the second row in the middle, with the units place aligned with the digits multiplied in the multiplier. Take 7 out of the multiplier since it has been multiplied.
- 8×6 = 48, 4 added to the 6 of the last step makes 10, carry 1 over. Take off 8 of the units place in the multiplicand, and take off 6 in the units place of the multiplier.
- Sum the 2380 and 508 in the middle, which results in 2888, the product.
Division
.The animation on the left shows the steps for calculating
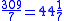
- Place the dividend, 309, in the middle row and the divisor, 7, in the bottom row. Leave space for the top row.
- Move the divisor, 7, one place to the left, changing it to horizontal form.
- Using the Chinese multiplication tableChinese multiplication tableThe Chinese multiplication table is the first requisite for using the Rod calculus for carrying out multiplication, division, the extraction of square roots, and the solving of equations based on place value decimal notation...
and division, 30÷7 equals 4 remainder 2. Place the quotient, 4, in the top row and the remainder, 2, in the middle row. - Move the divisor one place to the right, changing it to vertical form. 29÷7 equals 4 remainder 1. Place the quotient, 4, on top, leaving the divisor in place. Place the remainder in the middle row in place of the dividend in this step. The result is the quotient is 44 with a remainder of 1
The Sunzi algorithm for division was transmitted in toto by al Khwarizmi to Islamic country from Indian sources in 825AD. Al Khwarizmi's book was translated into Latin in 13th century, The Sunzi division algorithm later evolved into Galley division
Galley division
In arithmetic, the galley method, also known as the batello or the scratch method, was the most widely used method of division in use prior to 1600. The names galea and batello refer to a boat which the outline of the work was thought to resemble.An earlier version of this method was used as early...
in Europe. The division algorithm in Abu'l-Hasan al-Uqlidisi
Abu'l-Hasan al-Uqlidisi
Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
's 925AD book Kitab al-Fusul fi al-Hisab al-Hindi and in 11th century Kushyar ibn Labban
Kushyar ibn Labban
Abul-Hasan Kūshyār ibn Labbān ibn Bashahri Gilani , also known as Kūshyār Gīlānī , was a Persian mathematician, geographer, and astronomer from Gilan, south of the Caspian Sea, Iran....
's Principles of Hindu Reckoning
Principles of Hindu Reckoning
Principles of Hindu Reckoning is a mathematics book written by 10th–11th-century Persian mathematician Kushyar ibn Labban...
were identical to Sunzu's division algorithm.
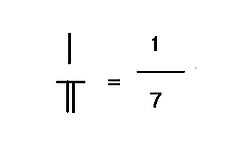
Fractions
If there is a remainder in a place value decimal rod calculus division, both the remainder and the divisor must be left in place with one on top of another. In Liu HuiLiu Hui
Liu Hui was a mathematician of the state of Cao Wei during the Three Kingdoms period of Chinese history. In 263, he edited and published a book with solutions to mathematical problems presented in the famous Chinese book of mathematic known as The Nine Chapters on the Mathematical Art .He was a...
's notes to Jiuzhang suanshu (2nd century BCE), the number on top is called "shi实", while the one at bottom is called "fa法". In Sun Tzu
Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
's Calculation Classic, the number on top is called "zi子" or "fenzi" (lit., son of fraction), and the one on the bottom is called "mu母" or "fenmu" (lit., mother of fraction). Fenzi and Fenmu are also the modern Chinese name for numerator and denominator, respectively. As shown on the right, 1 is the numerator remainder, 7 is the denominator divisor, formed a fraction
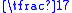. The quotient of the division 309/7 is 44 + 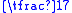.Liu Hui's used a lot of calculations with fraction in The Sea Island Mathematical Manual
The Sea Island Mathematical Manual
The Sea Island Mathematical Manual or Haidao suanjing was written by the Chinese mathematician Liu Hui of the Three Kingdoms era as an extension of chapter 9 of The Nine Chapters on the Mathematical Art....
.
This form of fraction with numerator on top and denominator at bottom without a horizontal bar in between, was transmitted to Arabic country in a 825AD book by al Khwarizmi via India, and in use by 10th century Abu'l-Hasan al-Uqlidisi
Abu'l-Hasan al-Uqlidisi
Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
and 15th century Jamshīd al-Kāshī
Jamshid al-Kashi
Ghiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
's work "Arithematic Key".
Addition
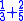
- Put the two numerators 1,2 on the left side of counting board, put the two denominators 3 and 5 at the right hand side
- Cross multiply 1 with 5, 2 with 3 to get 5 and 6, replace the numerators with the corresponding cross products.
- Multiply the two denominators 3 and 5 =15, put at bottom right
- Add the two numerators 5 and 6=11 put on top right of counting board.
- Result
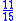
Subtraction
- Put down the rod numeral for numerators 1 and 8 at left hand side of a counting board
- Put down the rods for denomintors 5 and 9 at the right hand side of a counting board
- Cross multiply 1 x9=9, 5x8=40, replace the corresponding numerators
- Multiply the denominators 5 x 9=45, put 45 at the bottom right of counting board, replace the denominator 5
- Subtract 40-9=31, put on top right.
- Result
=
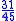
Multiplication
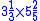
- Arrange the counting rods for
and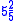 
on the counting board as shang,shi,fa tabulation format. - shang times fa add to shi: 3*3+1=10； 5*5+2=27
- shi multiplied by shi：10*27=270
- fa multiplied by fa：3*5=15
- shi divided by fa:
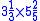=18
Hightest common factor and fraction reduction
The algorithm for finding the hightst common factor of two numbers and reduction offraction was laid out in Jiuzhang suanshu.
The highest common factor is found by successive division with remainders until
the last two remainders are identical.
The animation on the right illustrates the algorithm for finding the hightest common factor of
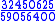and reduction of a fraction.In this case the hcf is 25.
Divide the numerator and denominator by 25.The reduced fraction is
.Interpolation
Calendarist and mathematician He Chengtian used fraction interpolation method, called "harmonization of the divisor of the day" to obtain a better approximate value than the old one by iteratively adding the numerators and denominators a "weaker" fraction with a "stronger fraction". Zu ChongzhiZu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
's legendary π=
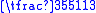could be obtained with He Chengtian's methodSystem of linear equations
Jiuzhang suanshu provided algorithm for solving System of linear equations:Problem 8-1: Suppose we have 3 bundles of top quality cereals, 2 bundles of medium quality cereals and a bundle of low quality cereal, total thirty nine dou. We also have 2, 3 bundles and 1 bundle of respective cereals amount to 34 dou; we also have 1,2 and 3 bundles of respective cereals, total 26 dou.
Find the quantity of top, medium, and poor quality cereals.
In algebra, this problem can be expressed in three system equation with three unknowns.
-
-
-
- 3x+2Y+z=39
- 2x+3y+z=34
- x+2y+3z=26
-
-
This problem was solved in Jiuzhang suanshu with counting rods laid out on counting board in a tabular format similar to a 3x4 matrix:
| quality | left column | center column | right column |
| top | |
 |
 |
| medium |  |
 |
|
| low | |
|
|
| shi | |
|
 |
Algorithm:
- Multiply the center column with right column top quality number.
- Repeatedly subtract right column from center column, until the top number of center column =0
- multiply the left column with the value of top row of right column
- Repeatedly subtract right column from left column, until the top number of left column=0
- After applying above elimination algorithm to the reduced center column and left column, the matrix was reduced to triangular shape:
quality left column center column right column top medium 
low shi
The amount of on bundle of low quality cereal =
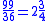
From which the amount of one bundle of top and medium quality cereals can be found easily:
One bundle of top quality cereals=9 dou
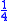
One bundle of medium cereal=4 dou
>Extraction of Square root
Algorithm for extraction of square root was described in Jiuzhang suanshu and with minor difference in terminology in The Mathematical Classic of Sun ZiThe Mathematical Classic of Sun Zi
The Mathematical Classic of Sun Zi was a mathematical treatise written during the 5th century, and was listed as one of The Ten Computational Canons in Tang Dynasty. The identity of the author Sunzi is still unknown, and not to be confused with the author of The Art of War...
.
The animation shows the algorithm for rod calculus extraction of an approximation of the square root
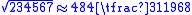from the algorithm in chap 2 problem 19 of The Mathematical Classic of Sun Zi:
- Now there is a square area 234567, find one side of the square.
The algorithm is as follows:
- Set up 234567 on the counting board, on the second row from top, named shi
- Set up a marker 1 at 10000 position at the 4th row named xia fa
- Estimate the first digit of square root to be counting rod numeral 4, put on the top row (shang) hundreds position,
- Multiply the shang 4 with xiafa 1, put the product 4 on 3rd row named fang fa
- Multiply shang with fang fa deduct the product 4x4=16 from shi: 23-16=7, remain numeral 7.
- double up the fang fa 4 to become 8, shift one position right, and change the vertical 8 into horizontal 8 after moved right.
- Move xia fa two position right.
- Estimate second digit of shang as 8: put numeral 8 at tenth position on top row.
- Multiply xia fa with the new digit of shang, add to fang fa
.
- 8 calls 8 =64, subract 64 from top row numeral "74", leaving one rod at the most significant digit.
- double the last digit of fang fa 8, add to 80 =96
- Move fang fa96 one position right, change convention;move xia fa "1" two position right.
- Estimate 3rd digit of shang to be 4.
- Multiply new digit of shang 4 with xia fa 1, combined with fang fa to make 964.
- subtract successively 4*9=36,4*6=24,4*4=16 from the shi, leaving 311
- double the last digit 4 of fang fa into 8 and merge with fang fa
- result
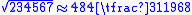
North Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
developed addtive multiplicative algorithm for extration square root, in which he replaced the traditional "doubling" of "fang fa" by adding
shang digit to fang fa digit, with same effect.
Extraction of cubic root
Jiuzhang suanshu vol iv "shaoguang" provided algorithm for extraction of cubic root.〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何？答曰：一百二十三尺。
problem 19: We have a 1860867 cubic chi, what is the length of a side ? Answer:123 chi.
North Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
invented a method similar to simplified form of Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
for extraction of cubic root.
The animation at right shows Jia Xian's algorithm for solving problem 19 in Jiuzhang suanshu vol 4.
Polynomial equation
North Song dynasty mathematician Jia XianJia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
invented Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
for solving simple 4th order equation of the form
South Song dynasty mathematician Qin Jiushao improved Jia Xian's Horner method to solve polynomial equation up to 10th order.
The following is algorithm for solving
-
-
-
-
-
-
-
-
-
-
-
-
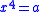in his Mathematical Treatise in Nine SectionsMathematical Treatise in Nine SectionsThe Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
vol 6 problem 2.
-
-
-
-
-
-
-
-
-
-
-
This equation was arranged bottom up with counting rods on counting board in tabular form