
Counting rods
Encyclopedia
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
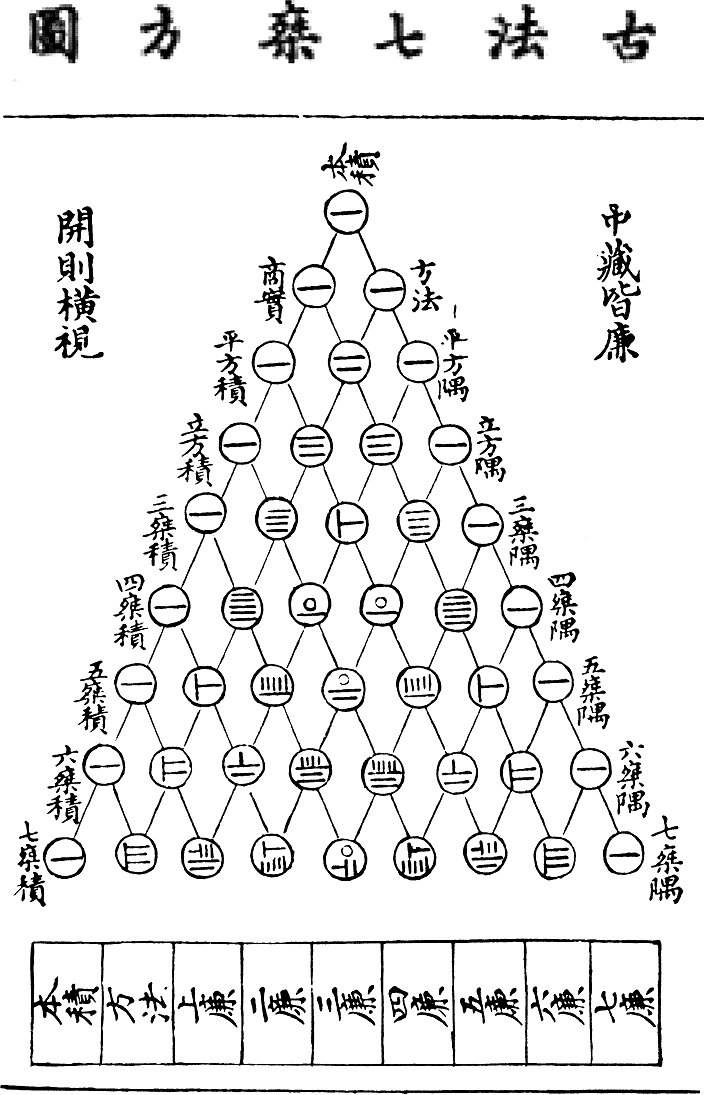
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
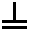 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
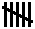 |
 |
 |
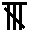 |
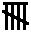 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
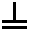 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
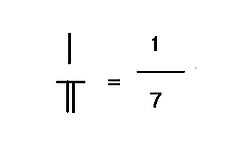
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
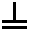 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
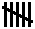 |
 |
 |
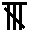 |
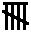 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
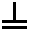 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
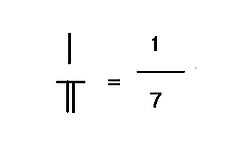
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
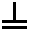 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
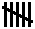 |
 |
 |
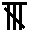 |
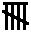 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
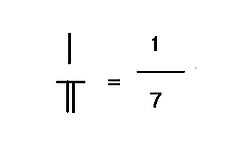
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
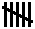 |
 |
 |
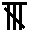 |
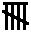 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
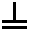 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
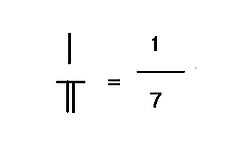
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
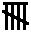 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
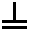 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
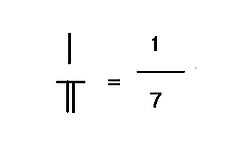
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
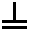 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
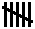 |
 |
 |
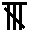 |
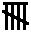 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
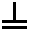 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
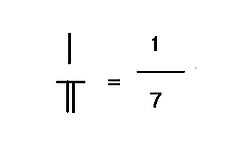
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
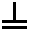 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
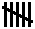 |
 |
 |
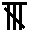 |
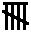 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
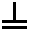 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
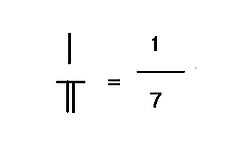
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
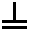 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
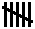 |
 |
 |
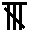 |
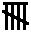 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
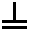 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
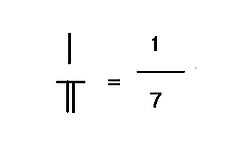
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007

China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
, Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
, Korea
Korea
Korea ) is an East Asian geographic region that is currently divided into two separate sovereign states — North Korea and South Korea. Located on the Korean Peninsula, Korea is bordered by the People's Republic of China to the northwest, Russia to the northeast, and is separated from Japan to the...
, and Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
. They are placed either horizontally or vertically to represent any number and any fraction.
The written forms based on them are called rod numerals. They are a true positional numeral system with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
for 1-9 and a blank for 0 , since Warring states to 16th century.
History
Counting rods were used by ancient Chinese for more than two thousand years. In 1954, forty-odd counting rods of the Warring States PeriodWarring States Period
The Warring States Period , also known as the Era of Warring States, or the Warring Kingdoms period, covers the Iron Age period from about 475 BC to the reunification of China under the Qin Dynasty in 221 BC...
were found in Zuǒjiāgōngshān (左家公山) Chǔ
Chu (state)
The State of Chu was a Zhou Dynasty vassal state in present-day central and southern China during the Spring and Autumn period and Warring States Period . Its ruling house had the surname Nai , and clan name Yan , later evolved to surname Mi , and clan name Xiong...
Grave No.15 in Changsha, Hunan
Hunan
' is a province of South-Central China, located to the south of the middle reaches of the Yangtze River and south of Lake Dongting...
..
In 1973, archeologists unearthed a number of wood scripts from a Han dynasty tomb in Hubei, one of the wooden script written:“当利二月定算
 ”,this is one of the earliest examples of using counting rod numeral in writing.
”,this is one of the earliest examples of using counting rod numeral in writing.In 1976, a bundle of West Han counting rods made of bones in was unearthed from Qian yang county in Shanxi The use of counting rods must predate it; the Laozi
Laozi
Laozi was a mystic philosopher of ancient China, best known as the author of the Tao Te Ching . His association with the Tao Te Ching has led him to be traditionally considered the founder of Taoism...
, a text originating from the Warring States, said "a good calculator doesn't use counting rods." The Book of Han
Book of Han
The Book of Han, Hanshu or History of the Former Han Dynasty |Fan Ye]] . Various scholars have estimated that the earliest material covered in the book dates back to between 206 and 202 BCE...
recorded: "they calculate with bamboo, diameter one fen, length six cun, arranged into a hexagonal bundle of two hundred seventy one pieces."
After the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
flourished, counting rods were abandoned except in Japan, where rod numerals developed into symbolic notation for algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Using counting rods

Sun Tzu (mathematician)
Sun Tzu or Sun Zi was a Chinese mathematician, flourishing between the 3rd and the 5th century AD.Interested in astronomy and trying to develop a calendar, he investigated Diophantine equations...
wrote that "one is vertical, ten is horizontal."
Red rods represent positive numbers and black rods represent negative numbers. Ancient Chinese clearly understood negative numbers and zero (leaving a blank space for it), though they had no symbol for the latter. The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, which was mainly composed in the first century CE, stated "(when using subtraction) subtract same signed numbers, add different signed numbers, subtract a positive number from zero to make a negative number, and subtract a negative number from zero to make a positive number." Later, a go stone was sometimes used to represent 0.
This alternation of vertical and horizontal rod numeral form is very important to correctly understand written trascription of rod numerals on manuscripts. For instance, in Licheng suanjin, 81 was transribed as
 , and 108 was transribed as
, and 108 was transribed as 
 ; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as
; it is clear that the latter clearly had a blank zero on the "counting board" (ie, floor or mat), even though on the written transcription, there was no blank. In the same manuscript, 405 was transcribed as 
 , with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
, with a blank space in between for obvious reasons, and could in no way be interpreted as "45"
 . In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional.
. In other words, transcribed rod numerals may not be positional, but on the counting board, they are positional. 
 is an exact image of the counting rod number 405 on a table top or floor.
is an exact image of the counting rod number 405 on a table top or floor.Place value
The value of a number depends on its physical position on the counting board; a 9 at the rightmost position on the board stands for 9, move the batch of rods representing 9 to the left one position (i.e., the ten position) = 9blanck =90, shift left three position = 9[][] = 900; and so on. Similariy, move a number right each rank tantamount to divide the number by 10. This applies to single-digit number or multiple digit number.Song dynasty mathematician Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
used hand-written Chinese decimal orders 步十百千万 as rod numeral place value, as evident from a facsimile from a page of Yongle Encyclopedia
Yongle Encyclopedia
The Yongle Encyclopedia was a Chinese compilation of information commissioned by the Chinese Ming Dynasty emperor Yongle in 1403 and completed by 1408...
. He arranged 七万一千八百二十四 as
-
-
-
-
-
-
-
-
-
-
-
- 七一八二四
- 万千百十步
-
-
-
-
-
-
-
-
-
-
He treated the Chinese order numbers as place value markers, and 七一八二四 became place value decimal number. He then wrote the rod numerals according to their place value:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
 |
 |
 |
 |
 |
In Japan, mathematicians put counting rods on a counting board, a sheet of cloth with grids, and used only vertical forms relying on the grids. An 18th-century Japanese mathematics book has a checker counting board diagram, with the order of magnitude symbols "千百十一分厘毛“(myriad, hundred, ten, unit, one tenth, etc)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical | ||||||||||
| Horizontal |
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Horizontal |  |
 |
 |
 |
 |
 |
Examples:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| -407 |  |
 |
||
| -6720 |  |
 |
 |
Rod numerals
Rod numerals are a positional numeral system made from shapes of counting rods. Positive numbers are written as they are and the negative numbers are written with a slant bar at the last digit. The vertical bar in the horizontal forms 6-9 is drawn shorter to have the same character height.A circle (〇) is used for 0. Many historians think it was imported from Indian numerals
Indian numerals
Most of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
by Gautama Siddha
Gautama Siddha
Gautama Siddha, astronomer, astrologer and compiler of Indian descent, known for leading the compilation of the Treatise on Astrology of the Kaiyuan Era during the Tang Dynasty. He was born in Chang'an, and his family was originally from India, according to a tomb stele uncovered in 1977 in Xi'an...
in 718, but some think it was created from the Chinese text space filler "□".
In the 13th century, Southern Song
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
mathematicians changed digits for 4, 5, and 9 to reduce strokes. The new horizontal forms eventually transformed into Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
. Japanese continued to use the traditional forms.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Horizontal |  |
 |
 |
 |
 |
 |
 |
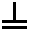 |
 |
 |
| -0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
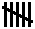 |
 |
 |
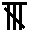 |
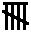 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Vertical |  |
 |
 |
 |
 |
 |
 |
|||
| Horizontal |  |
 |
 |
 |
 |
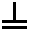 |
 |
Examples:
| Traditional | Southern Song | |
|---|---|---|
| 231 |    |
   |
| 5089 |     |
  |
| -407 |    |
  |
| -6720 |     |
    |
In Japan, Seki Takakazu
Seki Takakazu
, also known as , was a Japanese mathematician in the Edo period.Seki laid foundations for the subsequent development of Japanese mathematics known as wasan; and he has been described as Japan's "Newton."...
developed the rod numerals into symbolic notation for algebra and drastically improved Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. After his period, the positional numeral system using Chinese numeral characters was invented, and the rod numerals worked only as the plus and minus signs
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
.
| Western | Seki | After Seki |
|---|---|---|
| x + y + 246 |  甲 甲 乙 乙   |
 甲 甲 乙 乙 二四六 二四六 |
| 5x - 6y |  甲 甲 乙 乙 |
 五甲 五甲 六乙 六乙 |
| 7xy |  甲乙 d 甲乙 d |
 七甲乙 七甲乙 |
| 8x / y | N/A | 乙 八甲 八甲 |
Fractions
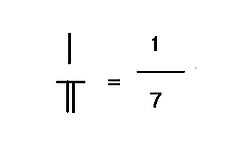
Rod calculus
The method for using counting rods for mathematical calculation was called rod calculation or rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
(筹算). Rod calculus can be used for a wide range of calculations, including finding the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, finding square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, cube roots, or higher order roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
, and solving a system of linear equations. As a result, the character 籌 is extended to connote the concept of planning in Chinese. For example, the science of using counting rods 運籌學 does not refer to counting rods; it means operational research.
Before the introduction of written zero, there was no way to separate 10007 and 107 in written forms except by inserting a bigger space between 1 and 7, and so rod numerals were used only for doing calculations with counting rods. Once written zero came into play, the rod numerals had become independent, and their use indeed outlives the counting rods, after its replacement by abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
One variation of horizontal rod numerals, the Suzhou numerals
Suzhou numerals
The Suzhou numerals or huama is a numeral system used in China before the introduction of Arabic numerals.-History:The Suzhou numeral system is the only surviving variation of the rod numeral system. The rod numeral system is a positional numeral system used by the Chinese in mathematics...
is still in use for book-keeping and in herbal medicine prescription in Chinatown
Chinatown
A Chinatown is an ethnic enclave of overseas Chinese people, although it is often generalized to include various Southeast Asian people. Chinatowns exist throughout the world, including East Asia, Southeast Asia, the Americas, Australasia, and Europe. Binondo's Chinatown located in Manila,...
s in some parts of the world.
Counting rods in Unicode
UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
5.0 includes counting rod numerals in their own block in the Supplementary Multilingual Plane (SMP) from U+1D360 to U+1D37F. The code points for the horizontal digits 1-9 are U+1D360 to U+1D368 and those for the vertical digits 1-9 are U+1D369 to U+1D371. The former are called unit digits and the latter are called tens digits, which is opposite of the convention described above. Zero should be represented by U+3007 (〇, ideographic number zero) and the negative sign should be represented by U+20E5 (combining reverse solidus overlay). As these were recently added to the character set and since they are included in the SMP, font support may still be limited. Grey areas indicate non-assigned code points.
See also
- Rod calculusRod calculusRod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
- AbacusAbacusThe abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
- Chinese mathematicsChinese mathematicsMathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
- Unicode numeralsUnicode numeralsNumerals are characters that denote a number. The same Arabic-Indic numerals are used widely in various writing systems throughout the world and all share the same semantics for denoting numbers, However, the graphemes representing these numerals differ widely from one writing system to another...
- Tian yuan shuTian yuan shu' is a Chinese system of algebra for polynomial equations created in the 13th century. It is first known from the writing of Li Zhi , though it was created earlier....
External links
For a look of the ancient counting rods, and further explanation, you can visit the sites- The Development of Hindu Arabic and Traditional Chinese Arithematics
- http://www.math.sfu.ca/histmath/China/Beginning/Rod.html
- http://mathforum.org/library/drmath/view/52557.html

