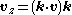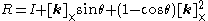
Rodrigues' rotation formula
Encyclopedia
In the theory of three-dimensional rotation, Rodrigues' rotation formula (named after Olinde Rodrigues
) is an efficient algorithm for rotating a vector in space, given an axis
and angle of rotation
. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation. In other words, the Rodrigues formula provides an algorithm to compute the exponential map
from so(3) to SO(3) without computing the full matrix exponent.
If v is a vector in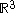 and k is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense
and k is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense
), the Rodrigues formula is:
Olinde Rodrigues
Benjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
) is an efficient algorithm for rotating a vector in space, given an axis
Axis angle
The axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
and angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation. In other words, the Rodrigues formula provides an algorithm to compute the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
from so(3) to SO(3) without computing the full matrix exponent.
If v is a vector in
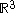 and k is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed sense
and k is a unit vector describing an axis of rotation about which we want to rotate v by an angle θ (in a right-handed senseRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
), the Rodrigues formula is:
-
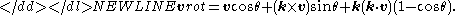
Derivation
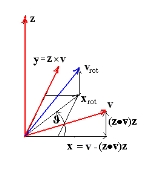
Given a rotation axis z represented by a unit vector k = (kX, kY, kZ), and a vector v = (vX, vY, vZ) that we wish to rotate about z, the vector
is the component of v parallel to z, also called the vector projection of v on k, and the vector
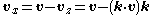
is the projection of v onto the xy plane orthogonal to z, also called the vector rejection of v from k.
Notice that we chose to define a reference frameReference frameReference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...
xyz in which the z axis is aligned with the rotation axis, and the x axis with the rejection of v from k. This simplifies the demonstration, as it implies that v lies on the xz plane, and its component vy is null (see figure). However, xyz does not coincide with the reference frame XYZ in which vectors v, k, vx, and vz are actually represented. For instance, v = (vX, vY, vZ) ≠ (vx, vy, vz). In other words, Rodrigues' formula is independent of the orientation in spaceOrientation (geometry)In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of the reference frame XYZ in which v and k are represented.
Next let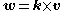 .
.
Notice that vx and w have the same length. By definition of the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, the length of w is: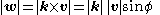
where Φ denotes the angle between z and v.
Since k has unit length,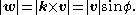
This coincides with the length of vx, computed trigonometrically as follows: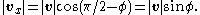
So w can be viewed as a copy of vx rotated by 90° about z. Using trigonometry, we can now rotate vx by θ around z to obtain vx rot. Its two components with respect of x and y are vxcosθ and wsinθ, respectively. Thus,
-
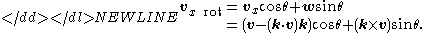
vx rot can be also described as the projection on xy (or rejection from z) of the rotated vector vrot (see figure). Since vz is obviously not affected by a rotation about z, the other component of vrot (i.e. its projection on z) coincides with vz. Thus,-
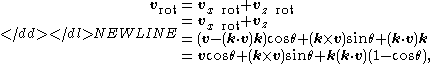
as required.
Matrix notation
By representing v and k as column matrices, and defining a matrix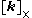 as the "cross-product
as the "cross-product
matrix" for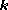 , i.e.,
, i.e.,
-
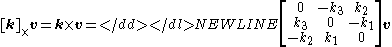 ,
,
Rodrigues' formula can be written in matrix notation:
-
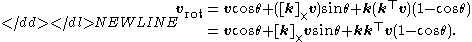
Using the triple product expansion in can be written as:-
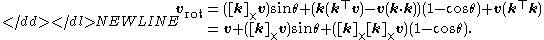
since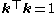 for a normalized vector.
for a normalized vector.
Conversion to rotation matrix
The equation can be also written as-
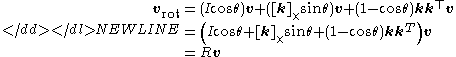
where I is the 3×3 identity matrix. Thus we have a formula for the rotation matrix R corresponding to an axis angleAxis angleThe axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
representation [k θ]:-
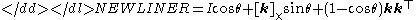 .
.
Noting that, using the outer product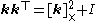 , we have
, we have
or, equivalently,-
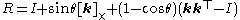 .
.
For the inverse mapping, see Log map from SO(3) to so(3).
See also
- Axis angleAxis angleThe axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
- Rotation (mathematics)Rotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
- SO(3) and SO(4)SO(4)In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO. The name comes from the fact that it is the special orthogonal group of order 4....
- History of quaternionsHistory of quaternionsIn mathematics, quaternions are a non-commutative number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton...
External links
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- For a proof that begins with the xyz frame see http://myyn.org/m/article/proof-of-rodrigues-rotation-formula/
- For another descriptive example see http://chrishecker.com/Rigid_Body_Dynamics#Physics_Articles, Chris Hecker, physics section, part 4. "The Third Dimension" -- on page 3, section ``Axis and Angle, http://chrishecker.com/images/b/bb/Gdmphys4.pdf
- Matthew T. Mason, Representing rotation.
-
-
-
-
-
-
-
-