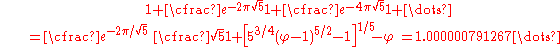Rogers–Ramanujan continued fraction
Encyclopedia
The Rogers–Ramanujan continued fraction is a continued fraction
discovered by and later studied by Srinivasa Ramanujan
, closely related to the Rogers-Ramanujan identities
, that can be evaluated explicitly for special values of its argument.
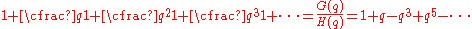
where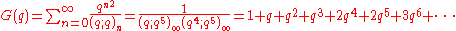
and
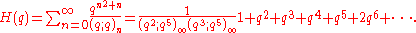
are the functions appearing in the Rogers-Ramanujan identities.
Here,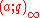
denotes the infinite q-Pochhammer symbol.
implies that their values for τ an imaginary quadratic irrational are algebraic number
s that can be evaluated explicitly. In particular Ramanujan's continued fraction can be evaluated for these values of τ.
where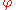
is the golden ratio
(Approximately 1.618)
The multiplicative inverse of this expression is:
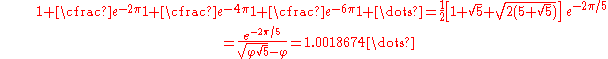
The multiplicative inverse of this expression is:
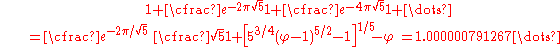
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
discovered by and later studied by Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
, closely related to the Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
, that can be evaluated explicitly for special values of its argument.
Definition
Ramanujan's continued fraction is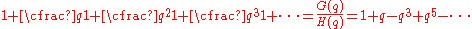 where
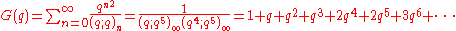
and
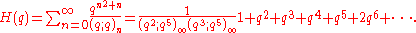
are the functions appearing in the Rogers-Ramanujan identities.
Here,
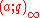denotes the infinite q-Pochhammer symbol.Modular functions
If q = e2πiτ, then q−1/60G(q) and q11/60H(q) and therefore q1/5H(q)/G(q)) are modular functions of τ. Since they have integral coefficients, the theory of complex multiplicationComplex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
implies that their values for τ an imaginary quadratic irrational are algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s that can be evaluated explicitly. In particular Ramanujan's continued fraction can be evaluated for these values of τ.
Examples
where
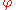is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(Approximately 1.618)
The multiplicative inverse of this expression is:
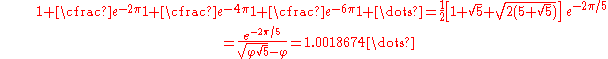
The multiplicative inverse of this expression is: