Rouché's theorem
Encyclopedia
Rouché's theorem, named after , states that if the complex
-valued functions
f and g are holomorphic
inside and on some closed contour K, with |g(z)| < |f(z)| on K, then f and f + g have the same number of zeros inside K, where each zero is counted as many times as its multiplicity. This theorem assumes that the contour K is simple, that is, without self-intersections.
(1902–1991) proved in his book Complex Numbers and Functions the following relation: Let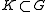
be a bounded region with continuous boundary 
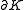. Two holomorphic functions 
have the same number of roots in 
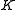, if the strict inequality
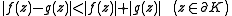
holds on the boundary
.
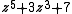has exactly 5 zeros in the disk 
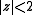since 
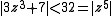for every 
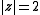, and 
, the dominating part, has five zeros in the disk.
It is possible to provide an informal explanation of Rouche's theorem.
First we need to slightly rephrase the theorem. Let h(z) = f(z) + g(z). If f and g are both holomorphic, then h must also be holomorphic. Then, with the conditions imposed above, the Rouche's theorem in its original (and not symmetric) form says that
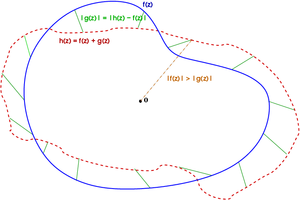
Notice that the condition |f(z)| > |h(z) − f(z)| means that for any z, the distance from f(z) to the origin is larger than the length of h(z) − f(z), which in the following picture means that for each point on the blue curve, the segment joining it to the origin is larger than the green segment associated with it. Informally we can say that the blue curve f(z) is always closer to the red curve h(z) than it is to the origin.
The previous paragraph shows that h(z) must wind around the origin exactly as many times as f(z). The index of both curves around zero is therefore the same, so by the argument principle
, f(z) and h(z) must have the same number of zeros inside C.
One popular, informal way to summarize this argument is as follows: If a person were to walk a dog on a leash around and around a tree, and if the length of the leash is less than the minimum radius of the walk, then the person and the dog go around the tree an equal number of times. (Indeed, one may see that the converse of Rouche's theorem is false, insofar as the leash need only be less than the minimum circumference of the walk.)
. Let
and choose
and so large that:
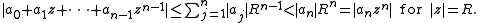
Since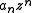
has 
zeros inside the disk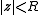 
(because 
), it follows from Rouché's theorem that 
also has the same number of zeros inside the disk.
One advantage of this proof over the others is that it shows not only that a polynomial must have a zero but the number of its zeros is equal to its degree (counting, as usual, multiplicity).
Another use of Rouché's theorem is to prove the open mapping theorem
for analytic functions. We refer to the article for the proof.
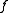and 
do not have any roots on the boundary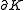 
and that 
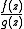is not a negative real number for 
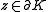. Thus the homotopy
is well defined for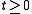
, where 
.
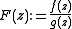Clearly,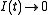
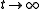as 
. As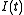 
is continuous and integer valued, it follows that 
.
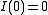By the argument principle
, this winding number is given by
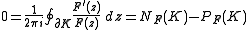
where NF(K) is the number of zeroes of F inside K, PF(K) is the number of poles inside K. Hence NF = PF. But F is the ratio of two holomorphic functions f and g inside K, and so the zeroes are those of f and the poles are the zeros of g (at least if f and g are coprime polynomials, which we can assume since otherwise, we are free to divide f and g by any common divisor). That is,
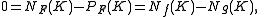
as required.
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f and g are holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
inside and on some closed contour K, with |g(z)| < |f(z)| on K, then f and f + g have the same number of zeros inside K, where each zero is counted as many times as its multiplicity. This theorem assumes that the contour K is simple, that is, without self-intersections.
Symmetric version
Theodor EstermannTheodor Estermann
Theodor Estermann was a mathematician, working in the field of analytic number theory.He was born in Neubrandenburg, Germany. His doctorate, completed in 1925, was supervised by Hans Rademacher. Heini Halberstam, Klaus Roth and Robert Charles Vaughan were Ph.D. students of his.-External links:*...
(1902–1991) proved in his book Complex Numbers and Functions the following relation: Let
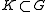be a bounded region with continuous boundary 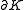. Two holomorphic functions have the same number of roots in 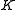, if the strict inequality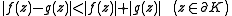holds on the boundary
.Usage
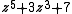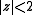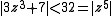The theorem is usually used to simplify the problem of locating zeros, as follows. Given an analytic function, we write it as the sum of two parts, one of which is simpler and grows faster than (thus dominates) the other part. We can then locate the zeros by looking at only the dominating part. For example, the polynomial has exactly 5 zeros in the disk since for every 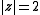, and , the dominating part, has five zeros in the disk.Geometric explanation
First we need to slightly rephrase the theorem. Let h(z) = f(z) + g(z). If f and g are both holomorphic, then h must also be holomorphic. Then, with the conditions imposed above, the Rouche's theorem in its original (and not symmetric) form says that
- If |f(z)| > |h(z) − f(z)| then f(z) and h(z) have the same number of zeros in the interior of C.
Notice that the condition |f(z)| > |h(z) − f(z)| means that for any z, the distance from f(z) to the origin is larger than the length of h(z) − f(z), which in the following picture means that for each point on the blue curve, the segment joining it to the origin is larger than the green segment associated with it. Informally we can say that the blue curve f(z) is always closer to the red curve h(z) than it is to the origin.
The previous paragraph shows that h(z) must wind around the origin exactly as many times as f(z). The index of both curves around zero is therefore the same, so by the argument principle
Argument principle
In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
, f(z) and h(z) must have the same number of zeros inside C.
One popular, informal way to summarize this argument is as follows: If a person were to walk a dog on a leash around and around a tree, and if the length of the leash is less than the minimum radius of the walk, then the person and the dog go around the tree an equal number of times. (Indeed, one may see that the converse of Rouche's theorem is false, insofar as the leash need only be less than the minimum circumference of the walk.)
Applications
Rouché's theorem can be used to give a short proof of the Fundamental Theorem of AlgebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. Let
and choose
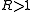and so large that: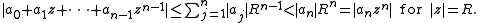Since
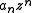has zeros inside the disk 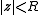(because ), it follows from Rouché's theorem that also has the same number of zeros inside the disk.One advantage of this proof over the others is that it shows not only that a polynomial must have a zero but the number of its zeros is equal to its degree (counting, as usual, multiplicity).
Another use of Rouché's theorem is to prove the open mapping theorem
Open mapping theorem (complex analysis)
In complex analysis, the open mapping theorem states that if U is a connected open subset of the complex plane C and f : U → C is a non-constant holomorphic function, then f is an open map .The open mapping theorem points to the sharp difference between holomorphy and real-differentiability...
for analytic functions. We refer to the article for the proof.
Proof of symmetric form of Rouché's theorem
The hypothesis ensures both that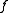 and do not have any roots on the boundary 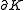and that 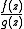is not a negative real number for 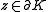. Thus the homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
is well defined for
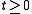, where 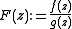.Clearly,
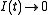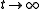as . As 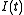is continuous and integer valued, it follows that 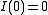.By the argument principle
Argument principle
In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
, this winding number is given by
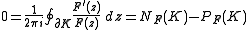
where NF(K) is the number of zeroes of F inside K, PF(K) is the number of poles inside K. Hence NF = PF. But F is the ratio of two holomorphic functions f and g inside K, and so the zeroes are those of f and the poles are the zeros of g (at least if f and g are coprime polynomials, which we can assume since otherwise, we are free to divide f and g by any common divisor). That is,
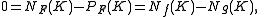
as required.
See also
- Hurwitz's theorem (complex analysis)Hurwitz's theorem (complex analysis)In complex analysis, a field within mathematics, Hurwitz's theorem, named after Adolf Hurwitz, roughly states that, under certain conditions, if a sequence of holomorphic functions converges uniformly to a holomorphic function on compact sets, then after a while those functions and the limit...
- Sturm's theoremSturm's theoremIn mathematics, Sturm's theorem is a symbolic procedure to determine the number of distinct real roots of a polynomial. It was named for Jacques Charles François Sturm...
- Rational root theorem
- Properties of polynomial roots