
Rule 184
Encyclopedia

Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
rule, notable for solving the majority problem
Majority problem (cellular automaton)
The majority problem, or density classification task is the problem of finding one-dimensional cellular automaton rules that accurately perform majority voting.Using local transition rules, cells cannot know the total count of all the ones in system...
as well as for its ability to simultaneously describe several, seemingly quite different, particle system
Particle system
The term particle system refers to a computer graphics technique to simulate certain fuzzy phenomena, which are otherwise very hard to reproduce with conventional rendering techniques...
s:
- Rule 184 can be used as a simple model for traffic flowTraffic flowTraffic flow, in mathematics and civil engineering, is the study of interactions between vehicles, drivers, and infrastructure , with the aim of understanding and developing an optimal road network with efficient movement of traffic and minimal traffic congestion problems.-History:Attempts to...
in a single lane of a highway, and forms the basis for many cellular automaton models of traffic flowMicroscopic traffic flow modelMicroscopic traffic flow models are a class of scientific models of vehicular traffic dynamics.In contrast to macroscopic models, microscopic traffic flow models simulate single vehicle-driver units, thus the dynamic variables of the models represent microscopic properties like the position and...
with greater sophistication. In this model, particles (representing vehicles) move in a single direction, stopping and starting depending on the cars in front of them. The number of particles remains unchanged throughout the simulation. Because of this application, Rule 184 is sometimes called the "traffic rule". - Rule 184 also models a form of depositionDeposition (Aerosol physics)In aerosol physics, Deposition is the process by which aerosol particles collect or deposit themselves on solid surfaces, decreasing the concentration of the particles in the air. It can be divided into two sub-processes: dry and wet deposition. The rate of deposition, or the deposition velocity,...
of particles onto an irregular surface, in which each local minimum of the surface is filled with a particle in each step. At each step of the simulation, the number of particles increases. Once placed, a particle never moves. - Rule 184 can be understood in terms of ballistic annihilation, a system of particles moving both leftwards and rightwards through a one-dimensional medium. When two such particles collide, they annihilate each other, so that at each step the number of particles remains unchanged or decreases.
The apparent contradiction between these descriptions is resolved by different ways of corresponding features of the automaton's state with particles. The name of the rule is a Wolfram code
Wolfram code
Wolfram code is a naming system often used for one-dimensional cellular automaton rules, introduced by Stephen Wolfram in a 1983 paper and used in his book A New Kind of Science....
that defines the evolution of its states. The earliest research on Rule 184 seems to be the papers by Li (1987) and Krug and Spohn (1988). In particular, Krug and Spohn already describe all three types of particle system modeled by Rule 184.
Definition
A state of the Rule 184 automaton consists of a one-dimensional array of cells, each containing a binary valueBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
(0 or 1). In each step of its evolution, the Rule 184 automaton applies the following rule to each of the cells in the array, simultaneously for all cells, to determine the new state of the cell:
| current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| new state for center cell | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
An entry in this table defines the new state of each cell as a function of the previous state and the previous values of the neighboring cells on either side.
The name for this rule, Rule 184, is the Wolfram code
Wolfram code
Wolfram code is a naming system often used for one-dimensional cellular automaton rules, introduced by Stephen Wolfram in a 1983 paper and used in his book A New Kind of Science....
describing the state table above: the bottom row of the table, 10111000, when viewed as a binary number, is equal to the decimal number 184
184 (number)
184 is the natural number following 183 and preceding 185.-In mathematics:* 184 is an even number* 184 is a composite number* 184 is a deficient number, as 176 is less than 184...
.
The rule set for Rule 184 may also be described intuitively, in several different ways:
- At each step, whenever there exists in the current state a 1 immediately followed by a 0, these two symbols swap places. Based on this description, Krug and Spohn (1984) call Rule 184 a deterministic version of a "kinetic Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
with asymmetric spin-exchange dynamics". - At each step, if a cell with value 1 has a cell with value 0 immediately to its right, the 1 moves rightwards leaving a 0 behind. A 1 with another 1 to its right remains in place, while a 0 that does not have a 1 to its left stays a 0. This description is most apt for the application to traffic flow modeling.
- If a cell has state 0, its new state is taken from the cell to its left. Otherwise, its new state is taken from the cell to its right. That is, each cell can be implemented by a multiplexerMultiplexerIn electronics, a multiplexer is a device that selects one of several analog or digital input signals and forwards the selected input into a single line. A multiplexer of 2n inputs has n select lines, which are used to select which input line to send to the output...
, and is closely related in its operation to a Fredkin gateFredkin gateThe Fredkin gate is a computational circuit suitable for reversible computing, invented by Ed Fredkin. It is universal, which means that any logical or arithmetic operation can be constructed entirely of Fredkin gates...
.
Dynamics and majority classification
From the descriptions of the rules above, two important properties of its dynamics may immediately be seen. First, in Rule 184, for any finite set of cells with periodic boundary conditionsPeriodic boundary conditions
In mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
, the number of 1s and the number of 0s in a pattern remains invariant throughout the pattern's evolution. Similarly, if the density of 1s is well-defined for an infinite array of cells, it remains invariant as the automaton carries out its steps. And second, although Rule 184 is not symmetric under left-right reversal, it does have a different symmetry: reversing left and right and at the same time swapping the roles of the 0 and 1 symbols produces a cellular automaton with the same update rule.
Patterns in Rule 184 typically quickly stabilize, either to a pattern in which the cell states move in lockstep one position leftwards at each step, or to a pattern that moves one position rightwards at each step. Specifically, if the initial density of cells with state 1 is less than 50%, the pattern stabilizes into clusters of cells in state 1, spaced two units apart, with the clusters separated by blocks of cells in state 0. Patterns of this type move rightwards. If, on the other hand, the initial density is greater than 50%, the pattern stabilizes into clusters of cells in state 0, spaced two units apart, with the clusters separated by blocks of cells in state 1, and patterns of this type move leftwards. If the density is exactly 50%, the initial pattern stabilizes (more slowly) to a pattern that can equivalently be viewed as moving either leftwards or rightwards at each step: an alternating sequence of 0s and 1s.
One can view Rule 184 as solving the majority problem
Majority problem (cellular automaton)
The majority problem, or density classification task is the problem of finding one-dimensional cellular automaton rules that accurately perform majority voting.Using local transition rules, cells cannot know the total count of all the ones in system...
, of constructing a cellular automaton that can determine whether an initial configuration has a majority of its cells active: if Rule 184 is run on a finite set of cells with periodic boundary conditions, and the number of active cells is less than half of all cells, then each cell will eventually see two consecutive zero states infinitely often, and two consecutive one states only finitely often, while if the number of active cells forms a majority of the cells then each cell will eventually see two consecutive ones infinitely often and two consecutive zeros only finitely often. The majority problem cannot be solved perfectly if it is required that all cells eventually stabilize to the majority state but the Rule 184 solution avoids this impossibility result by relaxing the criterion by which the automaton recognizes a majority.
Traffic flow

Traffic wave
Traffic waves, also called stop waves or traffic shocks, are travelling disturbances in the distribution of cars on a highway. Traffic waves usually travel backwards in relation to the motion of the cars themselves, or "upstream". The waves can also travel downstream, however, more commonly become...
when it is heavy.
It is difficult to pinpoint the first use of Rule 184 for traffic flow simulation, in part because the focus of research in this area has been less on achieving the greatest level of mathematical abstraction and more on verisimilitude: even the earlier papers on cellular automaton based traffic flow simulation typically make the model more complex in order to more accurately simulate real traffic. Nevertheless, Rule 184 is fundamental to traffic simulation by cellular automata. Wang et al. (1997), for instance, state that "the basic cellular automaton model describing a one-dimensional traffic flow problem is rule 184." Nagel (1996) writes "Much work using CA models for traffic is based on this model." Several authors describe one-dimensional models with vehicles moving at multiple speeds; such models degenerate to Rule 184 in the single-speed case. Gaylord and Nishidate (1996) extend the Rule 184 dynamics to two-lane highway traffic with lane changes; their model shares with Rule 184 the property that it is symmetric under simultaneous left-right and 0-1 reversal. Biham et al. (1992) describe a two-dimensional city grid model
Biham-Middleton-Levine traffic model
The Biham-Middleton-Levine traffic model is a self-organizing cellular automaton traffic flow model. It consists of a number of cars represented by points on a lattice with a random starting position, where each car may be one of two types: those that only move downwards , and those that only move...
in which the dynamics of individual lanes of traffic is essentially that of Rule 184. For an in-depth survey of cellular automaton traffic modeling and associated statistical mechanics, see Chowdhury et al. (2000).
When viewing Rule 184 as a traffic model, it is natural to consider the average speed of the vehicles. When the density of traffic is less than 50%, this average speed is simply one unit of distance per unit of time: after the system stabilizes, no car ever slows. However, when the density is a number ρ greater than 1/2, the average speed of traffic is
 . Thus, the system exhibits a second-order kinetic phase transition
. Thus, the system exhibits a second-order kinetic phase transitionPhase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
at ρ = 1/2. At that critical value the average speed approaches its stationary limit as the square root of the number of steps, while away from the critical value the approach is exponential.
Surface deposition
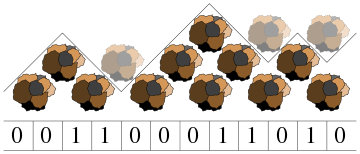
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
oriented diagonally. If a particle is present at some position of the lattice, the lattice positions below and to the right, and below and to the left of the particle must also be filled. At each time step, the surface grows by the deposition of particles in each local minimum of the surface; that is, at each position where it is possible to add a new particle. To model this process by Rule 184, we observe that the boundary between filled and unfilled lattice positions can be marked by a polygonal line, the segments of which separate adjacent lattice positions and have slopes +1 and -1. We model a segment with slope +1 by an automaton cell with state 0, and a segment with slope -1 by an automaton cell with state 1. The local minima of the surface are the points where a segment of slope -1 lies to the left of a segment of slope +1; that is, in the automaton, a position where a cell with state 1 lies to the left of a cell with state 0. Adding a particle to that position corresponds to changing the states of these two adjacent cells from 1,0 to 0,1, which is exactly the behavior of Rule 184.
Related work on this model concerns deposition in which the arrival times of additional particles are random, rather than having particles arrive at all local minima simultaneously. These stochastic growth processes can be modeled as an asynchronous cellular automaton
Asynchronous cellular automaton
Cellular automata, as with other multi-agent system models, usually treat time as discrete and state updates as occurring synchronously. The state of every cell in the model is updated together, before any of the new states influence other cells...
.
Ballistic annihilation

Antiparticle
Corresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
s annihilate each other when they collide. In the simplest version of this process, the system consists of a single type of particle and antiparticle, moving at equal speeds in opposite directions in a one-dimensional medium.
This process can be modeled by Rule 184, as follows. We view the particles as aligned, not with the cells of the automaton, but rather with the interstices between cells. If two consecutive cells both have state 0, we view the transition between them as forming a particle that moves rightwards one cell at each time step. If, on the other hand, two consecutive cells both have state 1, we view the transition between them as forming an antiparticle that moves leftwards one cell at each time step. Two consecutive cells with differing states are considered to form part of a background material without any particles in it. It may be observed that these particles interact by ballistic annihilation: when a rightwards-moving particle and a leftwards-moving antiparticle meet, the result is a region of background from which both particles have vanished, without any effect on any other nearby particles.
The behavior of certain other systems, such as one-dimensional cyclic cellular automata, can also be described in terms of ballistic annihilation. There is a technical restriction on the particle positions for the ballistic annihilation view of Rule 184 that does not arise in these other systems, stemming from the alternating pattern of the background: in the particle system corresponding to a Rule 184 state, if two consecutive particles are both of the same type they must be an odd number of cells apart, while if they are of opposite types they must be an even number of cells apart. However this parity restriction does not play a role in the statistical behavior of this system.
Pivato (2005) uses a similar but more complicated particle-system view of Rule 184: he not only views alternating 0-1 regions as background, but also considers regions consisting solely of a single state to be background as well. Based on this view he describes seven different particles formed by boundaries between regions, and classifies their possible interactions. See Chopard and Droz (1998, pp. 188–190) for a more general survey of the physics of annihilation processes.
Context free parsing
In his book A New Kind of ScienceA New Kind of Science
A New Kind of Science is a book by Stephen Wolfram, published in 2002. It contains an empirical and systematic study of computational systems such as cellular automata...
, Stephen Wolfram
Stephen Wolfram
Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
points out that rule 184, when run on patterns with density 50%, can be interpreted as parsing the context free language describing strings formed from nested parentheses
Bracket
Brackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
. This interpretation is closely related to the ballistic annihilation view of rule 184: in Wolfram's interpretation, an open parenthesis corresponds to a left-moving particle while a close parenthesis corresponds to a right-moving particle.
See also
- Biham-Middleton-Levine traffic modelBiham-Middleton-Levine traffic modelThe Biham-Middleton-Levine traffic model is a self-organizing cellular automaton traffic flow model. It consists of a number of cars represented by points on a lattice with a random starting position, where each car may be one of two types: those that only move downwards , and those that only move...
, a two-dimensional analogue of Rule 184. - Microscopic traffic flow model#Cellular automaton models.

