Microscopic traffic flow model
Encyclopedia
Microscopic traffic flow models are a class of scientific models of vehicular traffic dynamics
.
In contrast to macroscopic models, microscopic traffic flow models simulate single vehicle-driver units, thus the dynamic variables of the models represent microscopic properties like the position and velocity of a single vehicle.
and velocities 
. It is assumed that the input stimuli of the drivers are restricted to the own velocity 
, the net distance (bumper-to-bumper distance) 
to the leading vehicle 
(
denotes the vehicle length), and the velocity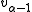 
of the leading vehicle. The equation of motion
of each vehicle is characterized by an acceleration function that depends on those input stimuli:
In general, the driving behavior of a single driver-vehicle unit
might not merely depend on the immediate leader 
but on the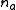 
vehicles in front. The equation of motion in this more generalized form reads:
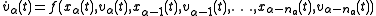
(CA) models are using integer variables to describe the dynamical properties of the system. The road is divided into sections of a certain length
and the time is discretized to steps of 
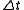. Each road section can either be occupied by a vehicle or empty and the dynamics are given by update rules of the form:
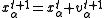
(the simulation time
is measured in units of 
and the vehicle positions 
in units of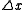 
).
The time scale is typically given by the reaction time of a human driver,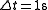
. With 
fixed, the length of the road sections determines the granularity of the model. At a complete standstill, the average road length occupied by one vehicle is approximately 7.5 meters. Setting 
to this value leads to a model where one vehicle always occupies exactly one section of the road and a velocity of 5 corresponds to 
, which is then set to be the maximum velocity a driver wants to drive at. However, in such a model, the smallest possible acceleration would be 
which is unrealistic. Therefore, many modern CA models use a finer spatial discretization, for example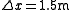 
, leading to a smallest possible acceleration of 
.
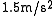Although cellular automaton models lack the accuracy of the time-continuous car-following models, they still have the ability to reproduce a wide range of traffic phaenomena. Due to the simplicity of the models, they are numerically very efficient and can be used to simulate large road networks in realtime or even faster.
Traffic flow
Traffic flow, in mathematics and civil engineering, is the study of interactions between vehicles, drivers, and infrastructure , with the aim of understanding and developing an optimal road network with efficient movement of traffic and minimal traffic congestion problems.-History:Attempts to...
.
In contrast to macroscopic models, microscopic traffic flow models simulate single vehicle-driver units, thus the dynamic variables of the models represent microscopic properties like the position and velocity of a single vehicle.
Car-following models
Also known as time-continuous models, all car-following models have in common that they are defined by ordinary differential equations describing the complete dynamics of the vehicles' positions and velocities . It is assumed that the input stimuli of the drivers are restricted to the own velocity , the net distance (bumper-to-bumper distance) to the leading vehicle ( denotes the vehicle length), and the velocity 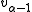of the leading vehicle. The equation of motionEquation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
of each vehicle is characterized by an acceleration function that depends on those input stimuli:
In general, the driving behavior of a single driver-vehicle unit
might not merely depend on the immediate leader but on the 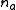vehicles in front. The equation of motion in this more generalized form reads: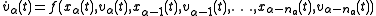Examples of car-following models
- Optimal Velocity Model (OVM)
- Velocity Difference Model (VDIFF)
- Wiedemann ModelVISSIMVISSIM is a microscopic multi-modal traffic flow simulation software. It is developed by PTV Planung Transport Verkehr AG in Karlsruhe, Germany. The name is derived from “Verkehr In Städten - SIMulationsmodell”...
(1974) - Intelligent Driver ModelIntelligent Driver ModelIn traffic flow modeling, the intelligent driver model is a time-continuous car-following model for the simulation of freeway and urban traffic...
(IDM, 1999) - Gipps' ModelGipps' ModelGipps’ Model is a car-following model named after Peter G. Gipps who developed it in the late-1970s under S.R.C. grants at the at the University of Newcastle-Upon-Tyne and the Transport Studies Group at the University College London. It is based directly on driver behavior and expectancy for...
(Gipps, 1981)
Cellular automaton models
Cellular automatonCellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
(CA) models are using integer variables to describe the dynamical properties of the system. The road is divided into sections of a certain length
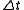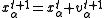
and the time is discretized to steps of . Each road section can either be occupied by a vehicle or empty and the dynamics are given by update rules of the form:(the simulation time
is measured in units of and the vehicle positions in units of 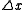).The time scale is typically given by the reaction time of a human driver,
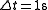. With fixed, the length of the road sections determines the granularity of the model. At a complete standstill, the average road length occupied by one vehicle is approximately 7.5 meters. Setting to this value leads to a model where one vehicle always occupies exactly one section of the road and a velocity of 5 corresponds to , which is then set to be the maximum velocity a driver wants to drive at. However, in such a model, the smallest possible acceleration would be which is unrealistic. Therefore, many modern CA models use a finer spatial discretization, for example 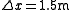, leading to a smallest possible acceleration of 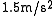.Although cellular automaton models lack the accuracy of the time-continuous car-following models, they still have the ability to reproduce a wide range of traffic phaenomena. Due to the simplicity of the models, they are numerically very efficient and can be used to simulate large road networks in realtime or even faster.
Examples of CA models
- Rule 184Rule 184Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:...
- Biham-Middleton-Levine traffic modelBiham-Middleton-Levine traffic modelThe Biham-Middleton-Levine traffic model is a self-organizing cellular automaton traffic flow model. It consists of a number of cars represented by points on a lattice with a random starting position, where each car may be one of two types: those that only move downwards , and those that only move...
- Nagel-Schreckenberg modelNagel-Schreckenberg modelThe Nagel-Schreckenberg model is a theoretical model for the simulation of freeway traffic. The model was developed in the early 90s by the German physicists Kai Nagel and Michael Schreckenberg...
(NaSch, 1992)